江苏省清江中学2005届高考数学模拟试卷
蔡如森
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间120分钟。
第I卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]() 正棱锥、圆锥的侧面积公式
正棱锥、圆锥的侧面积公式![]() 其中c表示底面周长,l表示斜高或母线长球的体积公式
其中c表示底面周长,l表示斜高或母线长球的体积公式![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、设全集I={1,3,5,7,9},A={1,a-5,9},![]() ={5,7},则a为( )
={5,7},则a为( )
A、2 B、8 C、-2或8 D、2或8
2、∠A是△ABC的一个内角,![]() ,则∠A的取值范围是
( )
,则∠A的取值范围是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、由数字1、2、3、4、5组成的所有没有重复数字的5位数中,是偶数的有( )A、120 B、72 C、48 D、96
4、设一个正多面体的面数为F,顶点数为V,若F+V=8,且它的各条棱长都等于1,则这一多面体的高等于 ( )
A、 ![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、以椭圆![]() 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线![]() 的渐近线相切的圆方程是
(
)
的渐近线相切的圆方程是
(
)
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、我校有50岁以上的老教师40人,35----50岁的中年教师有200人,35岁以下的青年教师80人,为了调查教师们对校教代会制定的一项规章制度的满意度,准备抽出80人进行问卷调查,问中年教师应抽的人数为 ( )
A、10 B、20 C、50 D、80
7、![]() 展开式的第四项等于7,则x等于
( )
展开式的第四项等于7,则x等于
( )
A、-5 B、![]() C、
C、![]() D、5
D、5
8 、已知函数![]() 。则它的反函数
。则它的反函数![]() 是减函数的
是减函数的
充要条件是 ( )
A、1<a<2
B、a>1 C、
0<a<1 D、![]()
9、已知函数f(x)是定义在R上的奇函数,当x<0时,![]() ,则
,则![]() 的值是
( )
的值是
( )
A、-2 B、2
C、![]() D、
D、![]()
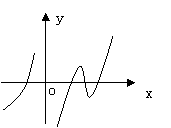
10、设函数f(x)在定义域上存在导数,
y=f(x)的图象如右图所示,则导函数
![]() 的图象可能是 ( )
的图象可能是 ( )
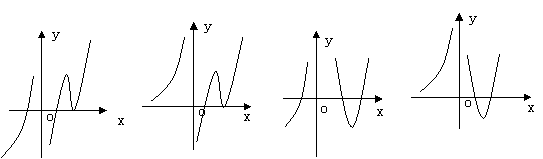
A B C D
11、设函数F(x)=f(x)-f(-x),x∈R,![]() 是函数F(x)的单调递增区间,将F(x)的图象 按
是函数F(x)的单调递增区间,将F(x)的图象 按![]() 平移得到一个新的函数G(x)的图象,则G(x) 的单调递增区间必定是 ( )
平移得到一个新的函数G(x)的图象,则G(x) 的单调递增区间必定是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、假设每一架飞机的引擎在飞行中出现故障率为1-p,且各引擎是否有故障是独立的,如有至少50%的引擎能正常运行,飞机就可成功飞行。若使4引擎飞机比2引擎飞机更为安全,则p的取值范围是 ( )
A、(![]() ) B、(
) B、(![]() ) C、(
) C、(![]() ) D、(
) D、(![]() )
)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13、已知函数![]() 的定义域是[2,8],则函数f(x)的反函数的定义域为
。
的定义域是[2,8],则函数f(x)的反函数的定义域为
。
14、直线l截圆x2+y2-2y=0所得弦AB的中点是(![]() ),则直线l的方
),则直线l的方
程为 ;AB= 。
15、若an=1+2+3+……+n,则数列{![]() }的前n项和Sn=
。
}的前n项和Sn=
。
16、经过△OAB的重心G的直线与OA、OB两边分别交于P、Q,设![]() ,
,![]() 向量,则m+n=
。(写出m、n的关系式)
向量,则m+n=
。(写出m、n的关系式)
三、解答题:本大题共6小题,共74分.解答题应写出文字说明、证明过程或演算步骤.
17、(本小题满分12分)
设y=f(x)是定义在R上的任一函数,求证:(1)F(x)=f(x)-f(-x)为奇函数;G(x)=f(x)+f(-x)为偶函数;(2)请你根据(1)以任一定义在R上的函数为例,构造出一个奇函数和一个偶函数。
18、(本小题满分12分)
假如在2008年的奥运会上中国足球队和美国足球队经过加时赛比分仍为0:0,现决定各派5名队员,每人射一个点球决定胜负,假设两支球队派出的队员每人的点球命中概率均为0.5(相互独立)。
(1)如果不考虑美国足球队,那么中国足球队5名队员中有连续三名队员射中,而另外两名队员未射中的概率是多少?
(2)中国足球队、美国足球队两队各射完5个点球后,再次出现平局的概率是多么?
19、(本小题满分12分)
已知向量![]() ,ω>0,记函数f(x)=
,ω>0,记函数f(x)=![]() ,已知f(x)的最小正周期为
,已知f(x)的最小正周期为![]() .
.
(1)求ω的值;
(2)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时函数f(x)的值域。
20、(本小题满分12分)
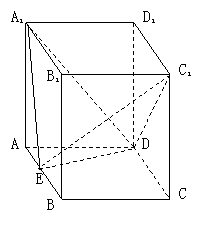 如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
如图:直平行六面体ABCD-A1B1C1D1,底面ABCD是边长为2a的菱形,∠BAD=600,E为AB中点,二面角A1-ED-A为600
(I)求证:平面A1ED⊥平面ABB1A1;
(II)求二面角A1-ED-C1的余弦值;
(III)求点C1到平面A1ED的距离。
21、(本小题满分12分)
设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3,且数列{an+1-an}(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)是否存在k∈N*,使ak-bk∈![]() ?若存在,求出k的值;若不存在,说明理由.
?若存在,求出k的值;若不存在,说明理由.
22、(本小题满分14分)
椭圆E的中心在原点O,焦点在x轴上,离心率![]() ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:![]() (λ≥2)。
(λ≥2)。
(1)若λ为常数,试用直线l的斜率k(k≠0)表示三角形OAB的面积;
(2)若λ为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程;
(3)若λ变化,且λ=k2+1,试问:实数λ和直线l的斜率k(k∈R)分别为何值时,椭圆E的短半轴长取得最大值?并求出此时的椭圆方程。
参考答案
一、选择题:1-5,DBCAA;6-10,CBCBD;11-12,DC
二、填空题:13、[7,68];14、x-y+2=0,![]() ;15、
;15、![]() ;16、3mn;
;16、3mn;
三、解答题:
17、(1)证明:设x为R上的任一实数,
则F(-x)=f(-x)-f(x)=-[f(x)-f(-x)]=- F(x)
所以:F(x)为奇函数;(3分)
设x为R上的任一实数,则G(-x)=f(-x)+f(x)=G(x)
所以:G(x)为偶函数;(6分)
(2)设定义在R上的函数f(x)为f(x)=2x,(8分)
则可构造出奇函数为:F(x)=2x-2-x;(10分)
偶函数为:G(x)=2x+2-x;(12分)
(只要定义域为R的函数均可)
18、解:(1)中国足球队5名队员中有连续三名队员射中,另两名队员未射中有三种情况,故![]() .(5分)
.(5分)
(2)中国足球队、美国足球队两队各射完5个球,再次出现平局可能的情况有6种:①均未中球,②均中1球,③均中2球,④均中3球,⑤均中4球,⑥均中5球,(7分)
故所求概率为:![]() (9分)
(9分)
![]() (11分)
(11分)
答:(1)中国足球队5名队员中有连续三名队员射中,另两名队员未射中的概率为![]() ;(2)中国足球队、美国足球队两队各射完5个球,再次出现平局的的概率为
;(2)中国足球队、美国足球队两队各射完5个球,再次出现平局的的概率为![]() (12分)
(12分)
19、解:(1)∵![]()
∴f(x)=![]() =
=![]() =
=![]()
=![]() =
=![]() (4分)
(4分)
∴周期T=![]() =
=![]() ∴ω=2(6分)
∴ω=2(6分)
(2)由(1)知:![]() (7分)
(7分)
∵b2=ac,∴在△ABC中由余弦定理得:
![]() ≥
≥![]() (9分)
(9分)
又因为余弦函数在[0,π]上是减函数,∴![]() (10分)
(10分)
且![]() (10分)∴
(10分)∴![]()
∴![]() (11分)
(11分)
即:函数f(x)的值域为[![]() ]。(12分)
]。(12分)
20、(I) 证明:连结BD,在菱形ABCD中,∠BAD=600,∴△ABD为正三角形,∵E为AB的中点,∴ED⊥AB (1分)
在直六面体ABCD-A1B1C1D1中:平面ABB1A1⊥平面ABCD且交于AB,∵ED![]() 面ABCD∴ED⊥面ABB1A1 (2分)∴平面A1ED⊥平面ABB1A1
(3分)
面ABCD∴ED⊥面ABB1A1 (2分)∴平面A1ED⊥平面ABB1A1
(3分)
(II)解: 由(I)知:ED⊥面ABB1A1 ∵A1E![]() 面ABB1A1 ∴A1E⊥ED
面ABB1A1 ∴A1E⊥ED
又在直平行六面体ABCD-A1B1C1D1中:AA1⊥面ABCD,由三垂线定理的逆定理知:AE⊥ED,∴∠A1EA=600
(4分)取BB1的中点F,连EF、AB1,则EF![]()
![]() ,在直平行六面体ABCD-A1B1C1D1中:AB1
,在直平行六面体ABCD-A1B1C1D1中:AB1![]() DC1∴EF
DC1∴EF![]()
![]() ∴E、F、C1、D四点共面(5分)∵ED⊥面ABB1A1且EF
∴E、F、C1、D四点共面(5分)∵ED⊥面ABB1A1且EF![]() 面ABB1A1∴EF⊥ED∴∠A1EF为二面角A1-ED-C1的平面角(6分)
面ABB1A1∴EF⊥ED∴∠A1EF为二面角A1-ED-C1的平面角(6分)
在Rt△EBF中:![]() ,
,![]()
在Rt△A1AE中:![]() ,
,
在Rt△A1B1F中:![]() (7分)
(7分)
∴在Rt△A1EF中: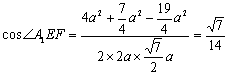
∴二面角A1-ED-C1的余弦值为![]() (8分)
(8分)
(III)过F作FG⊥A1E交A1E于G点∵平面A1ED⊥面ABB1A1
且平面A1ED∩面ABB1A1=A1E∴FG⊥平面A1ED,即:FG是点F到平面A1ED的距离(10分)在Rt△EGF中:![]() ∴
∴![]()
∴![]() (11分)
(11分)
∵EF![]()
![]() 且E、D∈面A1ED∴点C1到平面A1ED的距离为
且E、D∈面A1ED∴点C1到平面A1ED的距离为![]() (12分)
(12分)
21、解:(1)由已知:a2-a1=-2,a3-a2=-1,∴(a3-a2)-(a2-a1)=1
∴an+1-an=(a2-a1)+(n-1)·1=-2+ n-1=n-3
∴当n≥2时,an= (an- an-1)+(an-1- an-2)+……+(a3- a2)+(a2- a1)+a1
=(n-4)+(n-5)+……+(-1)+(-2)+6=![]()
当n=1时也适合∴![]() (n∈N*)(3分)
(n∈N*)(3分)
又b1-2=4,b2-2=2,且![]() ∴bn-2=(b1-2)·
∴bn-2=(b1-2)·![]() 即:bn=2+8
即:bn=2+8![]()
∴数列{an}、{bn}的通项公式分别为:![]() ,
,
bn=2+8![]() (n∈N*)(6分)
(n∈N*)(6分)
(2)设f(k)=ak-bk=![]() (8分)
(8分)
当k≥4时,![]() 为k的增函数,
为k的增函数,![]() 也为k的增函数,
也为k的增函数,
∴当k≥4时f(k)=ak-bk≥f(4)=![]() (10分)
(10分)
又f(1)=f(2)=f(3)=0∴不存在k,使f(k)∈![]() (12分)
(12分)
22设椭圆方程为:![]() (a>b> 0),由
(a>b> 0),由![]() 及a2=b2+c2得a2=3b2,故椭圆方程为x2+3y2=3b2①
及a2=b2+c2得a2=3b2,故椭圆方程为x2+3y2=3b2①
(1)∵直线L:y=k(x+1)交椭圆于A(x1,y1),B(x2,y2)两点,
并且![]() (λ≥2)
(λ≥2)
∴(x1+1,y1)=λ(-1-x2,-y2),即 ②把y=k(x+1)代入椭圆方程,得:(3k2+1)x2+6k2x+3k2-3b2=0,且△=k2(3b2-1)+b2>0,
②把y=k(x+1)代入椭圆方程,得:(3k2+1)x2+6k2x+3k2-3b2=0,且△=k2(3b2-1)+b2>0,
∴![]() ③
③![]() ④
④
∴![]() 联立②、③得:
联立②、③得:![]() ∴
∴![]() (6分)
(6分)
(2)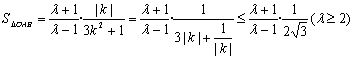 当且仅当
当且仅当![]() 即
即![]() 时,S△OAB取得最大值。此时
时,S△OAB取得最大值。此时![]() ,又∵x1+1=-λ(x2+1),
,又∵x1+1=-λ(x2+1),
∴![]() ,代入④得:
,代入④得:![]() 故此时椭圆的方程为
故此时椭圆的方程为
![]() (10分)
(10分)
(3)由②、③联立得:![]()
![]() 将x1、x2代入④得:
将x1、x2代入④得:![]() 由k2=λ-1
由k2=λ-1
得:![]()
易知:当λ≥2时,3b2是λ的减函数,故当λ=2时,(3b2)max=3.故当λ=2,
k=±1时,椭圆短半轴长取得最大值,此时椭圆方程为x2+3y2=3。(14分)