![]()
高考数学模拟试题
四川省邻水中学(国家级示范高中)特级教师 杨才荣
(总分:150分,考试时间:120分钟)
第Ⅰ卷(选择题 , 共60分)
一、 选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 直线x + 3y-7= 0和kx-y-2 = 0与x轴、y轴的正半轴所围成的四边形有外接圆 , 则k为( )
(A) -3 ( B ) 6 ( C ) -6 ( D ) 3
(2)已知tan(![]() -α) =
-α) = ![]() ,tan(
,tan(![]() -β) =
-β) = ![]() ,则tan(α-β)等于
( )
,则tan(α-β)等于
( )
(A)![]() (B)-
(B)-![]() (C)
(C)![]() (D)-
(D)-![]()
(3)设![]() 、
、![]() 是不共线的单位向量,若
是不共线的单位向量,若![]() = 5
= 5![]() +3
+3![]() ,
,![]() = 3
= 3![]() -5
-5![]() , 则
, 则![]() ⊥
⊥![]() 是
是![]() ⊥
⊥![]() 的 ( )
的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既非充分又非必要条件
(4)已知平面α与平面β相交,直线m⊥α , 则 ( )
(A)β内必存在直线与m平行,且存在直线与m垂直
(B)β内不一定存在直线与m平行,也不一定存在直线与m垂直
(C)β内不一定存在直线与m平行,但必存在直线与m垂直
(D)β内必存在直线与m平行,但不一定存在直线与m垂直
(5)设函数f(x) = 3ax+1-2a
,在区间(-1,1)上存在![]() ,使f(x0) = 0 ,则实数a的取值范围是 ( )
,使f(x0) = 0 ,则实数a的取值范围是 ( )
(A)-1<a<![]() (B)a>
(B)a>![]() (C)a>
(C)a>![]() 或a<-1 (D)a<-1
或a<-1 (D)a<-1![]()
(6)复数Z满足![]() ,则
,则 ![]() 的取值范围是
( )
的取值范围是
( )
(A)![]() (B)
(B)![]() (C)
(C)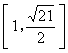 (D)
(D)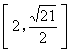
(7) 椭圆![]() (a> b >0) 有内接正n边形 ,则n的可能值是 ( )
(a> b >0) 有内接正n边形 ,则n的可能值是 ( )
(A) 4 (B) 3,4 (C) 3,4,5 (D) 3,4,6
(8)设一个正多面体的面数为F,顶点数为V,若F + V = 8,且它的各条棱长都等于4,则这一多面体的外接球的球面面积是 ( )
(A)12π (B)24π (C)16π (D)28π
(9)数列{an}中,a1 = 1 , 且an+1 = an +![]() +
+![]() ,则a99等于
( )
,则a99等于
( )
(A)2004 (B)2005 (C)2400 (D)2500
(10)曲线C与函数 y = 2x-3 的图象关于直线 l : y = x 对称 ,则曲线 C 与 l 的一个交点的横坐标属于区间 ( )
(A)(-2,-1) (B)(2,3) (C)(1,2) (D)(-1,0)
(11)用四种不同颜色给一正方体的六个表面涂色,相邻两面涂不同颜色,则共有涂色方法有 ( )
(A)24种 (B)72种 (C)96种 (D)48种
(12)在曲线y = x3 + x – 2的切线中,与直线4x –y = 1平行的切线方程是 ( )
(A)4x –y = 0 (B)4x –y – 4 = 0
(C)2x –y – 2 = 0 (D)4x –y – 4 = 0 或 4x –y = 0
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,将答案填写在题中的横线上
(13)设集合A={5,log2(a+3)},集合B={a,b},若A∩B={2},则A∪B = ________________![]()
(14)若不等式![]() <1的解集为{xx<1或x>2=,则实数a的值为________________
<1的解集为{xx<1或x>2=,则实数a的值为________________![]()
(15)曲线![]() 在点(1,3)处的切线方程是
在点(1,3)处的切线方程是
(16) 双曲线![]() 的两个焦点为
的两个焦点为![]() , P是此双曲线上一点,若PF1
, P是此双曲线上一点,若PF1![]() PF2 , 则点P到x轴的距离为_______________.
PF2 , 则点P到x轴的距离为_______________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤
(17)(本小题满分12分)
是否存在常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() 恒成立 , 试证明你的结论。
恒成立 , 试证明你的结论。
(18)(本小题满分12分)
在![]() 中,A、B、C分别为三个内角,a、b、c分别为其对边,
中,A、B、C分别为三个内角,a、b、c分别为其对边,![]() 外接圆半径为
外接圆半径为![]() ,已知
,已知![]()
![]() ;
;
(Ⅰ)求角C ;
(Ⅱ)求![]() 面积S的最大值 .
面积S的最大值 .
(19)(本小题满分12分)
已知正项数列{an}和{bn}中,a1 = a ,(0<a<1=,b1=1-a,当n≥2且n∈![]() 时,an = an-1bn , bn =
时,an = an-1bn , bn =![]() ,
,
(Ⅰ)证明:对任意n∈![]() ,都有an + bn =
1
,都有an + bn =
1
(Ⅱ)求数列 {an} 的通项公式
(Ⅲ)设Cn = a![]() ·bn+1 , Sn为数列 {Cn} 的前n项和,求
·bn+1 , Sn为数列 {Cn} 的前n项和,求![]() Sn
的值
Sn
的值
(20)(本小题满分12分)
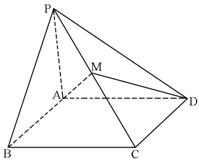
如图,已知四棱锥P-ABCD中,面ABCD为正方形,PA⊥面ABCD,且PA = AB = a ,点M是PC的中点,
(Ⅰ)求异面直线BP与MD所成角的大小;
(Ⅱ)求二面角M-DA-C的大小.
(21)(本小题满分12分)
已知直线l:![]() 与椭圆C:
与椭圆C:![]() ,且b为整数)交于M、N两点,B为椭圆C短轴的上端点,若ΔMBN的重心恰为椭圆焦点F.
,且b为整数)交于M、N两点,B为椭圆C短轴的上端点,若ΔMBN的重心恰为椭圆焦点F.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左焦点为F’,问在椭圆C上是否存在一点P,使得∠F’PF = 60° ,证明你的结论.
(Ⅲ)是否存在斜率不为零的直线l,使椭圆C与直线l相交于不同的两点R、S,且 BR = BS,如果存在,求直线l在y轴上截距的取值范围;如果不存在,请说明理由.
(22)(本小题满分14分)
设x1、x2是函数f(x) = ![]() x3+
x3+![]() x2-a2x
(a>0) 的两个极值点,且x1+x2 = 2
x2-a2x
(a>0) 的两个极值点,且x1+x2 = 2
(Ⅰ)证明:0<a≤1 ;
(Ⅱ)证明:![]() ≤
≤![]() ;
;
(Ⅲ)若函数h(x) = f′(x)-2a(x-x1),证明:当x1<x<2且x1<0时,h(x)≤4a .
参考答案
1、D 2、B 3、C 4、C 5、C 6、B 7、B 8、B 9、D 10、B 11、C 12、D
13、{1,2,5}
14、![]() 15、4x - y – 1 = 0
16、
15、4x - y – 1 = 0
16、![]() .
.
17 证明:当![]() 时,可由已知不等式得出
时,可由已知不等式得出 ![]() 4分
4分
下面分两方面给出证明.
先证![]() ,因为x、y为正数 ,所以
,因为x、y为正数 ,所以
![]()
![]()
![]()
这是显然成立的. 8分
再证![]() 因为
因为![]() x、y为正数,所以
x、y为正数,所以
![]()
![]()
![]()
这是显然成立的.
综上可知,存在常数![]() 使对任何正数
使对任何正数![]() 题中的不等式恒成立. 12分
题中的不等式恒成立. 12分
18 解:(Ⅰ)因为![]() 外接圆半径为
外接圆半径为![]() ,由已知等式和正弦定理得:
,由已知等式和正弦定理得:
![]() ,可化为
,可化为![]() ,结合余弦定理得:
,结合余弦定理得:![]() ,所以
,所以
![]() ,又
,又![]() ,因此
,因此 ![]() .
6分
.
6分
(Ⅱ)由![]() 得
得![]() ,所以
,所以![]()
= ![]() .
.
因此当![]() 时,
时,![]() . 12分
. 12分
19 解:(Ⅰ)用数学归纳法证明
①当n =1时,a1 + b1 = a + (1-a) = 1 , 命题成立;
②假设当n = k (k∈![]() )时命题成立,即ak + bk = 1 , 则当n = k+1时,
)时命题成立,即ak + bk = 1 , 则当n = k+1时,
ak+1+bk+1 =
ak·bk+1+bk+1
= bk+1(1+ak) = ![]() =
= ![]() =
= ![]() = 1
= 1
∴ 当n = k+1时,命题也成立;
综合①②知an+bn=1对n∈![]() 恒成立 4分
恒成立 4分
(Ⅱ)∵ an+1 = an·bn+1 = an·![]() =
= ![]() =
=![]() ,
,
∴ ![]() =
=![]() =
=![]() +1 即
+1 即![]() -
-![]() = 1 (*)
= 1 (*)
∴ 数列{![]() }是公差为1的等差数列,其首项是
}是公差为1的等差数列,其首项是![]() =
=![]()
∴ ![]() =
= ![]() + (n-1)×1,从而an =
+ (n-1)×1,从而an = ![]() 8分
8分
(Ⅲ)∵ Cn
= ![]() = an (an bn+1 ) = an·an+1 ,, ( *) 式变形为an·an+1 = an - an+1 , ∴ Cn = an - an+1
= an (an bn+1 ) = an·an+1 ,, ( *) 式变形为an·an+1 = an - an+1 , ∴ Cn = an - an+1
∴ Sn = C1 + C 2 +
… + Cn = ( a1 - a2 )
+ ( a2 - a3 ) + … + ( an -
an+1 ) = a1 - an+1 = a - ![]() ,
,
∴![]() Sn =
Sn =![]() (a-
(a-![]() ) = a 12分
) = a 12分
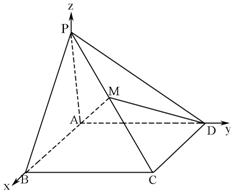
20解法一:
以AB为x轴 ,AD为y轴 ,AP为z轴,建立空间直角坐标系 ,由已知得:
A(0,0,0), B(a , 0 , 0), C( a , a , 0 ) , D( 0 , a , 0 ) , P( 0 , 0 , a ) ,
则PC的中点M的坐标为(![]() ,
,![]() ,
, ![]() ),于是有: 4分
),于是有: 4分
(Ⅰ)设直线PB与DM所成的角为θ , ∵![]() =(-a , 0 , a),
=(-a , 0 , a), ![]() = (
= (![]() , -
, - ![]() ,
, ![]() )
)
∴![]() ·
·![]() = 0 ,∴直线PB与DM所成的角为90° , 8分
= 0 ,∴直线PB与DM所成的角为90° , 8分
(Ⅱ) ∵![]() =(0,0,a)= (a , 0 , 0) ,
=(0,0,a)= (a , 0 , 0) , ![]() = (0 , a , 0) ,
= (0 , a , 0) ,
∴![]() ·
·![]() = 0 ,
= 0 ,![]() ·
·![]() = 0 , ∴ BP与AP的夹角为所求的二面角 ,
10分
= 0 , ∴ BP与AP的夹角为所求的二面角 ,
10分
设BP与AP的夹角为φ,则cosφ = 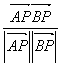 =
= ![]() ,故二面角M-DA-C的大小为45o . 12分
,故二面角M-DA-C的大小为45o . 12分
解法二:
(Ⅰ)取BC的中点N,连接MN、ND,则∠NMD就是异面直线BP与MD所成的角(或其补角),
由PA⊥面ABCD且PA = AB = a , ∴PB = PD = AC = -![]() a ,
PC =
a ,
PC =![]() a , 又M是PC的中点 ,
a , 又M是PC的中点 ,
∴ MN =![]() a ,
MD =
a ,
MD = ![]() a , ND =
a , ND =![]() =
= ![]() a ,
a ,
因此 NM2 + MD2 = ND2 , ∴ ∠MND = 90° .
即异面直线BP与MD所成的角为90° 6分
(Ⅱ)取AC的中点O ,连接MO,则OM∥AP
∵AP⊥面ABCD , ∴OM⊥面ABCD
过O作OR⊥AD交AD于R,连MR,则∠MRO就是二面角M-DA-C的平面角,
∴OM =![]() AP =
AP = ![]() a , OR =
a , OR = ![]() CD =
CD = ![]() a,∴∠MRO = 45°,即二面角M-DA-C的大小为45°
12分
a,∴∠MRO = 45°,即二面角M-DA-C的大小为45°
12分
21解:(Ⅰ)设M、N两点的坐标分别为![]() 、
、![]() ,依题意有
,依题意有
![]() ,由于M、N为直线与椭圆的交点,
,由于M、N为直线与椭圆的交点,
∴![]() ,即18c+5b = 56 ①
,即18c+5b = 56 ①
又 ![]() ②
②
由①、②求得:![]() ,∴椭圆C的方程为
,∴椭圆C的方程为![]() .
4分
.
4分
(Ⅱ) 由(1)知F’与F的坐标分别为(-2,0) 、(2,0) ,设P是椭圆C上任意一点,且![]() ,若
,若![]() ,利用余弦定理及椭圆的定义可得m、n为方程
,利用余弦定理及椭圆的定义可得m、n为方程![]() 的两实根,而此方程无实根
, 所以满足条件的P点不存在. 8分
的两实根,而此方程无实根
, 所以满足条件的P点不存在. 8分
(Ⅲ)假设满足条件的直线l存在,设直线l的方程为![]() ,把
,把![]() 代入椭圆方程并整理得:
代入椭圆方程并整理得:![]() ,则Δ>0,∴
,则Δ>0,∴![]() ①
①
设![]() 为RS的中点,则
为RS的中点,则![]()
∴![]() ,又
,又![]() ∴
∴![]() ,即
,即![]() , ②
, ②
由①、②得![]() ,又
,又![]() ,矛盾,
,矛盾,
故满足条件的直线l不存在. 12分
22 解:(Ⅰ) f′(x) = ax2- bx - a2 , ∵ x1 , x2 是f(x)的两个极值点,
∴x1、x2是方程f′(x) = 0的两个实数根
∵a>0,x1·x2 = -a<0 , x1 + x2 = -![]() ,∴ x1 + x2
= x1-x2 =
,∴ x1 + x2
= x1-x2 =![]() ,
,
∵ x1 + x2
= 2 , ∴ ![]() + 4a = 4 , 即b2 = 4a2-4a3 ,由b2≥0 得 4a2-4a3≥0 , ∴0<a≤1 4分
+ 4a = 4 , 即b2 = 4a2-4a3 ,由b2≥0 得 4a2-4a3≥0 , ∴0<a≤1 4分
(Ⅱ)令 g(a) = 4a2-4a3 , 则g′(a) = 8a-12a2 = 4a ( 2-3a )
由g′(a)>0![]() 0<a<
0<a<![]() , g′(a)<0
, g′(a)<0![]()
![]() <a≤1
<a≤1
故g(a)在区间(0,![]() )上是增函数,在区间(
)上是增函数,在区间(![]() ,1)上是减函数,
,1)上是减函数,
∴g(a)![]() = g(
= g(![]() ) =
) = ![]() ,∴ b ≤
,∴ b ≤![]() 8分
8分
(Ⅲ)∵x1、x2是方程f′(x) = 0的两根,∴ f′(x) = a(x-x1)(x-x2) ,∴ h(x) = a(x-x1)(x-x2)-2a(x-x1)
= a ( x-x1 )( x-x2-2
),∴ h(x) = a x-x1 x-x2-2 ≤a(![]() )2
)2
∵x>x1 , ∴ x-x1 = x-x1 ,又 x1<0 , x1x2<0 , ∴ x2>0 ,∴ x2 + 2>2 ,∵ x<2 , 故x-x2 -2<0 ,
∴ x-x1 + x-x2-2 = x-x1 + x2 + 2-x = x2 - x1 + 2 = x1 + x2 + 2 = 4 ,∴ h(x) ≤4a . 14分