2006年高考数学填空题巧思妙填一点通

填空题是数学高考的三种基本题型之一，其求解方法分为：直接运算推理法、赋值计算法、规律发现法、特值猜想法、数形互助法等等. 在解答问题时，要有合理的分析和判断，要求推理、运算的每一步骤都正确无误，还要求将答案表达得准确、完整. 合情推理、优化思路、少算多思将是快速、准确地解答填空题的基本要求，在草纸上少写一点，在头脑里多思考一点，这可能会加快解的速度. 下面将按知识分类加以例说.

1.　　  函数、不等式与导数

例1（2006年上海春季高考题） 函数的反函数　　　　  ．

　　　 点通：由，得．解出，从而，从而应填.

　　说明：原函数的值域是反函数的定义域．求反函数的程序为：先求原函数的值域，再反解．

例2 　（2006年上海春季高考题）不等式的解集是　　　　　　  ．

　　　 点通：不等式等价于，也就是，所以，从而应填．

说明：快速解答此题需要记住小结论：应用小结论：．

例3 　（2006年上海春季高考题）已知直线过点，且与轴、轴的正半轴分别交于两点，为坐标原点，则三角形面积的最小值为　　　　．

　　　 点通：设直线为，则有关系．

　　对应用２元均值不等式，得，即．

于是，三角形面积为　　．从而应填４．

　　　 说明：也可由，得．特别注意，不等式中的等号是可以成立的．

例4 　（2005年江苏高考试题）已知a,b为常数，若则　　.

点通：由f(x)=x²+4x+3,　 f(ax+b)=x²+10x+24, 得

（ax+b）²+4(ax+b)+3=x²+10x+24,

　　即　　　　a²x²+2abx+b²+4ax+4b+3=x²+10x+24,

  比较系数，得　　　　 

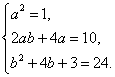
  解得　，　或，所以．

说明：本题考查了复合函数解析式的运用，待定系数法及其相关的计算．

例5　若函数在区间上的最大值和最小值之差为_______．

点通：显然有．易知当时，函数取得最小值；当时，函数取最大值，后者与前者的差为20．

说明：三次函数是高考的一个热门话题．连续函数在闭区间上必有最大值和最小值．

2.　　  三角、向量与复数

例６　已知，且，则________.

点通：由可以读出．而有条件，所以知道，.

说明：记住一些常用的结论，有时可以快速解答问题，如：当时，．看看上面的＂读出＂，“取舍”，“用公式”，想想解题思维的流程，会有什么启发？

例7　复数在复平面内对应的点位于第______象限．

点通：显然有 而由，知道．

说明： 　在解答当中，你能直接看出来吗？复数在高考中是一个淡化的知识点，一般命制一道选择题或填空题．

例８　已知，且其中，则关于的值，在以下四个数值：　　　① 　　　　　　 ②　　　　　　 ③　 　　　　　 ④

其中，的值可以是________．

　  点通：由题意知，从而.此时有

即有于是，排除①和②，应该填③，④．

说明：应用范围估计，有时可以巧妙的解答一些选择或填空题．试问：你有这样的解题经验吗？知识积累（量的增加）的过程也就是能力逐渐提升（质的变化）的过程．

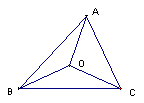例９　 如图，设点O在内部，且有，则的面积与的面积的比为________．

点通：由条件得知，所以点O是AC边上的中线的中点，于是，则的面积与的面积之比为2．

说明：我们知道，等底等高的三角形，其面积相等；共底三角形的面积之比，等于该底上对应高的比．

3.　　  数列、排列组合、二项式定理与概率统计

例10 已知是公差不为零的等差数列，如果是的前n项和，那么

　　点通：　特别取，有，于是有

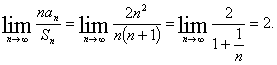　　　　　　　　故应填2.

　　说明：有时，选择特殊的数值、函数、数列、图形等，可快速解答某写填空题，这点应引起读者的重视．

例11 （2005年福建高考题）若常数b满足b>1，则　　　　.

点通：一般解答：

=．

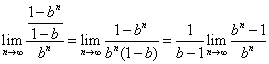简便解答：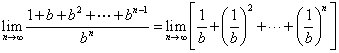

　　　　　　　　　　　　　　　　．

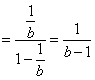说明：比较两个解答，你能想到什么？看来，活学活用是应时时提倡的．

例12 （2005年辽宁高考试题）用１、２、３、４、５、６、７、８组成没有重复数字的八位数，要求１与２相邻，３与４相邻，５与６相邻，而７与８不相邻，这样的八位数共有___________个．（用数字作答）

点通：将１与２，３与４，５与６捆绑在一起排成一列有种，再将７、８插入4个空位中的两个有种，故有种．

说明：相邻用捆绑法，不相邻用插空法．

例13　二项展开式的各项系数的绝对值之和为７２９，则展开式中的常数项是　　　 ．

点通：二项展开式的各项系数的绝对值之和就是展开式的各项系数之和，取，得，则有，所以．于是的通项为

　　　　　　　　　．

　　　　　　　令，得．所以常数项为．

说明：只要细心计算，就不难得出正确的答案．当中的转化你能想的到吗？请多思考，多体会．

例14　如图是一个边长为4的正方形及其内切圆，若随机向正方形内丢一粒豆子，则豆

　　子落入圆内的概率是________．

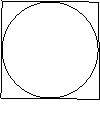点通：因为正方形的面积是１６，内切圆的面积是，所以豆子落入圆内的概率是．

　 说明：概率是高中的新知识，学习时应当紧扣课本的概念，透彻地理解概念的本质，这样就能快速解答问题．

4. 立体几何

　　例15  三棱柱的体积为１，P为侧棱上的一点，则四棱锥的体积为____________．

　　点通：设点P到面ABC，面的距离分别为，则棱柱的高为，又记，则三棱柱的体积为．而从三棱柱中取去四棱锥的剩余体积为

　　　　　，

从而　　

　　说明：立几试题的解答常用到几何体的割与补法，这种分与合思想需要我们反复的琢磨和体味．

例16　 正三棱锥P－ABC的底面边长为1，E、F、G、H分别是PA、 AC、BC、PB的中点，四边形EFGH的面积为S，则S的取值范围是　　　　　　 ．

点通：由题意可知，因而四边形为矩形．设正三棱锥的侧棱，设在平面上的射影为，连，则，从而．故应填．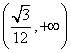

说明：显然，点P到平面ABC的距离可以无限大，这时S也可以无限大．该问题可以在课本上找到它的影子，你知道吗？数学学习请别远离课本，因为有些考题的生长点就在课本上的．

５．解析几何

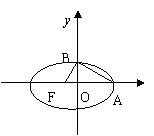例17　 如图，椭圆中心在坐标原点，F为左焦点，当⊥时，

x

其离心率为，此类椭圆被称为“黄金椭圆”．类比黄金椭圆，

可推算出“黄金双曲线”的离心率e 等于_____________ ．

点通：猜想出“黄金双曲线”的离心率e 等于．事实上

　　　　　对直角应用勾股定理，得　，即有

　　　　　　　，

注意到，变形得　，从而

　　说明：类比推理、类比发现是今年高考的一个新的亮点．这种问题的情景比较清新，结构比较巧妙，变化比较合理，是用＂活题＂考能力的典范．

例18 （2005年重庆高考试题）连接抛物线上任意四点组成的四边形可能是　　　　 （填写所有正确选项的序号）．

　　　 ①菱形　　　　　　　　　　 ②有3条边相等的四边形　　　　　　　③梯形

　　　 ④平行四边形　　　　　 ⑤有一组对角相等的四边形

点通：①菱形不可能．如果这个四边形是菱形，那么菱形的一条对角线垂直抛物线的对称轴，这时四边形的必有一个顶点在抛物线的对称轴上(非抛物线的顶点)；④平行四边形也不可能．因为抛物上四个点组成的四边形最多有一组对边平行．故连接抛物线上任意四点组成的四边形可能是②③⑤．

说明：针对②③⑤，你能构造出具体的图形吗？　

6．综合创新题

　　例19　有些计算机对表达式的运算处理过程实行“后缀表达式”：运算符号紧跟在运算对象的后面，按照从左到右的顺序运算，如表达式，其运算为：，若计算机进行运算：，那么使此表达式有意义的的范围为 _____________ ．

　　点通：计算机进行运算：时，它表示的表达式是，当其有意义时，得，解得．

说明：解答问题的关键是：仔细地阅读问题，深刻的理解题意，在此基础上，准确的写出所叙运算的表示式．

　　例20　某种汽车安全行驶的稳定性系数μ随使用年数t的变化规律是μ＝μ₀e^－λt，其中μ₀、λ是正常数．经检测，当t＝2时，μ＝0.09μ₀，则当稳定系数降为0.50μ₀时，该种汽车的使用年数为　　 (结果精确到1，参考数据：lg2＝0.3010，lg3＝0.4771)．

　 点通：由0.90μ₀＝μ₀(e^－λ)²，得e^－λ＝，于是

0.50μ₀＝μ₀(e^－λ)^t()^t，

两边取常用对数，lg，

解出　　　　　　t＝＝13.1．

　　　 说明：　对一个等式的两边取对数，平方，取倒数，移项，等等细小的技巧我们可要熟滥于心呀．这种细节有时可能是解题思维受阻的关节所在．难怪说：成在细节，败也在细节．

　  例21 在某电视歌曲大奖赛中，最有六位选手争夺一个特别奖，观众A，B，C，D猜测如下：A说：获奖的不是1号就是2号；A说：获奖的不可能是3号；C说：4号、5号、6号都不可能获奖；D说：获奖的是4号、5号、6号中的一个．比赛结果表明，四个人中恰好有一个人猜对，则猜对者一定是观众　　　 获特别奖的是　 号选手．

点通：推理如下：因为只有一人猜对，而C与D互相否定，故C、D中一人猜对。假设D对，则推出B也对，与题设矛盾，故D猜错，所以猜对者一定是C；于是B一定猜错，故获奖者是3号选手（此时A错）．

说明：逻辑推理问题是很有趣的，它以能力立意，着力考查思维的灵活性、方向性、选择性和目的性．

填空题的类型一般可分为：完形填空题、多选填空题、条件与结论开放的填空题. 这说明了填空题是数学高考命题改革的试验田，创新型的填空题将会不断出现. 因此，我们在备考时，既要把关注这一新动向，又要做好应试的技能准备.

练习题

１．在下列函数中，满足函数方程的一个函数是________．

２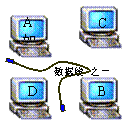．已知正数满足，则的最大值是_________．

３．如图，要用三根数据线将四台电脑A、B、C、D连接　

起来以实现资源共享，则不同的连接方案共有　  　　 种(用数字作答)．　

４．有两个同心圆，在外圆周上有不重合的4个点，在内圆周

上有不重合的2个点，由这6个点确定的直线的条数最少为_____．

　　　 ５．对于函数,我们把使的实数叫做函数的零点．如果函数在区间上的图象是连续不断的一条曲线,并且有，那么,我们就说函数在区间内有零点．则函数的零点有 　 个．　　

　　６．把一张长方形纸片按如图所示的方式连续对折，使每一次得到的折痕保持平行，这样对折7次后展开，问：长方形纸片中有_______条折痕．

第一次对折后　　　　　　　　　　　　　第二次对折后

7. 在平面几何中：ΔABC的∠C内角平分线CE分AB所成线段的比为．把这个结论类比到空间：在三棱锥A—BCD中（如图）DEC平分二面角A—CD—B且与AB相交于E，则得到类比的结论是　　　　　  .

　　　　　　　　　　　　 

８．（2006年上海春季高考题）同学们都知道，在一次考试后，如果按顺序去掉一些高分，那么班级的平均分将降低；反之，如果按顺序去掉一些低分，那么班级的平均分将提高. 这两个事实可以用数学语言描述为：若有限数列 满足，则　　　　　　　　　　　　　　　　　　 

（结论用数学式子表示）．

　　　

答案　１．．　２．１．　３．１６．　４．８．　５．１．　６．127．　

７．．８．，与

．