2006年高考新方案名校难点互动达标提高测试卷

　　　　　　　　  数 学　　　  2006.4

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），共150分，考试时间120分钟。

第Ⅰ卷（选择题　共60分）

一、选择题：本大题共12小题，每小题5分，共计60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知p :不等式 x – 1 + x + 2 > m的解集为R，q : f (x) = log_{5 – 2m}x为减函数，则p是q成立的 （　 ）

　　　 A．充分不必要条件　　　　　　　　　　　　B．必要不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　D．既不充分也不必要条件

2．（理）当z =时，z¹⁰⁰ + z⁵⁰ + 1的值等于 （　 ）

　　　 A．1　　　　　　　　　　B．– 1　　　　　　　　　C．i　　　　　　　　　　　　　　D．– i

　（文）已知全集U = {1，2，3，4，5，6，7}，A = {3，4，5}，B = {1，3，6}，则A∩(_UB) 等于 （　 ）

　　　 A．{4，5}　　　　　　B．{2，4，5，7} C．{1，6}　　　　　　D．{3}

3．函数y = x² – 1 (x < 0)的反函数是 （　 ）

　　　 A．y =（x < – 1）　　　　　　　　　B．y = –（x < – 1）

　　　 C．y =（x > – 1）　　　　　　　　　D．y = –（x > – 1）

4．函数f (x) =的图像相邻的两条对称轴之间的距离是 （　 ）

　　　 A．　　　　　　　　B．5　　　　　　　　 C．　　　　　　　　D．

5．设等差数列{a_n}的前n项和为S_n，且a₃ + a₅ + a₇ = 15，则S₉等于 （　 ）

　　　 A．18　　　　　　　　　B．36　　　　　　　　　 C．45　　　　　　　　　D．60

6．已知P是以F₁、F₂为焦点的椭圆(a > b > 0)上的一点，若= 0，tan∠PF₁F₂ =，则此椭圆的离心率为 （　 ）

　　　 A．　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　 D．

7．（理）、为两个确定的相交平面，a、b为一对异面直线，下列条件中能使a、b所成的角为定值的有 （　　）

　（1）a∥，b　　　　　　　（2）a⊥，b∥　　　　　 （3）a⊥，b⊥

　（4）a∥，b∥，且a与的距离等于b与的距离

　　　 A．0个　　　　　　　　B．1个　　　　　　　　C．2个　　　　　　　　D．4个

　 （文）已知直线l、m、n及平面、，下列命题中的假命题是 （　 ）

　　　 A．若l∥m，m∥n，则l∥n　　　　　B．若l⊥，n∥，则l⊥n

　　　 C．若l∥，n∥，则l∥n　　　　 D．若l⊥，∥，则l⊥

8．将边长为1的正方形ABCD沿对角线BD折起，使得点A到点的位置，且C = 1，则折起后二面角– DC – B的大小为 （　 ）

　　　 A．arctan　　　　　　 B．　　　　　　　　　C．arctan　　　　　　 D．

9．一个三位数，其十位上的数字既小于百位上的数字也小于个位上的数字共有（　 ）

　　　 A．240个　　　　　　B．249个　　　　　　C．285个　　　　　　D．330个

10．盒中有10只螺丝钉，其中有3只是坏的，现从盒中随机地抽取4只螺丝钉，那么等于 （　 ）

　　　 A．恰有1只是坏的概率　　　　　　　　 B．4只全是好的概率

　　　 C．恰有2只是坏的概率　　　　　　　　 D．至多2只是坏的概率

11．（理）函数f (x)的定义域为R，导函数的

图像如图1所示，则函数f (x) （　 ）

　　　 A．无极大值点，有四个极小值点

　　　 B．有三个极大值点，两个极小值点

　　　 C．有两个极大值点，两个极小值点

　　　 D．有四个极大值点，无极小值点

　 （文）已知f (x) = x³ – ax，x∈R，在x = 2处的

切线垂直于直线x + 9y – 1 = 0，　　 则a =（　 ）

　　　 A．1　　　　　　　　　　B．– 1 　　　　　　　　C．3　　　　　　　　　　D．– 3

12．正实数x₁、x₂及函数f (x)满足4^x =且f (x₁) + f (x₂) = 1，则f (x₁ + x₂)的最小值为 （　 ）

　　　 A．4　　　　　　　　　　B．2　　　　　　　　　　C．　　　　　　　　　D．

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上．

13．（理）若n∈N^*，n < 100，且二项式的展开式中存在常数项，则所有满足条件的n值的和是________．

　 （文）在的展开式中常数项是_________．

14．若直线y = 2x + m – 4按向量a =（– 1，2）平移后得到的直线被圆x² + y² = m²截得的弦长为2，则实数m的值为__________．

15．直三棱柱ABC – A₁B₁C₁的每一个顶点都在同一球面上，若AC =，BC = CC₁ = 1，∠ACB =，则A、C两点之间的球面距离为___________．

16．用一批长为2.5m的条形钢材截成长为60cm和43cm的两种规格的零件毛坯，若要使余下的废料最少，则材料的利用率是_______

三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．

17．（本小题满分12分）

　　　 已知函数f (x) = sin．

　 （1）求f (x)的最小正周期；

　 （2）求f (x)的最小值及此时x的值；

　 （3）（理）若当x∈时，f (x)的反函数为f ^{– 1}(x)，求f ^{– 1} (1)的值．

　 （文）求f (x)的单调递增区间．

18．（本小题满分12分）

　 （理）从5名女生和2名男生中任选3人参加英语演讲比赛，设随机变量表示所选3人中男生的人数．

　 （1）求的分布列；

　 （2）求的数学期望；

　 （3）求“所选3人中男生人数≤1”的概率．

　 （文）一名学生在军训中练习射击项目，他射击一次，命中目标的概率是，若连续射击6次，且各次射击是否命中目标相互之间没有影响．

　 （1）求这名学生在第3次射击时，首次命中目标的概率；

　 （2）求这名学生在射击过程中，恰好命中目标3次的概率．

19．（本小题满分12分）

　　　 已知各项均为正数的数列{a_n}前n项和为S_n，(p – 1)S_n = p² – a_n，n∈N^*，p > 0且p≠1，数列{b_n}满足b_n = 2log_pa_n．

　 （1）求a_n，b_n；

　 （2）（只理科做）若p =，设数列的前n项和为T_n，求证：0 < T_n≤4；

　 （3）是否存在自然数M，使得当n > M时，a_n > 1恒成立？若存在，求出相应的M；若不存在，请说明理由．

20．（本小题满分12分）

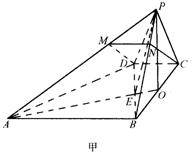
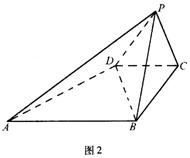　　　 如图2所示，已知四棱锥P–ABCD的底面是直角梯形，∠ABC=∠BCD = 90°，AB = BC = PB = PC = 2CD，侧面PBC⊥底面ABCD．

　 （1）证明：PA⊥BD；

　 （2）求二面角P – BD – C的大小；

　 （3）求证：平面PAD⊥平面PAB．

21．（本小题满分12分）

　　　 已知动点P与双曲线的两个焦点F₁，F₂的距离之和为定值2a (a >)，且向量与夹角的最小值为arccos．

　 （1）求动点P的轨迹方程；

　 （2）过点C (0，1)的直线l交点P的轨迹方程于A、B两点，求的取值范围．

22．（本小题满分14分）

　 （理）对于在区间[m，n]上有意义的两个函数f (x)与g (x)，如果对任意x∈[m，n]均有 f (x) – g (x) ≤1，则称f (x)与g (x)在[m，n]上是接近的，否则称f (x)与g (x)在[m，n]上是非接近的，现有两个函数f ₁(x) = log_a(x – 3a)与f ₂ (x) = log_a(a > 0，a≠1)，给定区间[a + 2，a + 3]．

　 （1）若f ₁(x)与f ₂ (x)在给定区间[a + 2，a + 3]上都有意义，求a的取值范围；

　 （2）讨论f ₁(x)与f ₂ (x)在给定区间[a + 2，a + 3]上是否是接近的？

　 （文）已知函数f (x) = ax² + bx + c (a > b > c)的图像上有两点A (m₁，f (m₁))、B (m₂，f (m₂))，满足f (1) = 0且a² + [f (m₁) + f (m₂)] · a + f (m₁) · f (m₂) = 0．

　 （1）求证：b≥0；

　 （2）求证：f (x)的图像被x轴所截得的线段长的取值范围是；

　 （3）问能否得出f (m₁ + 3)、f (m₂ + 3)中至少有一个为正数？请证明你的结论．

数学参考答案

一、选择题

1．B　p : m < 3　q : 0 < 5 – 2m < 1得2 < m <

　　　 ∵

∴p是q成立的必要不充分条件．

2．（理）D　∵(1 – i)² = – 2i

∴z² = – i，∴z¹⁰⁰ + z⁵⁰ + 1 = ( – i)⁵⁰ + (– i)²⁵ + 1 = – 1 – i + 1 = – i．

  （文）A　_UB = {2，4，5，7}，A∩(_UB) = {4，5}．

3．D　显然y = x² – 1 (x < 0)的值域为(– 1，+)

∴反函数为y =．

4．D　f (x) =cos+ sin

　　　　　　　　= 2(sincos+ cossin)

　　　　　　　　= 2sin

　　　 ∴周期为T =

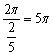
　　　 则相邻的对称轴间的距离为．

5．C　∵a₃ + a₅ + a₇ = 3a₅ = 3 (a₁ + 4d) = 15

而S₉ =× 9 = 9 (a₁ + 4d)

∴

即S₉ = 45．

6．D　由知PF₁⊥PF₂

　　　 ∴

　　　 又知tan∠PF₁F₂ =

∴

而PF₁ + PF₂ = 2a，F₁F₂ = 2c

e =．

7．（理）B　由题意知（3）满足条件，∴有一个．

  （文）C　l和n可满足平行、相交、垂直等多种情况．

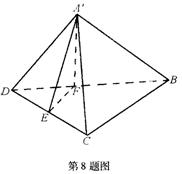8．C　将BD折起后，如图所示作⊥CD于E，作EF∥BC，连，

∵EF⊥CD

又∵⊥CD，则∠F为所求

∵= 1，又= CD = 1

∴=

又E为CD中点，又EF∥BC

∴EFBC，∴EF =，又∵== 1

∴⊥BD，∴=

又+ EF² =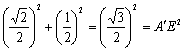

∴⊥EF，∴tan∠．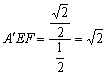

9．C　当十位数取0时，百位数与个位数有种取法，当十位数取1时，百位数与个位数有种取法…，当十位数取8时，百位数与个位数有种取法，∴十位数既小于百位数又小于个位数的三位数共有，1² + 2² + … + 9² =（个）．

10．C　恰有1只坏的概率为P₁ =，4个全是好的概率为P₂ ==，恰有2只坏的概率为P₃ =，至多2只坏的概率P₄ =．

11．（理）C　由题图知= 0的x值有4个，再由极值定义判断可知C为答案

　 （文）C　= 3x² – a．切线斜率：k = 3× 2² – a = 12 – a，又切线与x + 9y – 1 = 0垂直

　　　 则k = 9，∴12 – a = 9，即a = 3．

12．C　f (x) =，f (x₁ + x₂) = 1 –　　　　　 ①

　　　 又

　　　 令

　　　 ≥9代入①，得C项正确．

二、填空题

13．（理）950

　　　 提示：T_{r + 1} =

　　　 令3n – 5r = 0，得

　　　 再令r = 3k，k∈N^*，∴n = 5k < 100

∴1≤k≤19，k∈N^*

∴所有满足条件的n值的和是5 + 10 + 15 + … + 95 =× 19 = 950．

　 （文）7

14．

　　　 提示：由得到平移后直线方程2x – y + m = 0

　　　 而圆心（0，0）到2x – y + m = 0的距离d =

　　　 由垂径定理得m² = d² + ()²

　　　 即m² =+ 10，∴m =．

15．

提示：取A₁B₁，AB的中点D₁，D

　　　 由题意可知球心O是D₁D的中点且D₁D⊥AB

在Rt△ABC中，AB =

在Rt△AOD中，OD =，AD =

∴AO = 1，即球的半径为1

又∵在△AOC中，AC =，∴∠AOC =

∴AC两点间的球面距离为× 1 =．

16．99.6%

　　　 提示：即求目标函数z = 60x + 43y (z≤250cm)取最大值时的最优整数解问题．

　　　 当x = 2，y = 3时，z = 249

　　　 此时利用率 == 99.6%

三、解答题

17．解：f (x) = sin

　　　　　　　　 =

　 （1）T =．

　 （2）当x = k–(k∈Z)时，f (x)取最小值– 2．

　 （3）（理）令= 1

　　　 且得x =，即f ^{– 1}(1) =．

　 （文）由2k≤2x +≤2k

　　　 得k≤x≤k

　　　 ∴f (x)的单调递增区间为．

18．（理）解：（1）可能取的值为0，1，2，

　　　 P(= k) =，k = 0，1，2

　　　 所以的分布列为

	0	1	2
P

　 （2）由（1）得的数学期望为

　　　 E= 0 ×+ 1×+ 2 ×=

　 （3）由（1）知“所选3人中男生人数≤1”的概率为

　　　 P (≤1) = P (= 0) + P (= 1) =+=．

　 （文）解：（1）这名学生第一、二次射击未中目标，第三次击中目标的概率为

　　　 P₁ =

　 （2）这名学生恰好击中目标3次的概率为

　　　 P₂ =．

19．（1）解：由(p – 1)S_n = p² – a_n (n∈N^*)　　　　　　　　　 ①

　　　 由(p – 1)S_{n – 1} = p² – a_{n – 1}　　　　　　　　　　　　　　　　 ②

　　　 ① – ②得(n≥2)

　　　 ∵a_n > 0 (n∈N^*)

又(p – 1)S₁ = p² – a₁，∴a₁ = p

{a_n}是以p为首项，为公比的等比数列

a_n = p

b_n = 2log_pa_n = 2log_pp^{2 – n}

∴b_n = 4 – 2n

　 （2）（只理科做）证明：由（1）知，b_n = 4 – 2n，a_n = p^{2 – n}

　　　 又由条件p =得a_n = 2^{n – 2}

　　　 ∴T_n =　　　　　　　　　 ①

　　　　　　　　　　　②

① – ②得

= 4 – 2 ×

= 4 – 2 ×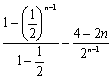

∴T_n =

T_n – T_{n – 1} =

当n > 2时，T_n – T_{n – 1}< 0

所以，当n > 2时，0 < T_n≤T₃ = 3

又T₁ = T₂ = 4，∴0 < T_n≤4．

　 （3）解：若要使a_n > 1恒成立，则需分p > 1和0 < p < 1两种情况讨论

　　　 当p > 1时，2 – n > 0，n < 2

　　　 当0 < p < 1时，2 – n < 0，n > 2

　　　 ∴当0 < p < 1时，存在M = 2

　　　 当n > M时，a_n > 1恒成立．

20．解法一：（1）取BC中点O，连结AO交BD于点E，连结PO

　　　 ∵PB = PC，∴PO⊥BC

　　　 又∵平面PBC⊥平面ABCD，平面PBC∩平面ABCD = BC

∴PO⊥平面ABCD

在直角梯形ABCD中

∵AB = BC = 2CD，易知Rt△ABO≌Rt△BCD

∴∠BEO =∠OAB +∠DBA =∠DBC +∠DBA = 90°

即AO⊥BD，由三垂线定理知PA⊥BD．

　 （2）连结PE，由PO⊥平面ABCD，AO⊥BD

得PE⊥BD

∴∠PEO为二面角P – BD – C的平面角

设AB = BC = PB = PC = 2CD = 2a

则PO =a，OE =

在Rt△PEO中，tan∠PEO =

∴二面角P – BD– C的大小为arctan

　 （3）取PB的中点为N，连结CN，则CN⊥PB

又∵AB⊥BC，BC是PB在面ABCD内的射影

∴AB⊥PB，又PB∩BC = B

∴AB⊥面PBC，∴平面PAB⊥平面PBC

∵CN⊥PB，面PAB∩面PBC = PB

∴CN⊥平面PAB

取PA的中点为M，连结DM、MN

则MN∥AB∥CD，∵MN =AB = CD

∴四边形MNCD为平行四边形

∴CN∥DM，∴DM⊥平面PAB

∴平面PAD⊥平面PAB．

解法二：（1）取BC中点为O

∵侧面PBC⊥底面ABCD，△PBC为等边三角形

∴PO⊥底面ABCD，以BC的中点O为坐标原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，直线OP为z轴，如图乙所示，建立空间直角坐标系．

不妨设CD = 1

则AB = BC = PB = PC = 2，PO =

∴A(1，– 2，0)，B (1，0，0)，D (– 1，– 1，0)，P (0，0，)

∴= (– 2，– 1，0)，= (1，– 2，–)

∵·= (– 2) × 1 + (– 1) × (– 2) + 0 × (–) = 0

∴⊥，∴PA⊥BD

　 （2）连结AO，设AO与BD相交于点E，连结PE

　　　 由· = 1 × (– 2) + (– 2) × (– 1) + 0 × 0 = 0

　　　 ∴⊥，∴OA⊥BD

又∵EO为PE在平面ABCD内的射影，∴PE⊥BD

∴∠PEO为二面角P – BD – C的平面角

在Rt△BEO中，OE = OB · sin∠OBE =

∴在Rt△PEO中，tan∠PEO =

∴二面角P – BD – C的大小为arctan

　 （3）取PA的中点M，连结DM

　　　 则M，又∵

　　　 ∴·=× 1 + 0 × (– 2) +

∴⊥，即DM⊥PA

又∵= (1，0，)

∴·=× 1 + 0 × 0 +

∴⊥，即DM⊥PB，∴DM⊥平面PAB

∴平面PAD⊥平面PAB．

21．解：（1）∵PF₁ + PF₂ = 2a > 2

∴点P的轨迹为椭圆，且半焦距c =

又∵与的夹角的最小值为arccos

∴∠F₁PF₂的最大值为arccos

又cos∠F₁PF₂ ==– 1

而PF₁ · PF₂≤

当且仅当PF₁ = PF₂时，取“=”号

∴cos∠F₁PF₂≥

∴a² = 5，则b² = 2

∴P点的轨迹方程为．

　 （2）∵点C (0，1)在椭圆

∴直线l与椭圆必有两个交点

　　　 ①当l的斜率不存在时，即l方程为x = 0

　　　 则A(0，)，B (0，–)

　　　 ，，

②当l的斜率为k时，直线l方程为y = kx + 1，代入

得(5k² + 2)x² + 10kx – 5 = 0

令A(x_­1，y₁)，B (x₂，y₂)，则x₁ · x₂ =

而= (x₁，y₁ – 1) · (x₂，y₂ – 1)

　　　　　　　= (x₁，kx₁) · (x₂，kx₂) = (1 + k²) x₁ · x₂

　　　　　　　==

∵5k² + 2≥2

∴–≤，∴

综合①，②得的取值范围为．

说明：本题是平面向量与解析几何的综合题，此类题型在高考中已多次出现．解题关键是把与夹角的最小值转化为∠F₁PF₂的最大值，然后利用基本不等式求出最值，从而解决问题．要注意向量夹角与三角形内角的区别，另外对直线斜率不存在时的讨论不能忘．

22．（理）解：（1）要使f ₁ (x)与f ₂ (x)有意义，则有

　　　

　　　 要使f ₁ (x)与f ₂ (x)在给定区间[a + 2，a + 3]上有意义，

等价于真数的最小值大于0

即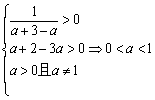

　 （2）f ₁ (x)与f ₂ (x)在给定区间[a + 2，a + 3]上是接近的

f ₁ (x) – f ₂ (x)≤1

≤1

log_a[(x – 3a)(x – a)]≤1

a≤(x – 2a)² – a²≤

对于任意x∈[a + 2，a + 3]恒成立

设h(x) = (x – 2a)² – a²，x∈[a + 2，a + 3]

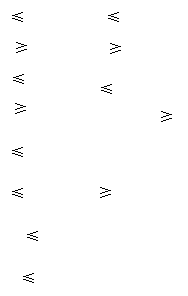且其对称轴x = 2a < 2在区间[a + 2，a + 3]的左边

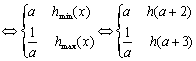
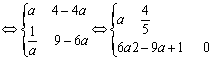
当时

f ₁ (x)与f ₂ (x)在给定区间[a + 2，a + 3]上是接近的

当< a < 1时，f ₁ (x)与f ₂ (x)在给定区间[a + 2，a + 3]上是非接近的．

　 （文）（1）证明：因f (m₁)，f (m₂)满足

　　　 a₂ + [f (m₁) + f (m₂)] a + f (m₁)f (m₂) = 0

　　　 即[a + f (m₁)] [a + f (m₂)] = 0

　　　 ∴f (m₁) = – a或f (m₂) = – a

∴m₁或m₂是f (x) = – a的一个实根

∴△≥0，即b²≥4a(a + c)

∵f (1) = 0，∴a + b + c = 0，a + c = – b

∴b²≥ – 4ab，∴b≥0时，b≥– 4a

又∵a > b > c，∴b < 0时，b≤– 4a舍去，∴b≥0．

　 （2）证明：设f (x) = ax² + bx + c = 0两根为x₁，x₂

　　　 则一个根为1，另一个根为

　　　 又∵a > 0，c < 0，∴

∵a > b > c且b = – a – c≥0

∴a > – a – c > c

∴– 2 <≤– 1，∴2≤x₁ – x₂ < 3．

　 （3）解：设f (x) = a (x – x₁)(x – x₂) = a (x – 1)

　　　 由已知f (m₁) = – a或f (m₂) = – a

　　　 不妨设f (m₁) = – a

　　　 则a (m₁ – 1) = – a < 0

　　　 ∴，∴m₁+ 3 >

∴f (m₁ + 3) > f (1) = 0，∴f (m₁ + 3) > 0

同理当f (m₂) = – a时，有f (m₂ + 3) > 0

∴f (m₂ + 3)或f (m₁ + 3)中至少有一个为正数．