2006年高考理科数学摸拟试题解析样本2

一. 选择题：( 本大题共12小题，每小题5分，共60分 )

1.已知集合P={(x，y)x+y=1}，Q={(x，y)x²+y²≤1}，则　　　　　  （A）

A.PQ　　　　　 B.P=Q　　　　　 C.PQ　　　　　 D.P∩Q=Q

　 答： 集合P表示正方形，集合Q表示圆面.

2.  的近似值（精确到小数后第三位）为　　　　　　　　　　　　  （A）

　  A.  726.089　　　　　　B.  724.089　　　　　　 　　　 C.　726.098　　　　　 　 D.　726.908

　 答：

3.　在中. 若 ，则 　　　　　　　　　　　　（C）

　　A. 　　　　　　　　 　　B.　　　　　　　 C.　　　　　　 D.　

 答：

4. 设为平面上以 为顶点的三角形区域( 包括边界 ),则　 的最大值和最小值分别为　　　　　　　　　　　　　　　 （A）

　  A.　14 , -18　　　　　  B.　-14 , -18　　　　 C.　18 , 14　　　　  D.　18 , -14

　答：画出示意图，易知：当动直线过时，取最大值；当动直线过时，取最小值.

5. 给定集合，定义 .若 ，则集合  中的所有元素之和为　　　　　　　　　　　　　  　 （A）

　  A.　15　　　　　　　  B.　14　　　　　　　 C. 　27　　　　　  D.　 -14

答A※B={3，2，1，4，5}，元素和为15．

6．　已知函数在上是减函数，则实数a的取值范围为（D）

　　　A. （5，+∞）　 　　B. （3，+∞）　　　 C. （-∞，3）　　　 D.

　　　 答　定义域为．而函数在时为增函数，故的单调减区间为，从而 ．

7．　设函数，若，则下列不等式必定成立的是（B）

　　　　　　　　　　　　　　　　　　　　A． 　　　　B． 　　　　　　　 C． 　　　　D．

　　　 答　易知，且当x∈时，为增函数．又由，得，故 ，于是．

8．　已知等比数列的首项为8，是其前n项的和，某同学经计算得S₂=20，S₃=36，S₄=65，后来该同学发现了其中一个数算错了，则该数为　　　　　　　 （C）

　　　 A． S₁　　　　　　　　　　B． S₂　　　　 　　 C． S₃　 　　　　　　　 D． S₄

　　　 　　　　　　　　　答　显然S₁是正确的．假设后三个数均未算错，则a₁=8，a₂=12，a₃=16，a₄=29，可知a₂²≠a₁a₃，故S₂、S₃中必有一个数算错了．若S₂算错了，则a₄=29=a₁q³，，显然S₃=36≠8(1+q+q²)，矛盾．只可能是S₃算错了，此时由a₂=12得，a₃=18，a₄=27，S₄=S₂+18+27=65，满足题设．

9．　函数的图象如图所示，则导函数的图象大致是（D）

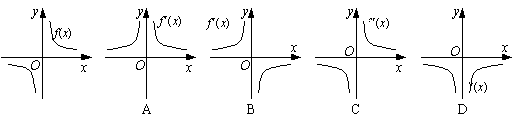
　　　 答　由的图象及的意义知，在x＞0时，为单调递增函数且＜0；在x＜0时，为单调递减函数且＜0．

10. 椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点、是它的焦点，长轴长为，焦距为，静放在点的小球（小球的半径不计），从点沿直线出发，经椭圆壁反弹后第一次回到点时，小球经过的路程是　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　  B．　　　　 C．　　D．以上答案均有可能

答⑴静放在点的小球（小球的半径不计）从点沿直线出发，经椭圆壁右顶点反弹后第一次回到点时，小球经过的路程是，则选B；

⑵静放在点的小球（小球的半径不计）从点沿直线出发，经椭圆壁左顶点反弹后第一次回到点时，小球经过的路程是，则选C；

⑶静放在点的小球（小球的半径不计）从点沿直线出发，经椭圆壁非左右顶点反弹后第一次回到点时，小球经过的路程是，则选A。

于是三种情况均有可能，故选D。

11. 用0，1，2，3四个数字组成没有重复数字的自然数，把这些自然数从小到大排成一数列，则1230是这个数列的　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A．第30项　　　　　　 B．第32项　　　　　　 C．第33项　　　　　　 D．第34项

答：用0，1，2，3四个数字组成没有重复数字的自然数,可分为4类：

⑴一位数，有4个（0也是自然数）；⑵两位数，有个；

⑶三位数，有个；　　⑷四位数，比1230小的有1023，1032。

于是，1230是这个数列的第34项。  选D．

12．半径为4的球面上有A、B、C、D四点，且满足，，，则的最大值为（为三角形的面积）　　　　　　　　　　　　　　　　　　　　　　　（C）

　　　 A．8　　　　　　　　　　　　B．16　　　　　　　　　　　C．32　　　　　　　　　　　D．64

答　易知AB，AC，AD两两互相垂直，进而AB²+AC²+AD²=(2r)²=64．

　　S_△ABC+S_△ACD+S_△ADB=≤=．

二、填空题：（本大题共4小题，每小题4分，共16分．）

13．已知双曲线(a＞0，b＞0)的半焦距为c，若b²-4ac＜0，则它的离心率的取值的范围是___________.

答.(1,2+) 化b²-4ac＜0＜为c²-a²-4ac＜0，从而变为＜，解关于的一元二次不等式，注意＞1.

14．对2×2数表定义平方运算如下：

　　　 ．　则　　．答  ．

15．为等差数列的前n项和，若，则=　　　　　　   ．

　　答　由，即 ，得．

　　，．故=4．

16．若，且，则的值是　　 11　　　．

答　由≥10，得　lg()≥lg10=1，即(lgx)²+(lgy)²≥1= (lgx+lgy)²，于是2lgxlgy≤0，从而lgx与lgy中必有一个为0，即x与y中必有一个为1，因而另一个为10．

三、解答题：（本大题共6小题，共74分．）

17．（本小题满分12分）已知 ，．

　　　（1）求的值；　　　　　　　　　　　　（2）求的值．

解　 （1）将已知两式平方相加得，故．………7分

　　　（2）∵，∴． ∴．……12分

18．（本小题满分12分）

对某种赌博游戏调查后，发现其规则如下：摊主在口袋中装入8枚黑和8枚白的围棋子，参加者从中随意一次摸出5枚，摸一次交手续费1元，而中彩情况如下：

摸子情况	5枚白	4枚白	3枚白	其它
彩金	20元	2元	纪念品价值5角	无奖同乐一次

　　现在我们试计算如下问题：

　 （1）求一次获得20元彩金的概率；（结果用最简分数表示）

　 （2）分别求一次获2元和纪念奖的概率；（结果用最简分数表示）

（3）如果有1000次摸奖，摊主赔钱还是挣钱？是多少元？（精确到元）

  解：（1）一次摸奖中20元彩金的概率，可见可能性很小……4分

　　（2）一次中2元彩金的概率　；……6分

　　而中纪念奖概率　　　　　……8分

　　（3）摊主赔钱还是挣钱由其支付完奖金余额决定，1000次收手续费1000元

　 预计支付20元奖需元；

支付2元奖需元；

　　支付纪念奖需

　　则余额　元

　　答：摊主应挣钱308元。　　　　　 …………12分

（3）另解：摸奖一次得到奖金ξ元，则随机变量ξ的分布列为：

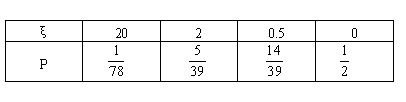
所以，

所以摊主挣钱，钱数为元。

19．（本小题满分12分）

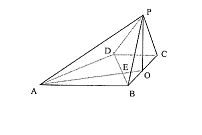
．　　如图，已知四棱锥P—ABCD的底面是直角梯形，，AB=BC=PB=PC=2CD=2，侧面底面ABCD，O是BC中点，AO交BD于E.

　　（I）求证：；

　　（II）求二面角的大小；

（III）求证：平面平面PAB.、

　

17．方法一：（I）证明：

　　又平面平面ABCD

　　平面平面ABCD＝BC，平面ABCD　　　　　　　　　……2分

　　在梯形ABCD中，可得

　　，即

　　在平面ABCD内的射影为AO，　　　　　　　　　　　　　　　　　　　　　　…4分

　　（II）解：，且平面平面ABCD

　　平面PBC　　 　　平面PBC，

　　为二面角P—DC—B的平面角　　　　　　　　　　　　　　　　　　　　　　 ……6分

　　是等边三角形即二面角P—DC—B的大小为 …8分

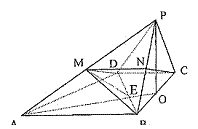
 （III）证明：取PB的中点N，连结CN

　　 ①

　　，且平面平面ABCD

　　平面PBC　　 ……10分

　　平面PAB　　平面平面PAB　②

　　 由①、②知平面PAB…………..10分

　　连结DM、MN，则由MN//AB//CD

　　，得四边形MNCD为平行四边形

　　　　　　　平面PAB　　　　　　　　　　　　　　

平面PAD　　平面平面PAB ……………….12分

方法二：

　　取BC的中点O，因为是等边三角形，

　　由侧面底面ABCD　　得底面ABCD ……1分

以BC中点O为原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，建立如图所示的空间直角坐标系O—xyz……2分

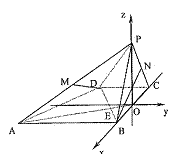
（I）证明：，则在直角梯形中，

　　在等边三角形PBC中，……3分

　　

　　　　　　　　　　　　　　　　　　　……4分

　　，即……6分

 （II）解：取PC中点N，则

　　

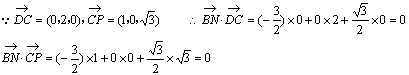
　　平面PDC，显然，且平面ABCD

　　所夹角等于所求二面角的平面角　　　　　　　　　　　　 ……8分

　　

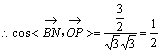
　　　　 二面角的大小为　　　　　 ……10分

（III）证明：取PA的中点M，连结DM，则M的坐标为

　　又　　　　　　　　　　　　　　　　　　……12分

　　　 

　　即

　　平面PAB，平面平面PAB　　　　　　　　　　　　　　　　　　　　　　　　……14分

20．（本小题满分12分）

　　　 是以为焦点的双曲线C：（a＞0，b＞0）上的一点，已知，．

　　　 （1）试求双曲线的离心率；

　　　 （2）过点P作直线分别与双曲线两渐近线相交于P₁、P₂两点，当，= 0，求双曲线的方程．

解　（1）∵，，　 ∴，．　

　　∵=0，∴(4a)²+(2a)²=(2c)²，∴．………………………………4分

　　（2）由（1）知，双曲线的方程可设为，渐近线方程为．…5分

　　设P₁(x₁，2x₁)，P₂(x₂，-2x₂)，P(x，y)．

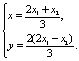　　∵，∴． ∵，∴………8分

　　∵点P在双曲线上，∴．

　　化简得，．∴．∴ ．　 ∴双曲线的方程为．……12分

21．（本小题满分12分）等比数列的首项为，公比．

（1）设表示该数列的前n项的积，求的表达式；

（2）当n取何值时，有最大值．

解　（1），．………………………………4分

（2）∵，

∴当n≤10时，＞1，∴ f(11) ＞ f(10) ＞…＞ f(1) ；6分

当n≥11时，＜1，∴ f(11) ＞ f(12) ＞…．………………8分

∵，∴的最大值为或中的最大者．10分

∵，

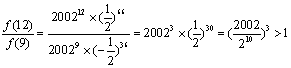∴ 当n=12时，有最大值为．………………………12分

22．（本小题满分14分）

　　　 设是定义在[-1，1]上的偶函数，的图象与的图象关于直线对称，且当x∈[ 2，3 ] 时， 2²²²3³．

　　　 （1）求的解析式；

　　　 （2）若在上为增函数，求的取值范围；

　　　 （3）是否存在正整数，使的图象的最高点落在直线上？若存在，求出的值；若不存在，请说明理由．

解：（1）当x∈[-1，0]时，2-x∈[2，3]，f(x)=g(2-x)= -2ax+4x³；当x∈时，f(x)=f(-x)=2ax-4x³，

　　∴…………………………………………………4分

　　（2）由题设知，＞0对x∈恒成立，即2a-12x²＞0对x∈恒成立，于是，a＞6x²，从而a＞(6x²)_max=6．…………………………………………………8分

　　（3）因f(x)为偶函数，故只需研究函数f(x)=2ax-4x³在x∈的最大值．

　　　 令=2a-12x²=0，得．…………10分　　若∈，即0＜a≤6，则

　　　 ，

　　　 故此时不存在符合题意的；

　　　若＞1，即a＞6，则在上为增函数，于是．

　　　　　 令2a-4=12，故a=8．　　　综上，存在a = 8满足题设．……………………………14分