全国1卷理
1.函数![]() 的单调增区间为
的单调增区间为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.![]() 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设函数![]() 。若
。若![]() 是奇函数,则
是奇函数,则![]() __________。
__________。
4. ![]() 的三个内角为
的三个内角为![]() ,求当A为何值时,
,求当A为何值时,![]() 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。
全国1卷文
5.已知向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
全国2卷理
6.函数![]() 的最小正周期是
的最小正周期是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7. 若![]() 则
则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8. 已知![]() 的三个内角A、B、C成等差数列,且
的三个内角A、B、C成等差数列,且![]() 则边BC上的中线AD的长为_______。
则边BC上的中线AD的长为_______。
9.已知向量![]()
(I)若![]() 求
求![]()
(II)求![]() 的最大值。
的最大值。
全国2卷文
10.在![]() ,求
,求
(1)![]()
(2)若点![]()
安徽理
11.在![]() 中,
中,![]() ,M为BC的中点,则
,M为BC的中点,则![]() _______。(用
_______。(用![]() 表示)
表示)
12.已知![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求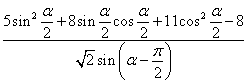 的值。
的值。
安徽文
13.对于函数![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
解:令![]() ,则函数
,则函数![]() 的值域为函数
的值域为函数![]() 的值域,而
的值域,而![]() 是一个减函减,故选B。
是一个减函减,故选B。
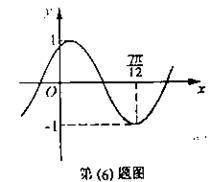 14.将函数
14.将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
解:将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象所对应的解析式为
平移,平移后的图象所对应的解析式为![]() ,由图象知,
,由图象知,![]() ,所以
,所以![]() ,因此选C。
,因此选C。
15.已知![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的值。
的值。
福建理
16.已知![]() ∈(
∈(![]() ,
,![]() ),sin
),sin![]() =
=![]() ,则tan(
,则tan(![]() )等于
)等于
A.![]() B.7
C.-
B.7
C.- ![]() D.-7
D.-7
17.已知函数f(x)=2sin![]() x(
x(![]() >0)在区间[
>0)在区间[![]() ,
,![]() ]上的最小值是-2,则
]上的最小值是-2,则![]() 的最小值等于
的最小值等于
A.![]() B.
B.![]() C.2
D.3
C.2
D.3
18.已知︱![]() ︱=1,︱
︱=1,︱![]() ︱=
︱=![]() ,
,![]() =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设![]() =m
=m![]() +n
+n![]() (m、n∈R),则
(m、n∈R),则![]() 等于
等于
A.![]() B.3
C.
B.3
C.![]() D.
D.![]()
19.已知函数f(x)=sin2x+![]() xcosx+2cos2x,x
xcosx+2cos2x,x![]() R.
R.
(I)求函数f(x)的最小正周期和单调增区间;
(Ⅱ)函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
 广东
广东
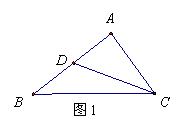
20.如图1所示,![]() 是
是![]() 的边
的边![]() 上的中点,则向量
上的中点,则向量![]()
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
21.已知函数![]() .
.
(I)求![]() 的最小正周期;
的最小正周期;
(II)求![]() 的的最大值和最小值;
的的最大值和最小值;
(III)若![]() ,求
,求![]() 的值.
的值.
湖北卷
22.已知向量![]() ,
,![]() 是不平行于
是不平行于![]() 轴的单位向量,且
轴的单位向量,且![]() ,则
,则![]()
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
23.若![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
24.设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)求函数![]() 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)将函数![]() 的图像按向量
的图像按向量![]() 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的![]() 。
。
湖南
25.已知![]() ,且关于
,且关于![]() 的方程
的方程![]() 有实根,则
有实根,则![]() 与
与![]() 的夹角的取值范围是 ( )
的夹角的取值范围是 ( )
A.[0,![]() ] B.
] B.![]() C.
C.![]() D.
D.![]()
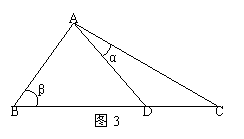 26.如图3,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=
26.如图3,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=![]() ,∠ABC=
,∠ABC=![]() .
.
(1)证明 ![]() ;
;
(2)若AC=![]() DC,求
DC,求![]() 的值.
的值.
27.已知向量![]() 若
若![]() 时,
时,![]() ∥
∥![]() ;
;![]() 时,
时,![]() ,则
,则
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
湖南文
28.设点P是函数![]() 的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值
的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值![]() ,则
,则![]() 的最小正周期是
的最小正周期是
A.2π
B. π C. ![]() D.
D. ![]()
29.若![]() 是偶函数,则a= .
是偶函数,则a= .
30.已知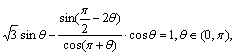 求θ的值.
求θ的值.
江苏
31.已知![]() ,函数
,函数![]() 为奇函数,则a=
为奇函数,则a=
(A)0 (B)1 (C)-1 (D)±1
32.为了得到函数![]() 的图像,只需把函数
的图像,只需把函数![]() 的图像上所有的点
的图像上所有的点
(A)向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
33.在△ABC中,已知BC=12,A=60°,B=45°,则AC= ▲
34.![]() = ▲
= ▲
山东
35.已知函数f(x)=A![]() (A>0,
(A>0,![]() >0,0<
>0,0<![]() <
<![]() 函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
函数,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求![]() ;
;
(2)计算f(1)+f(2)+… +f(2 008).
四川
36.已知A、B、C是⊿ABC三内角,向量![]() ,
,![]() ,且
,且![]() .
.
(I)求角![]() ;
;
(II)若![]() ,求
,求![]() .
.
浙江
37.函数y=![]() sin2+4sin
sin2+4sin![]() x,x
x,x![]() 的值域是
的值域是
(A)[-![]() ,
,![]() ]
(B)[-
]
(B)[-![]() ,
,![]() ]
]
(C)[![]() ]
(D)[
]
(D)[![]() ]
]
重庆
38.与向量a=![]()
![]() 的夹解相等,且模为1的向量是
的夹解相等,且模为1的向量是
(A) ![]() (B)
(B)
![]() 或
或![]()
(C)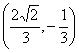 (D)
(D)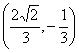 或
或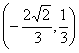
39.已知![]()
![]() ,sin(
,sin(![]() )=-
)=-![]() sin
sin![]() 则cos
则cos![]() =________.
=________.
40.已知三点![]() ,其中
,其中![]() 为常数。若
为常数。若![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为
(A)![]() (B)
(B)![]() 或
或![]()
(C)![]() (D)
(D)![]() 或
或![]()
41.已知![]() ,
,![]() ,则
,则![]() 。
。
42.设函数![]() (其中
(其中![]() )。且
)。且![]() 的图像在
的图像在![]() 轴右侧的第一个最高点的横坐标是
轴右侧的第一个最高点的横坐标是![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)如果![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值;
的值;