黄冈中学高考数学第三轮综合能力测试题(五)

一、选择题：

1．已知函数y＝f(x)　(x∈R)满足f(x＋3)＝f(x＋1)，且x∈[－1,1]时，f(x)＝x，则y＝f(x)与y＝log₅x的图象交点的个数是(　　)

　A．3　　　　　　　　　　　　B．4　　　　　　　　　　　　　　C．5　　　　　　　　　　　　D．6

2．已知△ABC中，若＝·＋·＋·，则△ABC是(　　)

　A．等边三角形　　　　B．锐角三角形　　　　　　C．直角三角形　　　　D．钝角三角形

3．已知定义在R上的函数f(x)的图象关于点(－,0)对称，且满足f(x)＝－f(x＋)，f(－1)＝1，f(0)＝－2，则f(1)＋f(2)＋…＋f(2005)的值为(　　)

　A．－2　　　　　　　　　　 B．－1　　　　　　　　　　　　C．0　　　　　　　　　　　　D．1

4．等差数列{a_n}的前n项和为S_n，且S₁＝1，点(n,s_n)在曲线C上，C和直线x－y＋1＝0交于A、B两点，且AB＝，则此数列的通项公式为(　　)

　A．a_n＝2n－1　　　　　 B．a_n＝3n－2　　　　　　　 C．a_n＝4n－3　　　　　 D．a_n＝5n－4

5．做一个面积为1m²，形状为直角三角形的铁架框，用下列四种长度的铁管，最合理(够用，且浪费最少)的是(　　)

　A．4.6m　　　　　　　　　 B．4.8m　　　　　　　　　　　C．5m　　　　　　　　　　 D．5.2m

6．已知集合A＝{1,2,3}，B＝{－1,0,1}，满足条件f(3)＝f(1)＋f(2)的映射f：A→B的个数是(　　)

　A．7　　　　　　　　　　　　B．6　　　　　　　　　　　　　　C．4　　　　　　　　　　　　D．2

7．若不等式4≤3sin²x－cos²x＋4cosx＋a²≤20对一切x都成立，则a的取值范围是(　　)

　A．[―5,―3]∪[3,5] B．[－4,4]　　　　　　　　　 C．[－3,3]　　　　　　　 D．[―4,―3]∪[3,4]

8．正三棱锥的侧棱长为m，底面边长为a，则的取值范围是(　　)

　A．[,＋∞)　　　　　 B．(,＋∞)　　　　　　　 C．[,＋∞)　　　　　 D．(,＋∞)

9．若复数Z＋i在映射f下的象为·i，则－1＋2i的原象为(　　)

　A．2　　　　　　　　　　　　B．2－i　　　　　　　　　　　　C．－2＋i　　　　　　　　D．－1＋3i

10．一同学投篮的命中率为，他连续投篮3次，其中恰有2次命中的概率为(　 )

　A．　　　　　　　　　　　　B．　　　　　　　　　　　　　C．　　　　　　　　　　　　D．

11．已知数列{a_n}对任意的n∈N^＋，满足a²_n＋2＝a_n·a_n＋4，且a₃＝2，a₇＝4，则a₁₅的值是(　　)

　A．8　　　　　　　　　　　　B．12　　　　　　　　　　　　　C．16　　　　　　　　　　　D．32

12．已知二项式(－x)⁶展开式中不含x的项为160，则tanθ值为(　　)

　A．2　　　　　　　　　　　　B．－2　　　　　　　　　　　　C．　　　　　　　　　　　　D．－

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：

13．定义非空集合A的真子集的真子集为A的“孙集”，则集合{1,3,5,7,9}的“孙集”的个数有＿＿＿＿＿个．

14．已知数列{a_n}满足a₁＝1，a_n＝a₁＋2a₂＋3a₃＋…＋(n―1)a_n―1(n≥2)．则其通项a_n＝＿＿＿＿＿＿＿＿

15．已知函数f(x)＝Log(x²―ax―a)的值域为R，且f(x)在(1＋,＋∞)上是减函数，则实数a的取值范围是＿＿＿＿＿

16．有两个向量＝(1,0)，＝(0,1)，今有动点P，从P₀(－1,2)开始沿着与向量＋相同的方向作匀速直线运动，速度为＋，另一动点Q，从Q₀(―2,―1)开始沿着与向量3＋2相同的方向作匀速直线运动，速度为3＋2，设P、Q在时刻t＝0时分别在P₀、Q₀处，则当⊥时，t＝＿＿＿＿＿＿秒．

三、解答题：

17．设函数f(x)＝4sinx·sin²(＋)＋cos2x，条件P：≤x≤；条件q：f(x)－m＜2，若p是q的充分条件，求实数m的取值范围．

18．甲、乙、丙三人分别独立解一道数学题,已知甲做对这道题的概率是，甲、丙两人都做错的概率是，乙、丙两人都做对的概率是．

(1)求乙、丙两人各自做对这道题的概率；

(2)求甲、乙、丙三人中至少有两人做对这道题的概率．

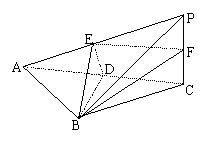19．已知三棱锥P－ABC中，PC⊥底面ABC，AB＝BC，D、F分别为AC、PC的中点，DE⊥AP于E．

(1)求证：AP⊥平面BDE．

(2)若AE∶EP＝1∶2，

求截面BEF分三棱锥

P－ABC所成的上、

下两部分的体积比．

20．已知f(x)在(－1,1)上有定义，f()＝－1，且满足x,y∈(－1,1)有f(x)＋f(y)＝f()，

(1) 判断f(x)在(－1,1)上的奇偶性；

(2)对数列x₁＝，x_n＋1＝，求f(x_n)．

(3)求证：＋＋…＋＞－．

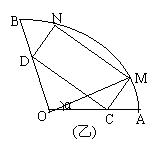
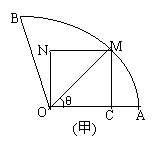
21．将一块圆心角为120°，半径为20cm的扇形铁片截成一块矩形，如图，有2种截法：让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行，请问哪种裁法能得到最大面积的矩形，并求出这个最大值．

22．已知双曲线c的中心在原点，抛物线y²＝8x的焦点是双曲线C的一个焦点，且双曲线c过点(,)．

(1)求双曲线C的方程；

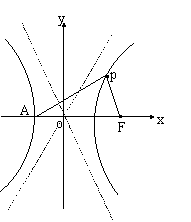
(2)设双曲线C的实轴左顶点为A，右焦点为F，在第一象限内任取双曲线C上一点P，试问是否存在常数λ(λ＞0)使得∠PFA＝λ∠PAF恒成立？并证明你的结论．

2006届高三数学第三轮复习训练题(五)参考答案

1．B　2．C

3．D　解：点(x，y)关于(－，0)对称点为(－－x，－y)，∴－y＝f(－－x)＝－f(－x)．

即f(－x)＝f(x)，f(x)偶，∴f(1)＝f(－1)＝1，又f(x)＝－f(x＋)＝f(x＋3)，∴T＝3，∴f(1)＋f(2)＋f(3)＋…＋f(2005)＝668·[f(1)＋f(2)＋f(3)]＋f(1)＝668·[1＋1－2]＋1＝1．

4．C　解：令y＝n²＋(1－)n＝n＋1n²－n－＝0，AB＝n₁－n₂＝·＝ ．∴d＝4，故a_n＝a₁＋(n－1)·d＝4n－3．

5．C　

6．A　解：f(3)＝f(1)＋f(2)

－1　　

0　　　　　共7个

1　　　　

7．D　解：4(cosx－)²≤a²≤4(cos－)²＋169≤a²≤16．

8．D　解：设侧面顶角为θ，则3θ＜360°，＜60°，sin＝＜＞．

9．A　解：·i＝－1＋2i＝i(2＋i)，∴z＝2－i，∴z＋i＝2．

10．D　解：P＝C·()²·(1－)＝．

11．C　解：∴q⁴＝＝2，∴a₁₅＝a₇·q⁸＝4×2²＝16．

12．B

13．26　解：φ，单元数集5个．2元素集＝10个，3元素集＝＝10个，共26个．

14．解：a_n＋1－a_n＝na_n∴＝n＋1(n≥2)．又a₁＝1，a₂＝1．

∴a_n＝a₁···…＝1·1·3·4·5…n＝(n≥2)

15．(―∞,―4]∪[0,2]　

解：令g(x)＝x²―ax―a，则g(x)＝0有解_△≥0a≤－4或a≥0　

a∈(―∞,―4]∪[0,2]

且a≤2．

16．2　解：＝t(＋)＝(t,t)，∴P(t－1,t＋2)，＝t(3＋2)＝(3t,2t)，

∴Q(3t―2,2t―1)．

∴＝(―1,―3)．＝(2t―1,t―3)．当·＝0时，t＝2．

17．解：f(x)＝2sinx[1－cos(＋x)]＋cos2x

＝2sinx(1＋sinx)＋1－2sin²x＝2sinx＋1

x

∵P∶≤x≤，∴2≤f(x)≤3．

由Pq．∴m－2＜f(x)＜m＋2．

∴m∈(1,4)．

18．解：(1)记甲、乙、丙三人独立做对这道题的事件分别为A、B、C，

依题得：

故乙、丙两人各自做对这道题的概率分别为，．

(2)甲、乙、丙三人中恰好有两人做对这道题的概率为P(AB＋AC＋BC)

＝P(A)·P(B)·P()＋P(A)·P()·P(C)＋P()·P(B)·P(C)

＝××＋××＋××

＝＋＋＝．

甲、乙、丙都做对这道题的概率为

P(ABC)＝××＝．

故甲、乙、丙三人中至少有两人做对这道题的概率为．

19．(1)证明：∵PC⊥底面ABC．∴PC⊥BD．

由AB＝BC，D为AC中点．∴BD⊥AC．

∴BD⊥面PACBD⊥PA．

又DE⊥PA．∴PA⊥面BDE．

(2)解：设点E和点A到平面PBC的距离分别为h₁和h₂，

则h₁∶h₂＝EP∶AP＝2∶3

∴＝＝·＝．

20．解：(1)令x＝y＝0．得f(0)＝0．令y＝－x．f(x)＋f(－x)＝0．

∴f(x)奇；

(2)f(x₁)＝f()＝－1，f(x_n＋1)＝f()＝f()＝f(x_n)＋f(x_n)

＝2f(x_n)，∴f(x_n)是以－1为首项，2为公比的等比数列，

∴f(x_n)＝―2^n―1．

(3) ＋＋…＋＝－(1＋＋＋…＋)

＝－2＋＞－2．

又－＝―2―＜－2．

∴原不等式成立．

21．解：在甲中，连OM，设∠MOA＝θ，θ∈(0, )，则S_矩＝200sin2θ．

∴当θ＝时，S_甲矩max＝200cm²．

在乙中，连OM，设∠MOA＝α,α∈(0, )．∵∠DOC＝120°．∴∠DCO＝30°．∠OCM＝30°＋90°＝120°．

∴∠OMC＝180°―α―120°＝60°－α．

在△OMC中，＝＝

∴MC＝sinα．同理OC＝sin(60°－α)．

又在△OCD中，CD＝2·CE＝2·OC·sin60°＝·OC＝40sin(60°－α) ．

∴S_乙矩＝CD·MC＝sinα·sin(60°－α)

＝[cos(2α－60°)－]．

∴当α＝30°时，S_乙矩max＝＞200．

故乙方案裁法得到最大面积矩形，最大值为cm²．

22．解：(1)依题设双曲线C方程：－＝1(a＞0,b＞0)．将(,)代入得－＝1．①

又抛物线y²＝8x的焦点为(2,0)

∴C的一个焦点为(2,0)．故c²＝a²＋b²＝4．②

由①②解得：a²＝1，b²＝3，故所求双曲线C的方程为x²－＝1．

(2)假设存在适合题意的常数λ(λ＞0)此时F(2,0)，A(－1,0)．

①当PF⊥x轴时，可得P(2,3)，PF＝AF＝3．

△PFA为等腰rt△，∠PFA＝90°，∠PAF＝45°．

此时λ＝2．

②当PF⊥x轴时，设∠PFA＝2∠PAF恒成立．

设P(x₁,y₁)(x₁＞0,y₁＞0)，K_PA＝．K_PF＝，

tan2∠PAF＝

＝＝．

又－＝1．

＝3(－1)＝3(x₁＋1)(x₁－1)代入③得：

tan2∠PAF＝＝－　　③

又∵tan∠PFA＝－K_PF＝－．

即tan2∠PAF＝tan∠PFA．易知2∠PAF∈(0,π)，∠PFA(0,π)．

∴∠PFA＝2∠PAF恒成立．

综合①②知：存在常数λ＝2．满足题设要求．