江西省重点中学协作体2006届高考第一次联考
数学试卷(理科)
命题人: 九江一中 江民杰 审题人: 九江一中 段训明 2006. 2. 9
一、选择题(12×5分=60分)
1. 复数Z=![]() 的共轭复数是( )
的共轭复数是( )
A. ![]() -
-![]() i
B. -
i
B. -![]() +
+![]() i C.
i C. ![]() +
+![]() i D. -
i D. -![]() -
-![]() i
i
2. (4x![]() -2x-5)(1-
-2x-5)(1-![]() )
)![]() 的展开式中, 常数项为( )
的展开式中, 常数项为( )
A. 21 B. -5 C. -16 D. -21
3. 设集合A=[-![]() ,
, ![]() ], B=[-1, 1], f: x
], B=[-1, 1], f: x![]() sinx是从集合A到集合B的映射, 则在映射f作用下, 像
sinx是从集合A到集合B的映射, 则在映射f作用下, 像![]() 的原像有( )
的原像有( )
A. 1个 B. 2个 C. 3个 D. 4个
4. 在首项为81, 公差为-7的等差数列{a![]() }中, 值最接近零的项是( )
}中, 值最接近零的项是( )
A. 第11项 B. 第12项 C. 第13项 D. 第14项
5. 圆x![]() +y
+y![]() -4x-2y+c=0与y轴交于A、B两点, 圆心为P, 若
-4x-2y+c=0与y轴交于A、B两点, 圆心为P, 若![]() APB=90
APB=90![]() , 则c的值为( )
, 则c的值为( )
A. -8 B. 8 C. -3 D. 3
6. 已知f(x)=lg(a![]() -b
-b![]() ), 当a>1>b>0时, f(x)在(1, +
), 当a>1>b>0时, f(x)在(1, +![]() )的值恒大于零, 则a、b应满足的充要条件是( )
)的值恒大于零, 则a、b应满足的充要条件是( )
A. a-b≥1 B. a-b>1 C. a-b=1 D. 0<a-b<1
7. 设m、n是两条不重合的直线, ![]() 、
、![]() 是两个不重合的平面, 则下列四个命题:
是两个不重合的平面, 则下列四个命题:
(1) 若m![]() n, m
n, m![]()
![]() , n
, n![]()
![]() , , 则n∥
, , 则n∥![]() (2) 若m∥
(2) 若m∥![]() ,
, ![]()
![]()
![]() , 则m
, 则m![]()
![]()
(3) 若m![]()
![]() ,
, ![]()
![]()
![]() , 则m∥
, 则m∥![]() 和m
和m![]()
![]() (4) 若m
(4) 若m![]() n, m
n, m![]()
![]() , n
, n![]()
![]() , 则
, 则![]()
![]()
![]() . 其中正确的命题是( )
. 其中正确的命题是( )
A. 仅(1) B. (2), (3) C. (2), (4) D. (1), (3), (4)
8. 已知![]() (1+
(1+![]() )
)![]() =e(e为常数), 则
=e(e为常数), 则![]() (1+
(1+![]() )
)![]() 等于( )
等于( )
A. 1 B.
e C. ![]() D. e
D. e![]()
9. 函数f(x)=![]() , 若a>b>c>0, 则
, 若a>b>c>0, 则![]() ,
, ![]() ,
, ![]() 的大小关系是( )
的大小关系是( )
A. ![]() <
<![]() <
<![]() B.
B. ![]() >
>![]() >
>![]()
C. ![]() >
>![]() >
>![]() D.
D. ![]() >
>![]() >
>![]()
10. 已知非零向量![]() 、
、![]() 不共线, 令p=
不共线, 令p=![]() -
-![]() , g=
, g=![]() -t
-t![]() (t
(t![]() R且t
R且t![]() 1), 若(
1), 若(![]() -
-![]() )·
)·![]() =0, 则( )
=0, 则( )
A. p<g B. p=g C. p>g D. 不能确定
11. 曲线y=x![]() 过点(
过点(![]() , 0)的切线的方程是( )
, 0)的切线的方程是( )
A. y=0 B. 3x-y-2=0 C. y=0或3x-y-2=0 D. x=0和3x-y-2=0
12. 在100, 101, 102, …, 999这些数中, 各位数字按严格递增或严格递减顺序排列的数共有( )
A. 216个 B. 204个 C. 168个 D. 120个
二、填空题(4×4分=16分)
13. 已知实数x、y满足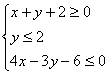 , 则集合A={(x, y) x
, 则集合A={(x, y) x![]() +y
+y![]() ≤r
≤r![]() , r>0}表示的图形面积的最大值是______________
, r>0}表示的图形面积的最大值是______________
14. 若不等式x-1<a![]() +a+1成立的充分条件是0<x<4, 则实数a的取值范围是______________
+a+1成立的充分条件是0<x<4, 则实数a的取值范围是______________
15. 数列{a![]() }中, 从第二项起每一项与前一项的差成等比数列, 则称该数列为差等比数列. 现已知a
}中, 从第二项起每一项与前一项的差成等比数列, 则称该数列为差等比数列. 现已知a![]() =1, 若差数列公比为1, 差数列首项为2, 则a
=1, 若差数列公比为1, 差数列首项为2, 则a![]() =_____________
=_____________
16. 设![]() =(cosx-sinx, 2sinx),
=(cosx-sinx, 2sinx), ![]() =(cosx+sinx, cosx), f(x)=
=(cosx+sinx, cosx), f(x)=![]() ·
·![]() , 给出下列四个命题:
, 给出下列四个命题:
(1) 函数在区间[![]() ,
,![]() ]上是减函数;
]上是减函数;
(2) 直线x=![]() 是函数图象的一条对称轴;
是函数图象的一条对称轴;
(3) 函数f(x)的图像可由函数y=![]() sin2x的图像按
sin2x的图像按![]() =(-
=(-![]() , 0)平移而得到;
, 0)平移而得到;
(4) y=f(x)的最小正周期是![]() .
.
其中正确的命题序号是_________________
三、解答题
17. (本小题12分)
△ABC中, AB=3, AC=4, ![]() BAC=60
BAC=60![]() .
.
(1) 求cos![]() ABC;
ABC;
(2) cos(![]() ABC+x)=-
ABC+x)=-![]() (-
(-![]() <x<0), 求cosx.
<x<0), 求cosx.
18. (本小题12分)
如图, A、B两点由5条连线并联, 它们在单位时间内能通过的最大信息量依次为2, 3, 4, 3, 2, 现记从中任取三条线且在单位时间内都通过的最大信息总量为![]() .
.
(1) 求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)  把
把![]() ≥10的并联网称为信息畅通, 把
≥10的并联网称为信息畅通, 把![]() =8或9的并联网称为信息基本畅通, 试分别求信息畅通、信息基本畅通的概率.
=8或9的并联网称为信息基本畅通, 试分别求信息畅通、信息基本畅通的概率.
19. (本小题12分)
如图, 已知多面体ABCDE中, AB![]() 平面ACD, DE
平面ACD, DE![]() 平面ACD, AC=AD=CD=DE=2a,
AB=a, F为CD的中点.
平面ACD, AC=AD=CD=DE=2a,
AB=a, F为CD的中点.
(1)  求证: AF
求证: AF![]() 平面CDE;
平面CDE;
(2) 求异面直线AC、BE所成角余弦值的大小;
(3) 求平面BCE和平面ACD所成锐二面角的大小.
20. (本小题12分)
设f(x)=ln(x+m), x![]() [2-m, +
[2-m, +![]()
![]() , x=
, x=![]() 是方程f(x)=x的一根.
是方程f(x)=x的一根.
(1) 求f(x)-2x的最大值;
(2) 定理: 设f(x)定义域为I, 对任意[a, b]![]() I, 存在x
I, 存在x![]()
![]() [a, b], 使等式f(b)-f(a)=(b-a) · f
[a, b], 使等式f(b)-f(a)=(b-a) · f![]() (x
(x![]() ). 求证: 方程f(x)=x有唯一解x=
). 求证: 方程f(x)=x有唯一解x=![]() .
.
21. (本小题12分)
已知F![]() (-1, 0), F
(-1, 0), F![]() (1, 0), 点P满足
(1, 0), 点P满足![]() +
+![]() =4
=4![]() .
.
(1) 写出点P的轨迹C![]() 的方程;
的方程;
(2) 曲线C![]() 上点M满足: MF
上点M满足: MF![]() =d+1, d表示M点到曲线C
=d+1, d表示M点到曲线C![]() 的左准线的距离, 过点F
的左准线的距离, 过点F![]() 的直线l 交曲线C
的直线l 交曲线C![]() 于A、B两点, 且△ABF
于A、B两点, 且△ABF![]() 被x轴分成的两个三角形面积比
被x轴分成的两个三角形面积比![]() =
=![]() (
(![]() ≤
≤![]() ≤3), 求直线l 的倾斜角的取值范围.
≤3), 求直线l 的倾斜角的取值范围.
22. (本小题14分)
正项数列{a![]() }满足a
}满足a![]() =1, n·a
=1, n·a![]() +(n-1) ·a
+(n-1) ·a![]() ·a
·a![]() -a
-a![]() =0(n≥2)
=0(n≥2)
(1) 求a![]() , a
, a![]() , a
, a![]() 及a
及a![]() ;
;
(2) 试确定一个正整数N, 使当n>N时,
不等式a![]() +a
+a![]() +2a
+2a![]() +3a
+3a![]() +…+(n-1) ·a
+…+(n-1) ·a![]() >
>![]() 成立;
成立;
(3) 求证: (1+![]() )
)![]() <1+a
<1+a![]() +a
+a![]() + … +a
+ … +a![]() .
.
参考答案
一、选择题(12×5分=60分) ADBCC ADCAA CB
二、填空题(4×4分=16分)
13. 2![]() ; 14. -2≤a≤-1或0≤a≤1; 15. a
; 14. -2≤a≤-1或0≤a≤1; 15. a![]() =2n+1(n
=2n+1(n![]() N*) 16. (1), (2)
N*) 16. (1), (2)
三、解答题(共6小题, 总分76分)
17. (1)BC=![]() =
=![]() …………2分 cosB=
…………2分 cosB=![]() =
=![]() >0
…………………5分
>0
…………………5分
(2) ∵cosB>0, ∴B为锐角, sinB=![]() ………7分
………7分
∵-![]() <B+x<
<B+x<![]() , cos(B+x)=-
, cos(B+x)=-![]() < 0
< 0
∴-![]() <B+x<
<B+x<![]() , ∴sin(B+x)=-
, ∴sin(B+x)=-![]() ………9分
………9分
∴cosx=cos[(B+x)-B]= … =-![]() ………12分
………12分
18. (1) P(![]() =7)=
=7)=![]() =
=![]() ,
P(
,
P(![]() =8)=
=8)= ![]() =
=![]() ,
,
P(![]() =9)=
=9)=![]() =
=![]() , P(
, P(![]() =10)=
=10)=![]() =
=![]() …………7分
…………7分
E![]() =8.4
…………8分
=8.4
…………8分
(2)
信息畅通的概率P![]() =P(
=P(![]() =10) =
=10) =![]() …………10分
…………10分
信息基本畅通的概率P![]() =P(
=P(![]() =8或
=8或![]() =9)=
=9)=![]() ………12分
………12分
19. (1) ∵DE![]() 平面ACD, ∴DE
平面ACD, ∴DE![]() AF
AF
又∵AC=AD=CD, F为CD的中点
∴AF![]() CD ∴AF
CD ∴AF![]() 平面CDE
………4分
平面CDE
………4分
(2) 取DE的中点G, 连AG、CG,
则![]() CAG或其补角就是异面直线AC、BE所成角
…………6分
CAG或其补角就是异面直线AC、BE所成角
…………6分
由题设可以求出: CG=AG =![]() a, AC=2a
a, AC=2a
∵cos![]() CAG=
CAG=![]() =
=![]()
∴异面直线AC、BE所成角的余弦值为![]() ………8分
………8分
(3) 延长DA、EB交于H点, 连CH, 则CH∥AF,
又由AF![]() 平面DCE, 故HC
平面DCE, 故HC![]() 平面DCE,
平面DCE,
从而![]() DCE就是平面BCE和平面ACD所成锐二面角
………10分
DCE就是平面BCE和平面ACD所成锐二面角
………10分
由平面几何知: △CDE为等腰直角三角形
∴![]() DCE=45
DCE=45![]()
∴平面BCE和平面ACD所成锐二面角为45![]() …………12分.
…………12分.
注: 采用向量法求解答题各小问的得分给出相应分数.
20. (1) 令g(x)=f(x)-2x=ln(x+m)-2x, 则g![]() (x)=
(x)=![]() -2
………2分
-2
………2分
∵x≥2-m ∴x+m≥2 ∴![]() ≤
≤![]()
从而g![]() (x)=
(x)=![]() -2≤
-2≤![]() -2<0
………4分
-2<0
………4分
∴g(x)在[2-m, +![]()
![]() 上单调递减
上单调递减
∴x=2-m时,
g(x)=f(x)-2x最大值=ln(2-m+m)-2(2-m)=ln2+2m-4 …………6分
(2) 假设f(x)=x还有另一解x=![]() (
(![]()
![]()
![]() ) 由假设知
) 由假设知
![]() -
-![]() =f(
=f(![]() )-f(
)-f(![]() )=f
)=f![]() (x
(x![]() )·(
)·(![]() -
-![]() ) x
) x![]()
![]() [2-m, +
[2-m, +![]()
![]() ……………8分
……………8分
故f![]() (x
(x![]() )=1, 又∵f
)=1, 又∵f![]() (x
(x![]() )=
)=![]() ≤
≤![]() <1 矛盾
…………11分
<1 矛盾
…………11分
故f(x)=x有唯一解x=![]() ………12分
………12分
21.
(1) P的轨迹椭圆C![]() :
: ![]() +
+![]() =1
……………4分
=1
……………4分
(2) 椭圆C![]() 的左准线方程为x=-8, F
的左准线方程为x=-8, F![]() (-1, 0),
(-1, 0),
由MF![]() =d+1知曲线C
=d+1知曲线C![]() 是以F
是以F![]() (-1, 0)为焦点, x=-9为准线的抛物线
(-1, 0)为焦点, x=-9为准线的抛物线
故C![]() 的方程为: y
的方程为: y![]() =16(x+5)
…………… 6分
=16(x+5)
…………… 6分
设l : x=ay-1, A(x![]() , y
, y![]() ), B(x
), B(x![]() , y
, y![]() ),
),
由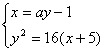 消去x得y
消去x得y![]() -16ay-64=0,
-16ay-64=0,
![]() =
=![]()
![]()
![]() =
=![]() 即
即![]() =
=![]()
![]() 于是:
于是:
y![]() =-
=-![]() y
y![]() ①
①
又y![]() +y
+y![]() =16a ②
=16a ②
y![]() ·y
·y![]() =-64 ③,
=-64 ③,
由①②③消去y![]() , y
, y![]() 得: a
得: a![]() =
=![]() (
(![]() +
+![]() -2), (
-2), (![]() ≤
≤![]() ≤3)
………9分
≤3)
………9分
当![]() ≤
≤![]() ≤1时, a
≤1时, a![]()
![]() [0,
[0, ![]() ],
],
当1≤![]() ≤3时, a
≤3时, a![]()
![]() [0,
[0, ![]() ],
],
∴a![]()
![]() [0,
[0, ![]() ]
……………10分
]
……………10分
从而当a=0时, 倾斜角为![]() ,
,
当a![]() 0时, k
0时, k![]() =
=![]() ≥3故k≥
≥3故k≥![]() 或k≤-
或k≤-![]() , 倾斜角
, 倾斜角![]()
![]() [
[![]() ,
, ![]()
![]()
![]() (
(![]() ,
, ![]()
![]() , 故倾斜角范围为: [
, 故倾斜角范围为: [![]() ,
,![]() ]
………………12分
]
………………12分
22. (1) n·a![]() +(n-1) ·a
+(n-1) ·a![]() ·a
·a![]() -a
-a![]() =0
=0![]() (n·
(n·![]() -1)(
-1)(![]() +1)=0,
+1)=0,
又∵a![]() >0, a
>0, a![]() >0, 故
>0, 故![]() =
=![]() , a
, a![]() =1
…………2分
=1
…………2分
a![]() =
=![]() =
=![]() , a
, a![]() =
=![]() , a
, a![]() =
=![]() , …, a
, …, a![]() =
=![]() ………4分
………4分
(2) 由(k-1)a![]() =
=![]() =
=![]() -
-![]() (k≥2),
(k≥2),
a![]() +a
+a![]() +2a
+2a![]() +3a
+3a![]() +…+(n-1) ·a
+…+(n-1) ·a![]()
=1+(![]() -
-![]() )+(
)+(![]() -
-![]() )+ … +(
)+ … +(![]() -
-![]() )=2-
)=2-![]() …… 6分
…… 6分
从而有2-![]() >
>![]() ,
,
∴![]() <
<![]() , 即n!>121,
, 即n!>121,
∵5!=120, 6!=720,
∴n>5取N=5, n>N时, 原不等式成立. …………8分
(3) (1+![]() )
)![]() 展开式通项:
展开式通项:
T![]() =C
=C![]() ·(
·(![]() )
)![]()
=![]() ·
·![]() ·
·![]() · … ·
· … ·![]() ·
·![]() <
<![]() (r=0, 1, 2, 3, …, n)…………12分 (1+
(r=0, 1, 2, 3, …, n)…………12分 (1+![]() )
)![]() <
<![]() +
+![]() +
+![]() +
+![]() + … +
+ … +![]() =1+a
=1+a![]() +a
+a![]() + … +a
+ … +a![]() ……14分
……14分