2006高考数学模拟试卷（3）

本试卷分第I卷（选择题）和第II卷（非选择题）两部分。满分150分。考试时间120分钟。

参考公式：

　　　 如果事件A、B互斥，那么

P（A＋B）＝P（A）＋P（B）

　　　 如果事件A、B相互独立，那么

P（A·B）＝P（A）·P（B）

　　　 如果事件A在一次试验中发生的概率是P，那么

n次独立重复试验中恰好发生k次的概率

P_n(k) ＝CP^k(1－P)^n－k

第Ⅰ卷  (选择题，共60分)

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知抛物线，则它的焦点坐标是

　　A．　　　 B．　　　　 C．　　　　  D．

2．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为y= -x²，值域为{-1，-9}的“同族函数”共有

　　　 A．8个　　　　　　　 B．9个　　　　　　　　　　C．10个　　　　　　　　　D．12个

3.下表是某班数学单元测试的成绩单：

学号	1	2	3	……	48	49	50
成绩	135	128	135	……	108	94	97

全部同学的学号组成集合A，其相应的数学分数组成集合B，集合A中的每个学号与其分数相对应．下列说法：①这种对应是从集合A到集合B的映射；②从集合A到集合B的对应是函数；③数学成绩按学号的顺序排列：135 ，128 ，135 ，…，108 ，94 ，97组成一个数列．以上说法正确的是　　　　　　　　　　　　　　　　　　　　

A． ①②　　　　　 B．①③　　　　　　 C．②③　　　　　 D．①②③

4．已知x＝a＋（a＞2），y＝()(b＜0) ，则x，y之间的大小关系是　　　 

A． x＞y　　　　  B ． x＜y　　　　　 C． x＝y　　　　 D．不能确定

5．已知A是三角形的内角，且sinA＋cosA=，则cos2A等于

　　 A．　　　　 B．－　　　　  C． 　　　 D．－

6．已知二面角的大小为，和是两条异面直线，则在下列四个条件中，能使和所成的角为的是　　　　　　　　　　　　　　　　　　　　　　　  

A． ∥，∥　　　　　　　　　 B． ∥，

C． 　　　　　　　　　　 D．  ，∥

7．已知函数反函数为，若，则最小值为　　　　　　　　　　　

A．　1　　　　B． 　　　 C． 　　　　D．

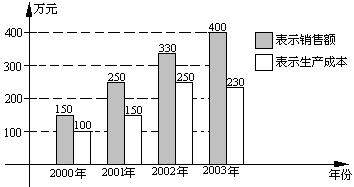
8. 下图是某企业2000年至2003年四年来关于生产销售的一张统计图表 (注: 利润＝销售额－生产成本). 对这四年有以下几种说法:(1) 该企业的利润逐年提高;

(2) 2000年—2001年该企业销售额增长率最快;

(3) 2001年—2002年该企业生产成本增长率最快;

(4) 2002年—2003年该企业利润增长幅度比2000年—2001年利润增长幅度大.

其中说法正确的是

A.(1)(2)(3)　B.(1)(3)(4)　C.(1)(2)(4)　D.(2)(3)(4)

9．在圆周上有10个等分点，以这些点为顶点，每三个点可以构成一个三角形，如果随机选择三个点，恰好构成直角三角形的概率是　　　　　　　　　　　　　　　　　 　

A．　　　　　　 B．　　 　 　　 C．　 　　　D．

10．抛物线上点A处的切线与直线的夹角为，则点A的坐标为

　 A．　(–1,1)　　　B．　　　 C． (1,1)　　　　 D． (–1,1)或

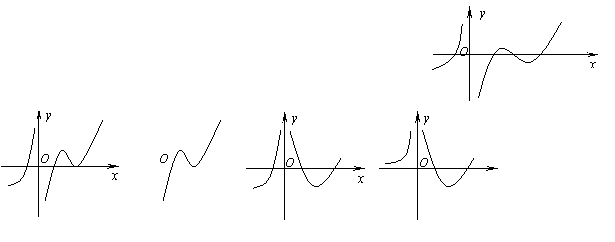11．设函数的图象如右图所示，则导函数的图像

可能为

					x

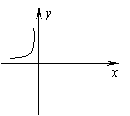A．　　　　　　  B．　　 　　　　 C．　　　　　　　　 D．

12．有限数列A＝(a₁，a₂，…，a_n)，为其前项和，定义为A的“凯森和”；如有2004项的数列(a₁，a₂，…，a₂₀₀₄)的“凯森和”为2005，则有2005项的数列(1，a₁，a₂，…，a₂₀₀₄)的“凯森和”为　　　　　　　　　　　　　　　　　　　　　 　　　　　　 （　　）

A．2004　　　　　　　　　 B．2005　　　　　　　　　 C．2006　　　　　　　　　 D．2008

第Ⅱ卷(非选择题，共90分)

二、填空题 ：本大题共4小题，每小题4分，共16分．

13．圆x²＋y²＝2上到直线x－y－4＝0距离最近的点的坐标是_________。

14．设三棱锥的三个侧面两两互相垂直，且侧棱长均为，则其外接球的体积为　　　。

15．点B是空间向量a=(2,1,2)在xoy平面上的射影,则=　　　。

16．已知命题p：m≥1，命题q：2m²－9m＋10＜0，若p，q中有且仅有一个为真命题，则实数m的取值范围是______________。

三、 解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.

17．(本小题满分12分)

在△ABC中， a、b、c分别是角A、B、C的对边，x＝（2a＋c，b）， y＝(cosB，cosC)，且x·y＝0 ，

（1） 求∠B的大小；

（2）若b＝，求a＋c的最大值。

18. (本小题满分12分)

某基本系统是由四个整流二极管（串，并）联结而成。已知每个二极管的可靠度为0.8（即正常工作的概率为0.8），若要求系统的可靠度大于0.85 ，请你设计出二极管的各种可能的联结方案（要求：画出相应的设计图形，并有相应的计算说明）。

19．(本小题满分12分)

如图，把正三角形ABC分成有限个全等的小正三角形，且在每个小三角形的顶点上都放置一个非零实数，使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等．设点A为第一行，…，BC为第n行，记点A上的数为a₁₁，…，第i行中第j个数为a_ij（1≤j≤i）．若a₁₁=1，a₂₁=，a₂₂=．

（Ⅰ）求a₃₁，a₃₂，a₃₃；

（Ⅱ）试归纳出第n行中第m个数a_nm的表达式（用含n，m的式子表示，不必证明）；

（Ⅲ）记S_n=a_n1+a_n2+…+a_nn，证明：n≤≤．

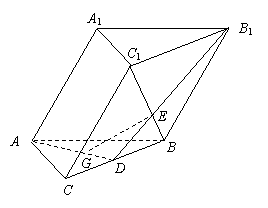20．(本小题满分12 分)

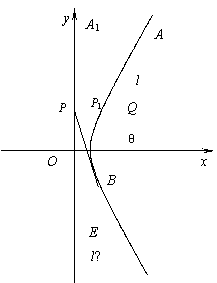
如图，在斜三棱柱中，底面是边长为2

的正三角形，G为它的中心，侧面A B BA⊥底面ABC，

侧棱AA₁=2，且与底面成的角，AG交BC于D点，

B₁D与BC₁交于E点．

（1）求证：GE∥侧面ABBA；

（2）求点E到侧面ABBA的距离；

（3）求二面角B₁－AD－B的大小．

21．(本小题满分12分)

已知f (x)＝x＋ax＋bx＋c在x＝1与x＝－时，都取得极值．

(1) 求a，b的值；

(2)若f (－1)=，求f (x)的单调区间和极值；

(3)若对x∈[－1，2]都有f (x)＜ 恒成立，求c的取值范围．

22．（本小题满分14分）

在直角坐标平面内，已知a＝（x＋2，y），b＝（x－2，y），且a－b＝2．

（1）求点M（x，y）的轨迹C的方程；

（2）过点D（2，0）作倾斜角为锐角的直线l与曲线C交于A、B两点，且→＝3→，求直线l的方程；

（3）是否存在过D的弦AB，使得AB中点Q在y轴上的射影P满足PA⊥PB？如果存在，求出AB的弦长；如果不存在，请说明理由．

参考答案及点评

一、选择题：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	B	D	A	B	C	B	D	B	D	D	B

1．  D

抛物线为x²=4y, 它的焦点坐标是(0,1),选(D)。

【点评】必须先把抛物线化为标准方程x²=4y,否则容易误选成(A)。

2．  B

定义域中可能有的元素为1，-1，3，-3，而且在1与 -1，3与 -3中各至少有一个在定义域内．当定义域中只有2个元素时，可有{1，3}，{1，-3}与{-1，3}，{-1，-3}，共4种可能；当定义域中含有3个元素时，可能=4种可能；当定义域中含有4个元素时，只有1种可能．由4+4+1=9．选（B）。

【点评】试题考查了分类讨论思想,分类时必须要”不重复,不遗漏”。

3．  D

对每一个学号的学生来说，这次考试都有唯一的分数。他们之间存在一一对应关系。故①②③全部正确，选（D）。

【点评】要正确解答本题，必须要准确理解映射、函数、数列的定义。

4．  A

x＝（a-2）＋ +2，y＝()<4。所以x<y。

【点评】本题考查了不等式的性质。将a转化为(a-2)+2是解题的关键。

5．  B

由sinA＋cosA=得,而A是三角形内角,因此。这样,选(B)。

【点评】注意三角形内角这一条件的运用。

6．  C

当时，两条异面直线和所成的角为，选（C）。

【点评】考查了线面垂直关系以及异面直线所成的角的意义。

7．  B

由条件知，a>0，b>0，且ab=16，所以 。

【点评】本题将反函数等知识与不等式进行了有机结合。

8．  D

根据图象,易得第(2)(3)(4)三种说法都是正确的,选（D）。

【点评】本题考查了学生的读图能力。

9．  B

根据等可能性事件的概率公式得， 。

【点评】本题事实上是通过概率问题考查排列组合知识。

10．D

（文）设，则过点的切线斜率为，由夹角公式即可求出= -1或．从而选（D）。

【点评】试题主要考查函数的切线以及直线的夹角公式。

11．D

根据y=f(x)图象的单调性，考察导数值的符号，选出答案为（D）。

【点评】本题考查了学生图形的识别能力，体现了多方面知识的交汇。

12．B

根据题中所给“凯森和”的定义，可得数列(1，a₁，a₂，…，a₂₀₀₄)的“凯森和”为2005，选（B）。

【点评】本题是“新定义”题型，是近年来高考数学的热点题型。

二、填空题：

 13．(1，－1)　　14． 36π　　 15．5　　　16．[1，2]∪[，＋∞）

13．(1，－1)

思路一：设动点的坐标为，利用点到直线距离公式，然后求最小值得，此时，从而点的坐标是（1，-1）；思路二：作圆x²＋y²＝2的与直线x－y－4＝0平行的直线，由图形位置，求出符合题意的切点即为（1，-1）。

【点评】解析几何中相关公式与方法必须要熟练掌握和运用。

14．36π

将三棱锥补成正方体，三棱锥的外接球即为正方体的外接球。由得R=3，因此三棱锥的外接球的体积为。

【点评】“割补法”是处理立体几何问题的重要的思想方法。

15．5

射影为点B(2,1,0), 则=5。

【点评】要了解点在平面上投影的概念。

16．[1，2]∪[，＋∞）

命题q等价于。分“p正确q错误”与“p错误q正确”两种情况讨论，易得结果为[1，2]∪[，＋∞）。

【点评】要准确把握“p，q中有且仅有一个为真命题”的含义。

三、解答题：

17．（1）x·y＝（2a＋c）cosB＋bcosC＝0，

由正弦定理　2sinAcosB＋sinCcosB＋sinBcosC＝0，　　

　　　　　  ∴2sinAcosB＋sin(B＋C)＝0　　 ∴sinA(2cosB＋1)＝0．

∵A，B∈(0，π)，∴sinA≠0，cosB＝－，∴B＝．　

（2）法一：3＝a²＋c²－2accos＝(a＋c)²－ac，　　　

　　　 (a＋c)²＝3＋ac≤3＋()²，　 ∴(a＋c)²≤4，a＋c≤2．

　　　∴当且仅当a＝c时，(a＋c)_max＝2．　　　　 

法二：2R＝＝＝2，A＋C＝．　　　　　

　　a＋c＝2(sinA＋sinC)＝2[sin(＋)＋sin(－)]　　

＝4sincos＝4×cos≤2．

当且仅当A＝C＝时，(a＋c)_max＝2．　　　　　

【点评】本题体现了向量与三角知识的交汇，小而巧。

18.⑴　全部并联，可靠度1-＝0.9984＞0.85

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

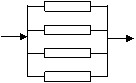
⑵　每两个串联后再并联，可靠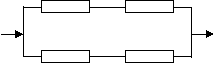度＝0.8704＞0.85

　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

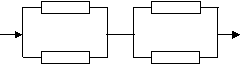
⑶　每两个并联后再串联，可靠度＝0.9216＞0.85

⑷　三个串联后再与第四个并联，可靠度1-0.2＝0.9024＞0.85

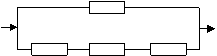
⑸　两个串联后再与第三、第四个并联，可靠度1-0.2²＝0.9856＞0.85

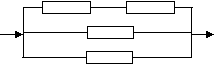
【点评】本题中将概率知识与物理学科综合设计，体现了多种知识的交汇。对五种可能的情形需要逐一讨论，较好地考查了学生分析问题和解决问题的能力。

19.解：（Ⅰ） ，∴．  ，∴．

 ，∴．∴，，．

（Ⅱ）由=1，a₂₁=，，……，

可归纳出，a₂₁，a₃₁，…，a_n1是公比为的等比数列， 故．

　　  由a₂₁=，a₂₂=，，，，

可归纳出，a_n2，a_n3，…，a_nn是公比为的等比数列，

故·，即．

（Ⅲ）由（Ⅱ）知，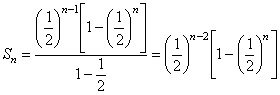

， ∴，

∴≥=．

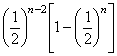又≤，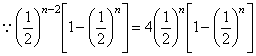

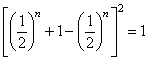∴1≤≤．∴n≤≤．

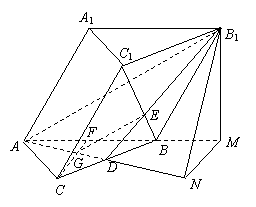【点评】本题中在平面图形背景下设计了一个数列问题,考查了数列的通项与求和等基本知识点,显得较有新意。

20．（1）∵G为正△ABC的中心，∴D为BC中点．

∴DE：EB₁＝BD：B₁C₁＝1：2＝DG：GA．

∴GE//AB₁．∵GEË面AA₁B₁B，AB₁Ì面AA₁B₁B，

∴GE//面AA₁B₁B．　　　　　　　　　

（2）由（1），E、G到平面AA₁B₁B等距离，

设CG交AB于F，则GF⊥AB．

∵面AA₁B₁B⊥面ABC，∴GF⊥面AA₁B₁B，GF＝AB＝．

∴E到面AA₁B₁B的距离为．

（3）作B₁M⊥AB于M，则B₁M⊥面ABC．

作MN⊥AD于N，连接B₁N，则B₁N⊥AD，所以∠B₁NM为二面角B₁－AD－B的平面角．

∵面AA₁B₁B⊥面ABC，∴∠B₁BM为侧棱与底面所成角，∠B₁BM＝60°．

B₁M＝B₁Bsin60°＝，BM＝B₁Bcos60°＝1，AM＝3，MN＝AMsin30°＝．

tan∠B₁NM＝＝＝，∴二面角B₁－AD－B为arctan．

【点评】本题通过一个常见问题的设计，研究了线与面和面与面之间的位置关系、数量关系。

21．（1）f ′(x)＝3x²＋2a x＋b＝0．

由题设，x＝1，x＝－为f ′(x)＝0的解．

－a＝1－，＝1×(－)．∴a＝－，b＝－2．

（2）f (x)＝x³－x²－2 x＋c，由f (－1)＝－1－＋2＋c＝，c＝1．

∴f (x)＝x³－x²－2 x＋1．

x	（－∞，－）	（－，1）	（1，＋∞）
f ′(x)	＋	－	＋

∴f (x)的递增区间为（－∞，－），及（1，＋∞），递减区间为（－，1）．

当x＝－时，f (x)有极大值，f (－)＝；当x＝1时，f (x)有极小值，f (1)＝－．

（3）由上，f ′(x)＝(x－1)(3x＋2)，f (x)＝x³－x²－2 x＋c，

f (x)在[－1，－)及（1，2］上递增，在（－，1）递减．

f (－)＝－－＋＋c＝c＋．f (2)＝8－2－4＋c＝c＋2．

由题设，c＋2＜恒成立，＜0，　∴c＜－3，或0＜c＜1 ．　　　

【点评】导数知识作为现行教材中的新增内容，在各类考试中均占有重要的地位。本题将导数与函数、不等式知识有机结合，是高考中的热点题型。

22．（1）∵a－b＝2，∴－＝2＜4．　

∴M(x，y)到点F（－2，0）和D（2，0）的距离差为2，

∴M点的轨迹是以F、D为焦点，实轴长为2的双曲线的右支，

∴a＝1，c＝2，b²＝3．

∴M点的轨迹方程是C：x²－＝1(x≥1)．　　　

（2）法一：设A（x₁，y₁），B（x₂，y₂），∵→＝3→，

∴（2－x₁，－y₁）＝3(x₂－2，y₂)，∴y₁＝－3 y₂，

设x＝my＋2，代入C：3(my＋2) ²－y²＝3，

(3m²－1)y²＋12my＋9＝0．

－2y₂＝y₁＋y₂＝，－3 y₂²＝y₁y₂＝．

∴()²＝，12m²＝1－3m²，m²＝．

由已知m＞0，l：x＝y＋2，即y＝( x－2)．　

法二：设A（x₁，y₁），B（x₂，y₂），

∵→＝3→，∴（2－x₁，－y₁）＝3(x₂－2，y₂)，∴x₁＋3 x₂＝8，y₁＝－3 y₂，

即

由①②④消去y₁ 、y₂得

x₁²－9x₂²＝－8，

　(x₁－3x₂)( x₁＋3x₂)＝－8，

将③代入得

　x₁－3x₂＝－1．　　⑤　　　　　　　　　 

由③⑤解得 x₁＝，

代入①得，y₁＝±．

∴k_l＝±（∵l的倾斜角为锐角，∴k_l＝－舍去），∴l：y＝( x－2)．

法三：设A、B在双曲线右准线l′上的射影为A₁，B₁，

AB交l′于E，l的倾斜角为θ（0＜θ＜）．

则DB,\d\fo1(→＝＝＝．∴EB＝AB＝×4BD，

EB＝2BD，又BD＝eBB₁，∴EB＝2eBB₁，∴e＝2．

∴cosθ＝＝，tanθ＝，∴l：y＝( x－2)．　

（3）法一：假设存在满足条件的弦AB，则PQ为Rt△PAB斜边上的中线，∴2PQ＝AB．

设Q（x₀，y₀），PQ＝x₀．

y₀＝＝，x₀＝my₀＋2＝＋2＝．

PQ＝＞0，m²＜．

(y₁－y₂)²＝()²－4×＝36×＝．

AB²＝(y₁－y₂)²＋(x₁－x₂)²＝(1＋m²) (y₁－y₂)²＝．

∴AB＝＝2PQ＝，∴m²＝－，不可能成立．∴不存在满足条件的弦．

法二：设PQ交双曲线的右准线l′于P₁，P₁Q为梯形AA₁B₁B中位线，

2PQ＝AA₁＋BB₁＝AD＋BD＝AB．∴AB＝4PQ．

假设存在满足条件的弦AB，则PQ为Rt△PAB斜边上的中线，

∴PQ＝AB＝2P₁Q，∴＋P₁Q＝2P₁Q，P₁Q＝，

又P₁Q≥2－＝，矛盾，∴不存在满足条件的弦．　

【点评】本题将向量与解析几何有机结合，考查了学生综合运用数学知识解决问题的能力。