2006年高考模拟测试数学3
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3页至8页,共150分。考试时间120分钟。
第Ⅰ卷(选择题共60分)
一、选择题:(每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.函数![]() 的最小正周期为 ( )
的最小正周期为 ( )
A.2π B.π C.![]() D.
D.![]()
2.如图,I是全集,M、N、S是I的子集,则图中阴影部分所示集合是 ( )
 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 的大致图象是
的大致图象是![]() ( )
( )
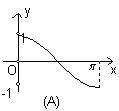



4.实数x,y满足x+2y=4,则3x+9y最小值为 ( )
A.18 B.12 C.![]() D.
D.![]()
5.若关于x的方程![]() 有解,则m的取值范围是( )
有解,则m的取值范围是( )
A.m>10 B.0<m<100 C.0<m<10 D.0<m≤10-3
6.某商场出售甲、乙两种不同价格的笔记本电脑,其中甲商品因供不应求,连续两次提价10%,
而乙商品由于外观过时而滞销,只得连续两次降价10%,最后甲、乙两种电脑均以9801元
售出.若商场同时售出甲、乙电脑各一台与价格不升不降比较,商场盈利情况是 ( )
A.前后相同 B.少赚598元 C.多赚980.1元 D.多赚490.05元
7.(理科做)在极坐标方程中,曲线C的方程是![]() ,过点
,过点![]() 作曲线C的切线,
作曲线C的切线,
则切线长为 ( )
A.4 B.![]() C.
C.![]() D.
D.![]()
(文科做)函数![]() 的最大值为( )
的最大值为( )
A.10 B.9 C.8 D.7
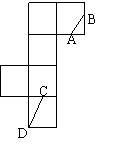 8.右图是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶
8.右图是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶
点,则在正方体中,异面直线AB和CD的夹角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.数列![]() 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且![]() 是等比数列
是等比数列![]() 的相
的相
邻三项.若b2=5, 则bn= ( )
A.5·![]() B.5·
B.5·![]() C.3·
C.3·![]() D.3·
D.3·![]()
10.过双曲线![]() 的右焦点F作一条长为
的右焦点F作一条长为![]() 的弦AB,将双曲线绕其右准线旋转
的弦AB,将双曲线绕其右准线旋转
240°,则由弦AB生成的曲面面积为 ( )
A.40π B.30π C.20π D.10π
11.设![]() 的展开式的各项系数之和为M,而二项式系数之和为N,且M-N=992.
的展开式的各项系数之和为M,而二项式系数之和为N,且M-N=992.
则展开式中x2项的系数为 ( )
A.250 B.-250 C.150 D.-150
12.某宇宙飞船的运行轨道是以地球的中心F为左焦点的椭圆,测得近地点A距离地面m
千米,远地点B距离地面n千米,地球的半径为k千米.关于椭圆有以下四种说法:
①焦距长为n-m;②短轴长为![]() ;③离心率为
;③离心率为![]() ;
;
④以AB方向为x轴的正方向,F为坐标原点,则左准线方程为![]()
以上正确的说法有 ( )
A.①③ B.②④ C.①③④ D.①②④
第Ⅱ卷(非选择题,共90分)
二、填空题:(每小题4分,共16分,把答案填在题中横线上。)
13.某区对口支援西部贫困山区教育,需从本区三所重点中学抽调5名教师,每所学校至
少抽调1人到山区5所学校支援,每校一人,则有 种支教方案.
14.数列![]() ,则数列的通项为an=
.
,则数列的通项为an=
.
15.过底面边长为1的正三棱锥的一条侧棱和高作截面,如果这个截面的面积为![]() ,那么
,那么
这个三棱锥的侧面与底面所成角的正切值为 .
16.一系列椭圆以定值线l为准线,所有椭圆的中心都在定点M,点M到l的距离为2,若
这一系列椭圆的离心率组成以![]() 为首项,公比为
为首项,公比为![]() 的等比数列,而椭圆相应的长轴长
的等比数列,而椭圆相应的长轴长
为Cn,则![]() 为
.
为
.
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(12分)已知关于x的方程:![]() 有实数根b.
有实数根b.
(1)求实数a,b的值;
(2)若复数z满足![]() 求,z为何值时,z有最小值,并求出z的值.
求,z为何值时,z有最小值,并求出z的值.
18.(12分)三棱柱ABC—A1B1C1的底面是边长为4的正三角形,侧面AA1C1C是菱形,
PA⊥BC,点P是A1C1的中点,∠C1CA=60°.
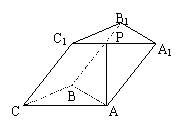 (1)求证:PA⊥平面ABC;
(1)求证:PA⊥平面ABC;
(2)求直线CC1与直线B1P所成角的正弦值;
(3)求四棱锥P—AA1B1B的体积.
19.(12分)函数![]() 对任意的m,n∈R都有
对任意的m,n∈R都有![]() ,并且当x>0
,并且当x>0
时,![]() .
.
(1)求证:![]() 在R上是增函数;
在R上是增函数;
(2)若![]() ,解不等式
,解不等式![]() .
.
20.(12分)(文科做)已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用
甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物
内至少含有56000单位维生素A和63000单位维生素B.
| 甲 | 乙 | 丙 | |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(1)用x,y表示混合食物成本c元;
(2)确定x,y,z的值,使成本最低.
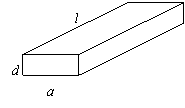
(理科做)一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度
d的平方成正比,与它的长度l的平方成反比.
(1)将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷变大吗?为什么?
(2)现有一根横断面为半圆(半圆的半径为R)的木材,用它来截取成长方形的枕木,
其长度即为枕木规定的长度,问如何截取,可使安全负荷最大?
 |
21.(12分)等比数列{an}首项为a1=2002,公比为![]() .
.
(1)设![]() 表示该数列的前n项的积,求
表示该数列的前n项的积,求![]() 的表达式;
的表达式;
(2)(理科做)当n取何值时,![]() 有最大值.
有最大值.
(文科做)当n取何值时,![]() 有最大值.
有最大值.
22.(14分)双曲线G的中心在原点O,并以抛物线![]() 的顶点为右焦点,以
的顶点为右焦点,以
此抛物线的准线为右准线.
(1)求双曲线G的方程;
(2)设直线![]() 与双曲线G相交于A、B两点,
与双曲线G相交于A、B两点,
①当k为何值时,原点O在以AB为直径的圆上?
②(理科做,文科不做)是否存在这样的实数k,使A、B两点关于直线![]() 为
为
常数)对称?若存在,求出k的值;若不存在,说明理由.
高考模拟测试3
数学答案及评分意见
一、选择题(每小题5分,共60分)
CABAD BC(D文)CDA BC
二、填空题:(每小题4分,共16分)
13.720 14.
![]() 15.2; 16.
15.2; 16.![]()
三、解答题:(共74分)
17.(12分)解
(1)∵b是方程![]() 的实根,∴(b2-6b+9)+(a-b)i=02分
的实根,∴(b2-6b+9)+(a-b)i=02分
故![]() …………………4分 解得a=b=3……………………6分
…………………4分 解得a=b=3……………………6分
(2)设![]() 由
由![]() ,得
,得![]() …8分
…8分
 即
即![]() ∴z点的轨迹是以O1(-1,1)为圆心,
∴z点的轨迹是以O1(-1,1)为圆心,
![]() 为半径的圆.……………………………10分
为半径的圆.……………………………10分
如图,当z点在OO1的连线上时,z有最大值或最小值,
![]() ,∴当z=1-i,时………………11分
,∴当z=1-i,时………………11分
最小值,![]() ……………………………12分
……………………………12分
18.(12分)证明:(1)∵四边形AA1C1C是菱形,∠C1CA=60°,∴△AC1A1是正三角形,又P是A1C1
的中点,∴PA⊥A1C1,……2分 ∴PA⊥AC. 又PA⊥BC,AC∩BC=C ∴PA⊥平面ABC.……4分
(2)由(1),PA⊥平面ABC,∴PA⊥平面 A1B1C1,由△AC1A1是正三角形,∴PB1⊥A1C1, 6分
∴B1P⊥平面AA1C1C,∴B1P⊥CC1. ∴CC1与B1P所成的角的正弦值为1.…………8分
(3)![]() ……10分
……10分 ![]() ……………12分
……………12分
19.(12分)(1)证明:设![]() ,且
,且![]() ,则
,则![]() ……………2分
……………2分
而![]() ………………4分
………………4分
![]() ∴
∴![]() 是增函数.……………………6分
是增函数.……………………6分
(2)解:![]()
![]() ……………8分
∴不等式即
……………8分
∴不等式即![]() ,
,
![]() 是增函数,∴
是增函数,∴![]() ……………10分 解得-3<a<2…………12分
……………10分 解得-3<a<2…………12分
20.(12分)解:(文科)解:(1)依题意,![]()
![]() 2分
2分
(2)由![]() 得,
得,![]() ,……4分
,……4分
![]() …………6分
…………6分 ![]() …………8分
…………8分
当且仅当![]() 时等号成立.……………10分 ∴当x=50千克,y=20千克,
时等号成立.……………10分 ∴当x=50千克,y=20千克,
z=30千克时,混合物成本最低为850元.………………………………………12分
(理科)解(1)安全负荷![]() 为正常数) 翻转
为正常数) 翻转![]() ………2分
………2分
![]() ,安全负荷变大.…4分当
,安全负荷变大.…4分当 ![]() ,安全负荷变小. 6分
,安全负荷变小. 6分
 (2)如图,设截取的宽为a,高为d,则
(2)如图,设截取的宽为a,高为d,则![]() .
.
∵枕木长度不变,∴u=ad2最大时,安全负荷最大.
![]() ……8分
……8分
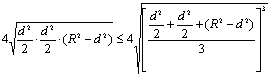
![]() .………………………………………10分,当且仅当
.………………………………………10分,当且仅当![]() ,即取
,即取![]() ,
,
取![]() 时,u最大, 即安全负荷最大.………………12分
时,u最大, 即安全负荷最大.………………12分
21.(12分)解:(1)等比数列的通项为![]() ……………………………2分
……………………………2分
前n项的积为![]() ………5分
………5分
(2)(文科)令![]() ,……6分
,……6分![]() ………………8分
………………8分
![]() ,…………………………………………10分
,…………………………………………10分
![]() ,b11是最大值.
,b11是最大值.
故当n=11时,![]() ……………………………12分
……………………………12分
(理科)![]() ………6分 ∴当
………6分 ∴当![]()
![]() >1,
>1,
![]() ……7分
当>10时,
……7分
当>10时,![]() <1,
<1,
![]() ,……………………………8分
,……………………………8分
![]()
![]() ……10分 故,只需比较f(9)与f(12)的
……10分 故,只需比较f(9)与f(12)的
大小就可以确定f(n)的最大值. ![]()
![]() ………………11分
………………11分
故,n=12时,f(n)有最大值![]() .…………………12分
.…………………12分
22.(14分)解:(1)抛物线![]() 的项点为
的项点为![]() (文2理1分)
(文2理1分)
准线为![]() ……………………………(文4,理2分)
……………………………(文4,理2分)
设双曲线G为![]() 则有
则有![]() ,可得,a2=3,b2=9.
,可得,a2=3,b2=9.
∴双曲线G的方程为![]() .……………………(文6,理4分)
.……………………(文6,理4分)
(2)①由![]() ,得
,得![]() ………………………………(文7分)
………………………………(文7分)
又由![]() .………(文8,理5分)
.………(文8,理5分)
设![]() …………………………(文9分)
…………………………(文9分)
∵若原点O在AB为直径的圆上,有OA⊥OB,KOA·KOB=-1,![]() ,即
,即
![]() ……(文10,理6分) 化简为
……(文10,理6分) 化简为![]()
![]() ………(文12,理7分)解得,
………(文12,理7分)解得,![]() .
.
![]() 故,当k=±1时,原点O在AB为直径的圆上.………(文14,理8分)
故,当k=±1时,原点O在AB为直径的圆上.………(文14,理8分)
②设这样的实数k存在,则有
|
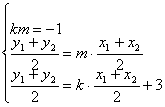
由②③得,![]() …………………………………………(12分)
…………………………………………(12分)
即![]() ,推得km=3,……………………………………(13分)
,推得km=3,……………………………………(13分)
这与km=-1矛盾,所以适合条件的k不存在.………………………(14分)