2006年高考模拟测试数学4
第Ⅰ卷(选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,
只有一项是符合要求的,请把正确答案的字母填在题后的括号内)
1.设集合A和集合B都是实数集R,映身f:A→B把集合A中的元素x映射到集合B中的
元素lg(x2+1),则在映射f下,象1的原象所成的集合是 ( )
A.{-1,1} B.{3,0} C.{3,-3} D.{3}
2.如果复数z适合z+2+2i=z,那么z-1+i的最小值是 ( )
A.4 B.![]() C.2 D.
C.2 D.![]()
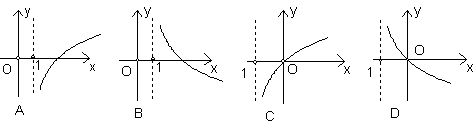 3.若函数
3.若函数![]() 为增函数,那么
为增函数,那么![]() 的图象是 ( )
的图象是 ( )
A. B. C. D.
4.![]() 展开式的各项系数和大于8且小于32,则展开式中系数最大的项是( )
展开式的各项系数和大于8且小于32,则展开式中系数最大的项是( )
A.6![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(理)直线![]() 关于直线
关于直线![]() 对称的直线的极坐标方程是 ( )
对称的直线的极坐标方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)把直线![]() 沿y轴正方向平移1个单位,再关于原点对称后,所得直线
沿y轴正方向平移1个单位,再关于原点对称后,所得直线
的方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设有如下三个命题:
甲:相交的直线l,m都在平面α内,并且都不在平面β内;
乙:直线l,m中至少有一条与平面β相交;丙:平面α与平面β相交 .
当甲成立时 ( )
A.乙是丙的充分而不必要条件; B.乙是丙的必要而不充分条件
C.乙是丙的充分且必要条件 D.乙既不是丙的充分条件又不是丙的必要条件.
7.△ABC的内角A满足![]() 则A的取值范围是 ( )
则A的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.直线![]() 、
、![]() 的倾斜角的取值范围是 ( )
的倾斜角的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在轴截面为直角三角形的圆锥内有一个内接圆柱,已知此圆柱的全面积等于该圆锥的侧
面积,则圆锥顶点到圆柱上底面的距离是圆锥母线长的 ( )
A.![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设Sn是等差数列{an}的前n项和,已知![]() ,则n等
,则n等
于 ( )
A.15 B.16 C.17 D.18
11.已知双曲线![]() ,给出以下四个命题:
,给出以下四个命题:
(1)双曲线C的渐近线方程是![]() ;
;
(2)直线![]() 与双曲线C只有一个交点;
与双曲线C只有一个交点;
(3)将双曲线![]() 向左平移1个单位,并向上平移2个单位可得到双曲线C;
向左平移1个单位,并向上平移2个单位可得到双曲线C;
(4)双曲线C的一个焦点到一条渐近线的距离为3.
其中所有正确命题的序号是 ( )
A.(1)(4) B.(2)(4) C.(2)(3) D.(3)(4)
12.若直线![]() 、
、![]() )始终平分圆
)始终平分圆![]() 的周长,则
的周长,则
a、b的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题)
二、填空题:(本大题共4小题,每小题4分,共16分。请把正确答案填在题中的横线上)
13.![]() .
.
14.从5名男生和4名女生中,选出3个分别承担三项不同的工作,要求3人中既有男生
又有女生,则不同的选配方法共 (用数字作答)种.
15.球面上有3个点,其中任意两点的球面距离都等于大圆周长的![]() ,经过这3个点的小
,经过这3个点的小
圆的周长为4π,那么这个球的半径为 .
16.椭圆![]() ,若离心率为e,则
,若离心率为e,则![]() 的最小值为
的最小值为
.
三、解答题:(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
17.(理)(本小题满分12分)若复数![]()
且![]()
![]() 的值.
的值.
(文)已知函数![]() (a为常数).
(a为常数).
(1)求反函数![]() 与它的定义域;
与它的定义域;
(2)如果![]() 上不同两点,求PQ中点R的坐标.
上不同两点,求PQ中点R的坐标.
18.(理)(本小题满分12分)如图所示:四棱锥P-ABCD底面一直角梯形,BA⊥AD,CD
 ⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点.
⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点.
(1)证明:EB∥平面PAD;
(2)若PA=AD,证明:BE⊥平面PDC;
(3)当PA=AD=DC时,求二面角E-BD-C的正切值.
(文)若复数![]()
且![]()
![]() 的值.
的值.
19.(理)(本小题满分12分)
已知数列{an}的前n项和![]()
(1)求数列{an}和{bn}的通项;
(2)求证存在自然数n0,对一切不小n0的自然数n,恒有an>5bn.
(文)如图所示:四棱锥P-ABCD底面一直角梯形,BA⊥AD,CD⊥AD,
CD=2AB,PA⊥底面ABCD,E为PC的中点.
 (1)证明:EB∥平面PAD;
(1)证明:EB∥平面PAD;
(2)若PA=AD,证明:BE⊥平面PDC;
(3)当PA=AD=DC时,求二面角E-BD-C的正切值.
20.(理)(本小题满分12分)某企业甲将经营状态良好的某种消费品专卖店以58万元的
优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息)。已知经营
该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)
 与售价p(元/件)的关系如图.
与售价p(元/件)的关系如图.
(1)写出销量q与售价p的函数关系式;
(2)当售价p定为多少时,月利润最多?
(3)企业乙最早可望在经营该专卖店几
个月后还清转让费?
(文) 已知数列{an}的前n项和
![]()
(1)求数列{an}和{bn}的通项;
(2)求证存在自然数n0,对一切不小n0的自然数n,恒有an>5bn.

21.(理)(本小题满分12分)如图:已知不垂直于x轴
的动直线l交抛物线![]() 于A、
于A、
B两点,若A、B两点满足![]()
原点O为PQ的中点.
(1)求证:A、P、B三点共线;
(2)当m=2时,是否存在垂直于x轴的直线l′,
使得l′被以AP为直径的圆所截得的弦长
为定值?如果存在,求出的l′方程;如果不存在,试说明理由.
(文)某企业甲将经营状态良好的某种消费品专卖店以58万元的
优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息)。已知经营
该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)
与售价p(元/件)的关系如图.
 (1)写出销量q与售价p的函数关系式;
(1)写出销量q与售价p的函数关系式;
(2)当售价p定为多少时,月利润最多?
(3)企业乙最早可望在经营该专卖店几个月后还清转
让费?
22.(本小题满分14分)
(理)已知函数![]()
是![]() 图象上不同的三点.
图象上不同的三点.
(1)如果存在正实数x,使![]() 、y2、y3成等差数列,试用x表示实数a;
、y2、y3成等差数列,试用x表示实数a;
(2)在(1)的条件下,如果实数x是唯一的,试求实数a的取值范围.
(文)如图:已知不垂直于x轴的动直线l交抛物线![]()
于A、B两点,若A、B两点满足![]() 原点O为PQ的中点。
原点O为PQ的中点。
(1)求证:A、P、B三点共线;
(2)当m=2时,是否存在垂直于x轴的直线l′,使得l′被以AP为直径的圆所
截得的弦长为定值?如果存在,求出的l′方程;如果不存在,试说明理由.

高考模拟测试4
数学参考答案及评分标准
一、选择题:(本大题共12小题,每小题5分,共60分)
1.C 2.D 3.C 4.A 5. C 6.C 7.C 8.B 9.C 10.D 11.B 12.A
二、填空题:(本大题共4小题,每小题4分,共16分)
13. ![]() 14.420 15.2
14.420 15.2![]() 16.
16.![]()
三、解答题:(本大题共6小题,共74分.)
17.(理)解:![]() .
. ![]() …2分
…2分
![]()
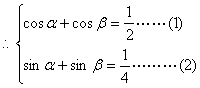 ………………………………………………………4分
………………………………………………………4分
(1)2+(2)2得:![]() ……………… ……6分
……………… ……6分
由(1)得:![]() …………(3)
…………(3)
由(2)得:![]() …………(4)……………………………8分
…………(4)……………………………8分
(4)÷(3)得:![]() …………………………………………………………10分
…………………………………………………………10分
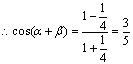 …………………………………………………………………12分
…………………………………………………………………12分
(文)解:(1)由![]() ……………2分
……………2分
![]() ……4分 定义域为
……4分 定义域为![]() …………………………5分
…………………………5分
(2)由已知得1=![]()
即![]() …9分
…9分
∴P(1,1)、Q(3,2).则PQ中点Q坐标是![]()
![]() …………………………12分
…………………………12分
18.(理)证明:(1)取PD中点Q,连EQ、AQ,则∵QE∥CD,CD∥AB,∴QE∥AB,
 又
又![]() ∥AQ
∥AQ
又![]() ∥平面PAD…3分
∥平面PAD…3分
(2)PA⊥底面ABCD ∴CD⊥PA,又CD⊥AD
∴CD⊥平面PAD ∴AQ⊥CD若PA=AD,
∴Q为PD中点,∴AQ⊥PD ∴AQ⊥平面PCD
∵BE∥AQ,∴BE⊥平面PCD…………………7分
(3)连结AC,取AC的中点G,连EG,EG∥PA,
∵PA⊥平面ABCD,∴EC⊥平面ABCD,过G作GH⊥BD,连EH,则EH⊥BD,
∴∠EHG是二面角E—BD—C的平面角.……………………………………………10分
设AB=1,则PA=AD=DC=2AB=2.
∴![]()
又![]()
![]() ∽△ABG,
∽△ABG,![]()
![]() ∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG.
∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG.
![]() .……12分
.……12分
(文)同(理)17题的答案.
19.(理)解:(1)![]() 时,
时,
![]()
![]() ……………………………………………………………………3分
……………………………………………………………………3分
又![]() …5分
…5分
![]() ………………………………………………7分
………………………………………………7分
(2)(i)当n=1时,![]() 不成立;
不成立;
(ii)当![]() 恒成立 即
恒成立 即![]() 恒成立
恒成立
只须![]() 恒成立……………………………………………………………11分
恒成立……………………………………………………………11分
由于![]() ………12分
………12分
(文)同(理)18题的答案.
20.(理)解:(1)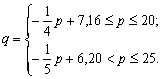 ………………………………………………3分
………………………………………………3分
(2)设月利润为W(万元),则W=(p-16)q-6.8
=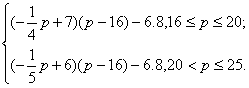 ……………………………………5分
……………………………………5分
当![]() ……7分
……7分
当![]()
∴当售价定为23元/件时,月利润最多为3万元…………………………9分
(3)设最早n个月后还清转让费,则![]()
∴企业乙最早可望20个月后还清转让费…………………………………12分
(文)同(理)19题的答案.
21.(理)解:(1)设![]() ……………………………………………1分
……………………………………………1分
∵∠AQP=∠BQP ∴tg∠AQP=tg∠BQP 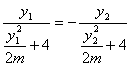 ……………3分
……………3分
![]()
![]() ……………………………………………………………………4分
……………………………………………………………………4分
∵O点是PQ的中点,且Q(-4,0),∴P(4,0)
又 …6分
…6分
![]() 、P、B三点共线………8分
、P、B三点共线………8分
(2)假设l′存在,设其方程为x=n. 设![]()
![]() 被圆截得的弦长为
被圆截得的弦长为
![]() …………………………………………10分
…………………………………………10分
=![]()
∴存在直线l′:x=3满足要求.……………………………………………………12分
(文)同(理)20题的答案.
22.(理)解:(1)f(x)的反函数是![]()
![]() P、Q、R是
P、Q、R是![]() 图象上不同三点,
图象上不同三点,![]() …2分
…2分
![]() 是不同三点,
是不同三点,![]() ……………………………………………………3分
……………………………………………………3分
已知y1、y2、y3成等差数列,即y1+y3=2y2
![]()
![]() ……①…………………………………………………5分
……①…………………………………………………5分
 (2)等量关系①等价于
(2)等量关系①等价于![]()
方程②等价于 ![]() ………………④
………………④
![]() ………………………………………………………8分
………………………………………………………8分
1°当![]() 方程④仅有一个实数解
方程④仅有一个实数解![]() 且满足③
且满足③
![]() 满足①有唯一解;
满足①有唯一解;
2°当![]() 方程②有二个相异实数解
方程②有二个相异实数解![]()
又![]() 满足条件③
满足条件③
![]() 是方程①的解………………………………………………………………………11分
是方程①的解………………………………………………………………………11分
要使方程①有唯一解,则x2不能是①的解 ![]()
![]()
![]() 的取值范围是
的取值范围是![]() ………………14分
………………14分
(文)同(理)21题的答案.
