2006年高考模拟测试数学5
第Ⅰ卷(选择题 共60分)
| |
(1)下列各式中,值为![]() 的是 ( )
的是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)已知![]() ,则
,则![]() 的大致图形是 ( )
的大致图形是 ( )


(3)如图,长方体ABCD—A1B1C1D1中,对角线AC1的长为![]() ,
,
![]() 则三棱锥C—B1C1D1的体
则三棱锥C—B1C1D1的体
积为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)已知等差数列{an},公差为2,且S100=10000,则a1+a3+a5+…+a99= ( )
(A)2500 (B)5050 (C)5000 (D)4950
(5)(理)如果θ是第二象限的角,那么直线![]() 的倾斜角的大小是
的倾斜角的大小是
( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(文)直线bx+ay=1(a<0,b<0=的倾斜角的余弦值是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)(理)已知三棱锥P—ABC的三个侧面与底面全等,且底面边长BC=2,AB=AC=![]() ,
,
则以BC为棱,以面BCP与面BCA为面的二面角的大小是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(文)已知三棱锥P—ABC的三个侧面与底面全等,且底面边长BC=2,AB=AC=![]() ,
,
则以BC为棱,以面BCP与面BCA为面的二面角的正弦值为 ( )
(A)![]() (B)1 (C)
(B)1 (C)![]() (D)
(D)![]()
(7)如果不等式![]() 成立的充分非必要条件是
成立的充分非必要条件是![]() ,则实数m的取值范围是
,则实数m的取值范围是
( )
(A)![]() (B)
(B)![]()
(C)![]() 或
或![]() (D)
(D)![]() 或
或![]()
(8)(理)已知函数![]()
![]() ,则
,则![]() 的值为 ( )
的值为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(文)若点P![]() 在直线
在直线![]() 上,则
上,则![]() 的值为 ( )
的值为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(9)![]() 展开式的第三项为10,则y关于x的函数图象的大致形状为 ( )
展开式的第三项为10,则y关于x的函数图象的大致形状为 ( )
 |
(10)(理)已知圆锥曲线的参数方程为 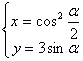 (α为参数),F1、F2为此曲线的两
(α为参数),F1、F2为此曲线的两
焦点,若以此曲线所在直角坐标系的原点为极点,x轴正半轴为极轴建立极坐标系,
则过F1、F2的直线的极坐标方程为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(文)已知曲线C与C′关于直线![]() 对称,若C的方程为
对称,若C的方程为![]() ,
,
则C′的方程为 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(11)设F1、F2是双曲线![]() 的两个焦点,P是双曲线上任意一点,从F1引∠F1PF2
的两个焦点,P是双曲线上任意一点,从F1引∠F1PF2
平分线的垂线,垂足为Q,则点Q的轨迹方程是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(12)有一位同学写了这样一个不等式:![]() ,他发现,当c=1,2,
,他发现,当c=1,2,
3时,不等式对一切实数x都成立,由此他作出如下猜测:
①当c为所有自然数时,不等式对一切实数x都成立;
②只存在有限个自然数c,对![]() 不等式都成立;
不等式都成立;
③当![]() 时,不等式对一切
时,不等式对一切![]() 都成立;
都成立;
④当![]() 时,不等式对一切
时,不等式对一切![]() 都成立.
都成立.
则正确的是 ( )
(A)①③ (B)② (C)①③④ (D)④
| |
(13)在等差数列{an}中,a3=0,S7=-14,已知等比数列{bn}中,b5=a5,b7=a7,则b6=
.
(14)若双曲线![]() 的一条准线是y轴,则m=
.
的一条准线是y轴,则m=
.
(15)若A=![]() ,从A中每次取出三个元素,使它们的和为3的倍数,
,从A中每次取出三个元素,使它们的和为3的倍数,
 则满足上述条件的不同取法的种数有 种.(用数字作答)
则满足上述条件的不同取法的种数有 种.(用数字作答)
(16)降水量是指水平地面上单位面积的降雨水的深度,
用上口直径为40cm,底面直径为28cm,深为
|
量,如果在一次降雨过程中,用此桶盛的雨水正
好是桶深的![]() ,则本次下雨的降水量是 (精确到1mm).
,则本次下雨的降水量是 (精确到1mm).
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
(理)解关于x的不等式:![]() ,(a>0且a≠1).
,(a>0且a≠1).
(文)解关于x的不等式:![]() ,(a>0且a≠1).
,(a>0且a≠1).
| |
(18)(本小题满分12分)
已知z1=3+4![]() ,z2=65
,z2=65![]()
![]() 且
且![]()
(Ⅰ)求![]() ;
;
(Ⅱ)设z1、z2在复平面内所对应点分别为P、Q、O为坐标原点,以OP、OQ为边作
平行四边形OPRQ,求对角线OR的长及平行四边形OPRQ的面积.
| |
(19)(本小题满分12分)
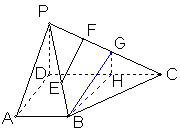
如图,已知四棱锥P—ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形, AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中
 点,F在PC上且PF=
点,F在PC上且PF=![]() PC.
PC.
(Ⅰ)求证EF//平面PAD;
(Ⅱ)求三棱锥E—PCD的体积.
| |
已知奇函数![]()
(Ⅰ)试确定实数a的值,并证明f(x)为R上的增函数;
(Ⅱ)记![]() 求
求![]() ;
;
(Ⅲ)若方程![]() 在(-∞,0)上有解,试证
在(-∞,0)上有解,试证![]() .
.
| |
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入Tn与时间n(以月为单位)的关系为Tn=an+b,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
| |
(22)(本小题满分14分,文科只做(Ⅰ)、(Ⅱ),理科全做)
已知抛物线C:![]() 的焦点为原点,C的准线与直线
的焦点为原点,C的准线与直线
![]() 的交点M在x轴上,
的交点M在x轴上,![]() 与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
(Ⅰ)求抛物线C的方程;
(Ⅱ)求实数p的取值范围;
(Ⅲ)若C的焦点和准线为椭圆Q的一个焦点和一条准线,试求Q的短轴的端点的轨迹方程.
高考模拟测试5
数学参考答案及评标准
一、 选择题(每小题5分,满分60分)本题考查基本知识和基本运算。
(理科)(1)B(2)C(3)C(4)D(5)A(6)B(7)A(8)A(9)A(10)A(11)C(12)A
(文科)(1)B(2)C(3)C(4)D(5)A(6)B(7)A(8)B(9)A(10)A(11)C(12)A
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分.
(13)![]() (14)m=12
(15)76 (16)32mm
(14)m=12
(15)76 (16)32mm
三、解答题
(17)本题考查函数性质、不等式等基础知识;考查运算能力和分类讨论思想. 满分12分.
(理)解:原不等式等价于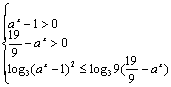 (5分)即
(5分)即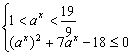 (6分)
(6分)
得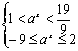 (7分)
(7分) ![]() (8分)
(8分)
当a>1时,不等式解集为![]() (10分)
(10分)
当0<a<1时,不等式解集为{![]() } (12分)
} (12分)
(文)解:![]() (6分)
(6分)
![]() (8分)
(8分)
当0<a<1时,a2<a,不等式解集为{![]() } (10分)
} (10分)
当a>1时,不等式解集为![]() (12分)
(12分)
(18)本题考查三角运算能力,考查复数的基本性质和基本运算,以及分析问题和解决问题的能力. 本题满分12分.
解:(Ⅰ)![]() (1分)
(1分)
![]() (2分)
(2分)
![]() (5分)
(5分)
![]() (6分)
(6分)
![]() (7分)
(7分)
(Ⅱ)![]() (9分)
(9分)
![]() (10分)
(10分)
又![]() (11分)
(11分)
![]() ∴S OPRQ =OP·OQ·sin(β-α)=253 (12分)
∴S OPRQ =OP·OQ·sin(β-α)=253 (12分)
(19)本题考查线面关系和棱锥体积计算,以及空间想象能力和逻辑推理能力,满分12分.
(I)证:∵侧面PAD⊥底面ABCD
CD⊥AD
 ∴CD⊥平面PAD
(2分)
∴CD⊥平面PAD
(2分)
同理AB⊥平面PAD且AB⊥AP
取DC、PC中点为H、G,连结BH、HG, 则BH⊥DC
又∠BCH=45°∴∠CBH=45°
由AB=AP=a,CH=HB=a,![]()
又CD=2a,
DP=a, ![]()
△ PBC中,G为PC中点,∴BG⊥PC
易得![]()
∴△BGH为直角三角形,且BG⊥GH ∴GB⊥平面PDC (5分)
∴GB⊥CD 又CD⊥HB ∴CD⊥平面BGH ∴平面BGH∥平面PAD
∴BG∥平面PAD ∵EF∥BG ∴EF∥平面PAD (7分)
(II)∵BG⊥平面PDC,EF∥BG ∴EF⊥平面PDC
∴EF为三棱锥E—PDC的高 (9分)
且EF=![]()
![]()
即![]() (12分)
(12分)
(20)本题考查函数概念、函数奇偶性、单调性、值域以及数列等基础知识;考查运算能力和逻辑思维能力. 满分12分.
解:(I)![]() 得
得![]()
![]() (2分)
(2分)
设![]()
![]()
![]()
![]()
![]() 在R上单调递增
(4分)
在R上单调递增
(4分)
(II)![]() (5分)
(5分)
![]()
![]() (7分)
(7分)
(III)![]()
又f(x)为奇函数,且在R上为单调增函数
![]() (9分)
(9分)
当![]()
欲使![]() 上有解
上有解
![]() (10分)
(10分)![]() 即
即![]()
即![]() (12分)
(12分)
(21)本题考查建立不等关系式、数列求和、解不等式等基础知识,考查综合运用数学知识解决实际问题的能力.满分12分.
解:入世改革后经过n个月的纯收入为![]() 万元
(3分)
万元
(3分)
不改革时的纯收入为![]() (6分)
(6分)
又![]() (7分)
(7分)
由题意建立不等式![]() (9分)
(9分)
即![]() (11分)
(11分)
![]()
答:经过13个月改革后的累计纯收入高于不改革时的累计纯收入. (12分)
(22)本题考查椭圆、抛物线的概念和性质,直线的性质;考查运算能力和逻辑思维能力,以及综合应用知识的能力.满分14分.
解:(I)由题意,抛物线顶点为(-n,0),又∵焦点为原点∴m>0
准线方程![]() 且有m=4n.
(2分)
且有m=4n.
(2分)
∵准线与直线![]() 交点在x轴上,交点为
交点在x轴上,交点为![]()
又![]() 与x轴交于(-2,0),∴m=4,n=1
与x轴交于(-2,0),∴m=4,n=1
∴抛物线方程为y2=4(x+1) (4分)
(II)由![]()
![]() ∴-1<k<1且k≠0
(5分)
∴-1<k<1且k≠0
(5分)
![]()
![]() (6分)
(6分)
∴AB的中垂线方程为![]()
得![]() (7分)
(7分)
∴p∈(2,+∞) (8分)
(III)∵抛物线焦点F(0,0),准线x=-2
∴x=-2是Q的左准线
设Q的中心为O′(x,0),则短轴端点为(±x,y) (9分)
(1) 若F为左焦点,则c=x>0,b=y
∴a2=b2+c2=x2+y2
依左准线方程有![]()
![]() 即y2=2x (x>0) (12分)
即y2=2x (x>0) (12分)
(2) 若F为右焦点,则x<0,故c=-x,b=y
∴a2=b2+c2=x2+y2 依左准线方程有![]()
即![]() 化简得2x2+2x+y2=0
化简得2x2+2x+y2=0
即![]() (x<0,y≠0) (14分)
(x<0,y≠0) (14分)
(理)难度系数参考
总体难度0.60与0.59之间
各题难度系数参考:
题号 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)
难度 0.96 0.92 0.89 0.95 0.92 0.85 0.8 0.8 0.85 0.83 0.45 0.45
题号 (13) (14) (15) (16) (17) (18) (19) (20) (21) (22)
难度 0.80 0.87 0.5 0.6 0.78 0.7 0.65 0.64 0.66 0.5
文科总体难度0.5
