2006年高考模拟测试数学7

第Ⅰ卷（选择题 共60分）

注意事项：

1．答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考场号、座号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试卷上。

3．考试结束，监考人将本试卷和答题卡一并收回。

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只一项是符合目要求的.

（1）已知全集I，M、N是I的非空子集，若，则必有　　　　　　　 （　　  ）

　　 （A）　（B）　（C）　　　 （D）

（2）在棱长为4的正方体ABCD—A₁B₁C₁D₁中，P是A₁B₁上一点，且，则多面体BC—PB₁C₁的体积为　 （　　 ）

　　 （A）　　　　　　（B）　　　　　

　　 （C）4　　　　　　 （D）16

（3）已知直线与平行，则实数a的取值是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　）

　　 （A）－1或2　　　 （B）0或1　　　　 （C）－1　　　　　　（D）2

（4）设、A为正常数，（　　　）

　　 （A）充要条件　　　　　　　　　　　　 （B）充分不必要条件

　　 （C）必要不充分条件　　　　　　　　　 （D）既不充分又不必要条件

（5）已知,则a、b、c的大小顺序

　　 是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　  ）

　　 （A）a>b>c　　　　 （B）c>a>b　　　　 （C）b>a>c　　　　　（D）b>c>a

（6）复数z满足条件则z的值为　　　　　　　　　（　　  ）

　　（A）　　　　　　　　　　　 （B）　　

　　（C）　　　　　　　　　　　 （D）

 （7）展开式的常数项是　　　　　　　　　　　　　　　　　（　　  ）

　　 （A）252　　　　　 （B）－252　　　　 （C）210　　　　　　（D）－210

 （8）已知下列命题：

　　 ①若直线a∥平面α，直线，则a∥b；

　　 ②若直线a∥平面α，平面β，，a在α内的射影为a′，则a′∥b；

　　 ③若直线a⊥直线c，直线b⊥直线c，则直线a∥直线b；

　　 ④若α、β、γ、δ是不同的平面，且满足∥

　　　δ，其中正确命题的序号是　　　　　　　　　　　　　　　　　　　　（　　  ）

　　 （A）①③　　　　　（B）②④　　　　　（C）②　　　　　　 （D）④

 （9）设△ABC的三边长a、b、c满足则△ABC是 （　　　）

　　 （A）钝角三角形　（B）锐角三角形　（C）等腰直角三角形 （D）非等腰的直角三角形

 （10）直线与椭圆交于A、B两点，O是坐标原点，当直线OA、

　　　OB的斜率之和为3时，直线AB的方程是　　　　　　　　　　　（　　 ）

　　 (A)2x－ey－4＝0　　(B)2x＋3y－4＝0　　(C)3x＋2y－4＝0　　 (D)3x－2y－4＝0

 （11）如图，△ABC是Rt△AB为斜边，三个顶点A、B、C在平面α内的射影分别是A₁、B₁、C₁.如果△A₁B₁C₁是等边三角形，且AA₁＝m，BB₁＝m＋2,CC₁＝m＋1,并设平面ABC与平面A₁B₁C₁所成的二面角的平面角为则的值为　　　　（　　  ）

　　 （A）　　　　　　（B）　　　　　（C）　　　　　 （D）

 （12）如图，半径为2的⊙○切直线MN于点P，射线PK从PN出发绕点P逆时针方向旋转到PM，旋转过程中，PK交⊙○于点Q，设∠POQ为x，弓形PmQ的面积为S＝f(x)，那么f(x)的图象大致是

第Ⅱ卷（非选择题 共60分）

二、填空题（本大题共4小题，每小题4分，共16分。把答案填在题中横线上）

 （13）设函数f(x)＝log_ax(a>0且a≠1)满足f(9)＝2，则f­^—1(log₉2)＝　　　　　　　　  .

　(14)点M在抛物线y²＝ax上运动，点N与点M关于点A（1，1）对称，则点N的轨迹方程是　　　　　　　　　　　　  .

　(15)有5列客车停在某车站并行的5条火车轨道上，若快车A不能停在第3道上，慢车B

　　　不能停在第1道上，则5列客车的停车方法共有　　　　　　　　种（用数字作答）.

 （16）已知数列{a_n}的通项a_n＝(2n＋1)·2^n—1,前n项和为S_n,则S_n＝　　　　　　　　　 .

三、解答题（本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤）

　 （17）（本小题满分10分）

　 已知0°<x<45°，且.

　 求cos

 (18)(本小题满分12分)

已知：在等差数列{a_n}中，a₁＝1，d≠0，若S_n＝a₁＋a₂＋……a_n, ＝a_n＋1＋a_n＋2＋……＋a_3n，且S_n与的比与n无关.

（Ⅰ）求等差数列{a_n}的通项公式；

（Ⅱ）求的值.

（19）（本小题满分12分）

如图，已知直三棱柱ABC—A₁B₁C₁中，AB＝AC，D为BC中点，F为BB₁上一点，

 BF＝BC＝2，FB₁＝1.

（Ⅰ）求证AD⊥平面BB₁C₁C；

（Ⅱ）若E为AD上不同于A、D的任一点，求证：EF⊥FC₁；

（Ⅲ）若A₁B₁＝3，求FC₁与平面AA₁B₁B所成角的大小.

 (20)(本小题满分12分)

某房地产公司要在荒地ABCDE（如图）上划出一块长方形地面（不改变方向）建造一幢8层楼公寓，问如何设计才能使公寓占地面积最大，并求出最大面积（精确到1m²）.

（21）（本小题满分14分）

如图，椭圆的中心在原点，长轴AA₁在x轴上.以A、A₁为焦点的双曲线交椭圆于C、D、D₁、C₁四点，且CD＝AA₁.椭圆的一条弦AC交双曲线于E，设，当时，求双曲线的离心率e的取值范围.

（22）（本小题满分14分

　已知二次函数设方程f(x)＝x有两个实数根x₁、x₂.

(Ⅰ)如果，设函数f(x)的对称轴为x＝x₀,求证x₀>—1;

(Ⅱ)如果，且f(x)＝x的两实根相差为2，求实数b 的取值范围.

高考模拟测试7

数学参考答案及评分意见

一、ABCADC　　BDBCCD　 二、（13）；（14）

三、（17）解：由已知等式可得

，……（4分）……（6分）

即，两边同加上1，得……（8分）

故……（10分）

（18）解（Ⅰ）设则……（2分）

即所以，…（4分）

由于（1）式与n无关，且d≠0，所以

解得……（6分）所以，等差数列的通项公式是（8分）

（Ⅱ）……（10分）

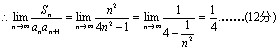
（19）解：如图，（Ⅰ）∵AB＝AC且D为BC的中点，∴AD⊥BC又∵ABC—A₁B₁C₁是直三棱柱，

∴平面ABC⊥平面BB₁C₁C. ∴AD⊥平面BB₁C₁C.……（4分）

（Ⅱ）连结DF，DC₁，由已知可求得即DF⊥CF₁，由三垂线定理∴EF⊥FC₁.……（8分）

（Ⅲ）作G₁G⊥平面AA₁B₁B，连结FG，∴C₁FG

为所求角.在Rt△ABD中，易求得

由于（12分）

（20）解：建立如原题图所示的坐标系，则AB的方程为由于点P在AB上，可设P点的坐标为……（2分）　则长方形面积……（6分）

化简得……（10分）易知，当（12分）

（21）解：设A（－c,0）,A₁(c,0)，则（其中c为双曲线的半焦距，h为C、D到x轴的距离）…（4分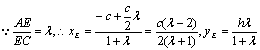）即E点坐标为……（6分）

设双曲线的方程为，将代入方程，得①

将代入①式，整理得……（10分）

消去……（12分）

由于……（14分）

（22）(Ⅰ)设

∴由条件……（2分）即（4分）

∴……（5分）对

……（8分）

（Ⅱ）由

……（11分）

由代入有……（14分）