高考模拟测试数学8

2014-5-11 0:13:23 下载本试卷

2006年高考模拟测试数学8

第Ⅰ卷（选择题 共60分）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有且只有一项是符合题目要求的.

1．若x>0，则由组成的集合中的元素有　　　（　　）

　　A．1个　　　　　　B．2个　　　　　　C．3个　　　　　D．7个

2．极坐标系中，圆的圆心坐标是　　　　　　　　　　　　　 （　　）

　　A．　　　　 B．　　　　 C．　　　D．

3．已知f（x）是定义在R上的奇函数，当x<0时，f(x)=那么的值是 （　　）

　　A．　　　　　 B．－　　　　 C．　　　　　D．－

4．若的值是　　　　　　　　　　　　　　　　　　 （　　）

　　A．　　　　　　　　　　　　　　　B．－　　　　

　　C．　　　　　　　　　　　　　　　D．－

5．在正方体ABCD—A1B1C1D1中，E是AD的中点，则异面直线

　 C1E与BC所成的角的余弦值是（　　）

　　A．　　　　　B．

　　C．　　　　　　 D．

6．若椭圆两焦点为点P在椭圆上，且△PF1F2的面积的最大值为12，则此椭圆的方程是　　　　　　　　　　　　　　　（　　）

　　A．　 B．　 C． D．

7．地球半径为R，北纬45。圈上A、B两点分别在东经130。和西经140。，并且北纬45。圈小圆的圆心为O，，则在四面体O—ABO，中，直角三角形有　　　　　　　　（　　）

　　A．0个　　　　　　B．2个　　　　　　C．3个　　　　　　　D．4个

8．设a，b是两个实数，给出下列条件：①a+b>1; ②a+b>2 ; ③a2+b2>2 ;④ab>1，其中能推出“a，b中至少有一个大于1”的条件是　　　　　　　　　　　　　　（　　）

　　A．①和④　　　　 B．②和④　　　　 C．②和③　　　　　 D．只有②

9．设矩形OABC的顶点O（坐标原点），A、B、C按逆时针方向排列，点A对应的复数为4－2i，且那么向量对应的复数是　　　　　　　　　　　　（　　）

　　A．3+4i　　　　　 B．－3+4i　　　　 C．－3－4i　　　　　D．3－4i

10．圆x2+y2－4x+2y+c=0与y轴交于A、B两点，圆心为P，若∠APB=90°，则c的值是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．－3　　　　　　B．3　　　　　　　C．　　　　 D．

11．某工厂8年来某种产品的总产量c与时间t（年）的函数关系如右图，下列四种说法：①前三年中产品增长的速度越来越快；②前三年中产品增长的速度越来越慢；③第三年后，这种产品停止生产；④第三年后，年产量保持不变，其中正确的说法是　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．②和③　　　　 B．①和④　　　　

　　C．①和③　　　　 D．②和④

12．一组实验数据如下：

t

y
 
　　

1.02

1.99

3.01

4.0

4.98

6.12

0.01

1.5

4.04

7.5

12

18.01

　　 则下列四个关系中，最接近实验数据的表达式（所谓最接近实验数据的表达式是指，将表中各组数据代入表达式后，等式左右两边值的差绝对值均不超过1）为　　　　　　　　　 （ 　 ）

　　A．　　 B．　　　　C．　　 D．

第Ⅱ卷　 (非选择题)

二、填空题：本大题有4小题，每小题4分，共16分.请将答案填写在题中的横线上.

13．直线l经过点A（2，1）和点B（1，m）（m∈R），那么直线l的倾斜角的取值范围是　

　　　 .

14．对于定义在R上的函数f（x），若实数x­0满足f（x0）­=x0，则称x0是函数f（x）的一个不动点.若二次函数f(x)=x2+ax+1没有不动点，则实数a的取值范围是　　　　  .

15．设正数数列{an}前n项和为S­n，且存在正数t，使得对所有自然数n，有，则通过归纳猜测可得到Sn=　　　　  .

16．某体育彩票规定：从01至36共36个号中抽出7个号为一注，每注2元.某人想从01至10中选3个连续的号，从11至20中选2个连续的号，从21至30中选1个号，从31至36中选1个号组成一注，这人把这种特殊要求的号买全，至少要化　　　 元.（用数学作答）

三、解答题：本大题有6小题，共74分.解答应写出文字说明，证明过程或演算步骤.

17．（本小题满分12分）

　　在△ABC中，已知且最长边为1.

（1）证明角；（2）求△ABC最短边的长.

18．（本小题满分12分）

　　　　已知四面体ABCD沿AB，AC，AD剪开展成的平面图形正好是下图所示的直角梯形

A1A2A3D（梯形中的三点A1，A2，A3重合于四面体中的点A）.

　 （1）证明：AB⊥CD；

　 （2）当A1D=10，A1A2=8时，求二面角A—CD—B的平面角；

　 （3）在（2）的条件下，求四面体ABCD的体积.

19．（本小题满分14分）

　　　　已知等差数列{an}的前四项和为60，第二项与第四项和为34；等比数列{bn}的前四项和为120，第二项与第四项和为90.

　 （1）求数列{an},{bn}的通项公式；

（2）是否存在正整数p.使得ap=b2 n对一切n∈N均成立？若存在请给出证明；若不存在，请说明理由.

20．（本小题满分12分）

　　已知函数

　 （1）当m=1时，解不等式

（2）如果对满足m<1的一切实数m，都有f（x）>g（x）求x的取值范围.

21．（本小题满分12分）

　　　　椭圆的中心在坐标原点O,右焦点F（c,0）到相应准线的距离为1，倾斜角为45°的直线交椭圆于A，B两点.设AB中点为M，直线AB与OM的夹角为a.

　 （1）用半焦距c表示椭圆的方程及tg;

　 （2）若2<tg<3，求椭圆率心率e的取值范围.

22．（本小题满分12分）

　　　　以一年为一个周期调查某商品出厂价格及该商品在商店销售价格时发现：该商品的出厂价格是在6元基础上按月份随正弦曲线波动的，已知3月份出厂价格最高为8元，7月份出厂价格最低为4元；而该商品在商店内的销售价格是在8元基础上按月份也是随正弦曲线波动的，并已知5月份销售价最高为10元，9月份销售价最低为6元.假设某商店每月购进这种商品m件，且当月能售完，请估计哪个月盈利最大？并说明理由.

高考模拟测试8

数学参考答案及标分标准

一、选择题：本大题共12小题，每小题5分，共60分.

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

B

B

D

A

C

C

C

D

B

A

A

C

二、填空题：本大题共4小题，每小题4分，共16分.

13．　　14.（－1，3）　　 15.n2t　　 16. 8640

三、解答题：本大题共6小题，共74分.

17．（本题满分12分）

（1）　　　 由而在△ABC中，0<A+B<π，所以

　（2）从而知∠C所对边最长，∠B所对边最短且为锐角，由tgB=;……3分　由正弦定理得最短边

18．（本题满分12分）

（1）依题意得，

（2）　　　 由条件可得，；那么在直角梯形A1A2CD中，求得CD=在△ACD中由余弦定理求得为二面角的平面角；因为

4分（3）4分

19．（本题满分14分）

（1）　　　 由等差等比数列的通项及求和公式，可求得a1=9,d=4,q=3……4分 所以通项为

（2）假设存在正整数P，使得ap=b2 n ，则4P+5=（3n）2,即4P=9n－5　……2分由归纳猜测可得对一切自然数，9n－5均是4的正整数倍，故存在正整数P，使得ap=b2 n .……2分

用数学归纳法或二项式定理证明以上结论.……4分

20．（本题满分12分）

（1）m=1时，不等式，等价于不等式组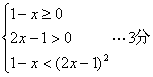

解得原不等式的解集为{}.……3分　（2）由f(x)>g(x)，即要对满足m<1的一切实数,不等式恒成立.……2分　令 必需且只需 解这两个不等式，等价于解，解得x的取值范围为

21．（本题满分12分）

（1）由题意可知所以椭圆方程为　设，将其代入椭圆方程相减，将代入 可化得 ……4分

（2）若2<tg<3，则…4分

22．（本题满分12分）

由条件可得：出厂价格函数为　销售价格函数为

则利润函数

…3分

所以，当x=6时，y=（2+）m，即6月份盈利最大.……3分