不等式·高考名题选萃

一、选择题

[　　]

A．R＜P＜Q　　　　　　　　　　　　　　　　　　　　　　　 B．P＜Q＜R

C．Q＜P＜R　　　　　　　　　　　　　　　　　　　　　　　 D．P＜R＜Q

2．设命题甲为：0＜x＜5；命题乙为：x－2＜3，那么……

[　　]

A．甲是乙的充分非必要条件

B．甲是乙的必要非充分条件

C．甲是乙的充分条件

D．甲不是乙的充分条件，也不是乙的必要条件

3．若log_a2＜log_b2＜0，则

[　　]

A．0＜a＜b＜1　　　　　　　　　　　　　　　　　　　　　　B．0＜b＜a＜1

C．a＞b＞1　　　　　　　　　　　　　　　　　　　　　　　　 D．b＞a＞1

4．若a、b是任意实数，且a＞b，则

[　　]

5．一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜，记三种盖法屋顶面积分别为P₁、P₂、P₃．

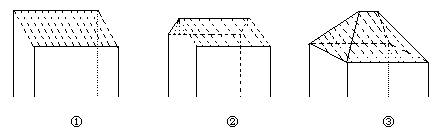
若屋顶斜面与水平面所成的角都是α，则

[　　]

A．P₃＞P₂＞P₁　　　　　　　　　　　　　　　　　　　　　　B．P₃＞P₂=P₁

C．P₃=P₂＞P₁　　　　　　　　　　　　　　　　　　　　　　　D．P₃=P₂=P₁

6．设集合M={x0≤x＜2}，集合N=xx²－2x－3＜0}，集合M∩N=

[　　]

A．{x0≤x＜1＝　　　　　　　　　　　　　　　　　　　　 B．{x0≤x＜2＝

C．{x0≤x≤1}　　　　　　　　　　　　　　　　　　　　　 D．{x0≤x≤2}

7．定义在区间(－∞，＋∞)上的奇函数f(x)为增函数；偶函数g(x)在区间[0，＋∞)上的图象与f(x)的图象重合．设a＞b＞0，给出下列不等式：

①f(b)－f(－a)＞g(a)－g(－b)；

②f(b)－f(－a)＜g(a)－g(－b)；

③f(a)－f(－b)＞g(b)－g(－a)；

④f(a)－f(－b)＜g(b)－g(－a)．

其中成立的是

[　　]

A．①与④　　　　　　　　　　　　　　　　　　　　　　　　　B．②与③

C．①与③　　　　　　　　　　　　　　　　　　　　　　　　　D．②与④

[　　]

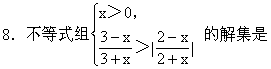
A．{x0＜x＜2＝　　　　　　　　　　　　　　　　　　　　 B．{x0＜x＜2.5}

9．若a＜b＜0，则下列结论中正确的是

[　　]

[　　]

11．某电脑用户计划用不超过500元的资金购买单价分别为60分、70元的单片软件和盒装磁盘．根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有

[　　]

A．5种　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．6种

C．7种　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．8种

二、填空题

13．建造一个容积为8m³，深为2m的长方体无盖水池，如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为________．

15．若正数a、b满足ab=a＋b＋3，则ab的取值范围是________．

三、解答题

(1)解不等式f(x)≤1；

(2)求a的取值范围，使函数f(x)在区间[0，＋∞)上是单调函数．

17．已知a＞0，a≠1，解不等式log_a(4＋3x－x²)－log_a(2x－1)＞log_a2．

20．已知关于x的实系数二次方程x²＋ax＋b=0有两个实数根α、β，证明：

①如果α＜2，β＜2，那么2α＜4＋b，且b＜4；

②如果2α＜4＋b，且b＜4，那么α＜2，β＜2．

22．已知a、b、c是实数，函数f(x)=ax²＋bx＋c，g(x)=ax＋b，当－1≤x≤1时，f(x)≤1．

(1)证明：c≤1；(2)证明：当－1≤x≤1时，g(x)≤2；

(3)设a＞0，当－1≤x≤1时，g(x)的最大值为2，求f(x)．

23．甲、乙两地相距s千米(km)，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时(km/h)．已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，比例系数为b；固定部分为a元．

(1)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；

(2)为了使全程运输成本最小，汽车应以多大速度行驶？

24．设二次函数f(x)=ax²＋bx＋c(a＞0)，方程f(x)－x=0的两个根，

(1)当x∈(0，x₁)时，证明x＜f(x)＜x₁；

25．如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A孔流入，经沉淀后从B孔流出，设箱体的长度为a米，高度为b米．已知流出的水中该杂质的质量分数与a、b的乘积ab成反比，现有制箱材料60平方米，问当a、b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小．(A、B孔的面积忽略不计)

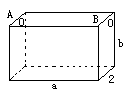
数a的取值范围．

　

参考答案提示

　

一、选择题

1．B　　　　　　　　　　　　 2．A　　　　　　 3．B　　　　　　　　 4．D

5．D　　　　　　　　　　　　 6．B　　　　　　 7．C　　　　　　　　 8．C

9．B　　　　　　　　　　　　 10．B　　　　　 11．C

提示：9．∵b＜0，∴－b＞0，∴a－b＞a．又∵a－b＜

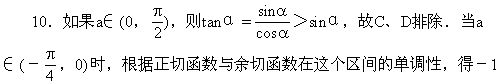
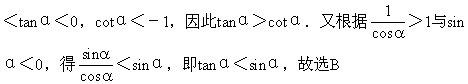
11．设购买了软件x片，磁盘y盒．根据题意，得不等式60x＋70y

y可取2，3，①有2组解．当x=5或6时，y只能取2，①均有1组解．综上，满足①的正整数解有7组，故选C

二、填空题

12．{x－2＜x＜1}　13．1760元　14．{x－2＜x＜4}

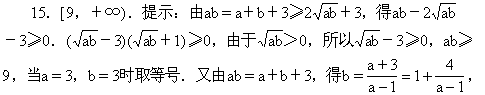
大时，ab的值也无限增大．所以ab的取值范围是[9，＋∞)

三、解答题

16．本小题主要考查不等式的解法、函数的单调性等基本知识，分类讨论的数学思想方法和运算、推理能力．

解  (1)不等式f(x)≤1即

由此得1≤1＋ax，即ax≥0，其中常数a＞0．

所以，原不等式等价于

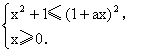
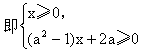
当a≥1时，所给不等式的解集为{xx≥0}．

(2)在区间[0，＋∞)上任取x₁，x₂，使得x₁＜x₂．

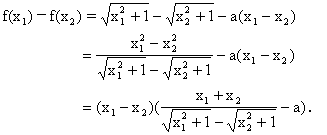
(Ⅰ)当a≥1时，

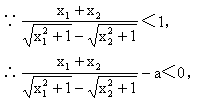
又x₁－x₂＜0，

∴f(x₁)－f(x₂)＞0，

即f(x₁)＞f(x₂)．

所以，当a≥1时，函数f(x)在区间[0，＋∞)上是单调递减函数．

满足f(x₁)=1，f(x₂)=1，即f(x₁)=f(x₂)，所以函数f(x)在区间[0，＋∞)上不是单调函数．

综上，当且仅当a≥1时，函数f(x)在区间[0，＋∞)上是单调函数．

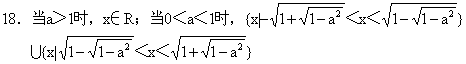
19．0＜x＜1或4＜x＜5

20．略

22．(3)f(x)=2x²－1

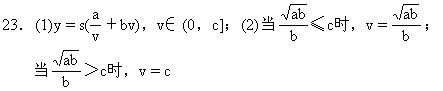
24．略

25．当a=6m，b=3m时，经沉淀后流出的水中该杂质的质量分数最小．

26．分析：本题考查绝对值不等式，分式不等式的解法，以及集合的知识．

解：由x－a＜2，得a－2＜x＜a＋2，

∴A={xa－2＜x＜a＋2}．

∴B={x－2＜x＜3＝．