茂名市2006年第二次高考模拟考试

  　　　 数　学　试　 卷

本试卷分第一部分（选择题）和第二部分（非选择题）两部分．第一部分1至2页，第二部分3至4页，满分分，考试时间分钟．

第一部分（选择题，共50分）

注意事项：

1.　　　　 答第一部分前，考生务必将自己的姓名、考生号、考试科目用铅笔涂写在答题卡上．

2.　　　　 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡

皮擦干净后，再选涂其它答案，不能答在试题卷上．

3.　　　　 考试结束，监考人员将本试卷和答题卡一并收回．

参考公式：

　　　 如果事件、互斥，那么　　　　　　　　　　　　　　　　　　　　　球的表面积公式

　　　 ，　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 如果事件、相互独立，那么　　　 　　　　　　　　　　　　　　其中表示球的半径

　　　 ，　　　　　　　　　　　　　　　　　　　　　　　 球的体积公式

　　　 如果事件在一次试验中发生的概率是，　　　　　　　　　　　　

　　　 那么在次独立重复试验中恰好发生次的概率　　　　　　　　　其中表示球的半径

　　　 ．

一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项

中，只有一项是符合题目要求的．

1、设A、B、C是三个集合，则“”是“B=C”的（　　 ）

  A　 充分但不必要条件　　　　　　　　  B　必要但不充分条件

  C　 充分且必要条件　　　　　  　　　　D　即不充分也不必要条件

2、已知向量，向量，且  =  ，则的坐标可以是

  A　（ｂ，－ａ）　 B　（－ａ，ｂ）　C　（ａ，－ｂ）　D　（－ｂ，－ａ）

3、设f (x)与g (x)是定义在R上的两个可导函数，若f (x)、g (x)满足，则f (x)与g (x)满足

  A　　f (x) = g (x)　　　　　　　　　　 B　　f (x) = g (x) = 0

C　　f (x) － g (x) 是常数函数　　　　　 D　　f (x) ＋g (x)是常数函数

4、已知，F₁( – 3,0) , Ｆ₂ (3 , 0)　满足 PF₁　–  PF₂  = 2m – 1　条件的动点P的轨迹是双曲线的一支。则m可以是下列数据： ① 2；　 ② – 1 ；　　③ 4 ；　　④ – 3 中的

  A　①②　　　 B　①③　　　  C　①②④　　　  D　②④　　　

5、若，则 a =　(　　)

A　1　　　　　　 B　2　　　　  C　 8　　　　　　 D　　10

6、如图所示，是已知函数的图象的

一段圆弧，若0 < x₁ < x₂ <2 ，则

  A　 < 　　　　B　　=

　C  > 　　　　 D 前三个判断都不正确

7、已知x 、 y 满足条件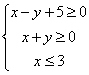，则 f (x , y ) = 2x + 4y的最小值是

　 A　5　　　　  B　– 6　　　　 C　10　　　 D　 – 10

8、若ABC的内角满足sinA + cosA > 0 ，tanA – sinA < 0 , 则角A的取值范围是

　 A　　　　 B　　　　 C　 　　　　D　

9、若( 1 +2x )( 1 + 4x )( 1 + 6x )…（1 +2006x ）的展开式中x的一次项系数为m，则=

　 A　 　　　　B　　　　　　 C　　– 1　　　　  　 D　 1

10、二面角的平面角为120⁰ ,在内AB于点B，AB =2 , 在内CD于点D，CD = 3 , 且BD = 1 ，若M为  上的一动点，则AM+ CM的最小值是

  A　 + 3　　　 B　　　　　C　2　　　　　 D　 2

第二部分（非选择题，共100分）

二．填空题：（本大题共4小题，每小题5分，共20分，把答案填在答题卷相应题目上）．

11、5人站成一排，甲、乙两人要在一起的不同站法的种数有___________种（用数字作答）

12、已知圆的半径为2，圆心在轴的正半轴上，且圆与直线3x + 4y +4 = 0相切，则圆的标准方程是_______________________

13、已知正方体ABCD – A₁B₁C₁D₁ 的棱长为2，在正方体表面上的与点A距离为1的点的集合形成一曲线（此曲线不一定在同一平面上），则此曲线的长度之和为___________ ；在此正方形内与点距离为1的点的集合形成一曲面，则此曲面的面积为_____________；（答案要保留值）

14、设，数列满足

 , 则数列的通项 =_______________

三．解答题：（本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤）．

15、（本小题满分12分）

　 已知函数 .

（1）求函数f (x) 图象的对称轴方程、对称中心坐标；并指出它的最大值、最小值；（8分）

（2）试说明函数f (x) 的图象可由 y = sinx 的图象经过怎样的变换而得到？（4分）

 

16、（本小题满分12分）

  已知函数，其中。

（！）求并判断函数 y =  的增减性；（4分）

（2）若命题P：为真命题，求实数 x 的取值范围。（8分）

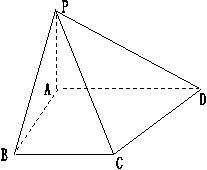17、（本小题满分14分）

　　　　如图，在四棱锥P – ABCD 中，底面ABCD是一

直角梯形，∠BAD= 90⁰ , AD∥BC , AB=BC=a ,

AD = 2a , 且PA⊥底面ABCD，PD与底面成30⁰的角。

（1）试在棱PD上找一点E，使PD⊥平面ABE；（7分）

（2）若点E满足（1），求异面直线AE与CD所成的角

的大小。

18、（本小题满分14分）

甲、乙两个商店购进同一种商品的价格为每件30元，销售价均为每件50元。根据前5年的有关资料统计，甲商店这种商品的需求量ξ服从以下分布：

ξ	10	20	30	40	50
P	0.15	0.20	0.25	0.30	0.10

乙商店这种商品的需求量服从二项分布~ B ( 40，0.8 )

若这种商品在一年内没有售完，则甲商店在一年后以每件25元的价格处理。乙商店一年后剩下的这种商品第1件按25元的价格处理，第2件按24元的价格处理，第3件按23元的价格处理，依此类推。今年甲、乙两个商店同时购进这种商品40件，根据前5年的销售情况，请你预测哪间商店的期望利润较大？

19、（本小题满分14分）

已知ABC的三个顶点均在椭圆4x² +5y² = 80上，且点A是椭圆与y 轴正半轴的交点。

（1）若ABC的重心是椭圆的右焦点F，试求直线BC的方程；（6分）

（2）若∠A =  ，AD垂直BC于点D，试求点D的轨迹方程。

20、（本小题满分14分）

已知函数且函数 f(x) 的图象关于原点对称，其图象在x = 3 处的切线方程为8x – y – 18 = 0 .

（1）问是否存在区间[ m , n ]，使得函数 f (x) 的定义域和值域均为 [ m , n ]？若存在，求出 f (x) 的解析式和这样的一个区间 [ m , n ]；若不存在，请说明理由；（7分）

（2）设数列 { a _n }满足：，试比较+

与1的大小关系，并说明理由。（7分）

答案

一、　 BACAD　　　CBCDB

二、　11、　48　　　 12、(x – 2 )² + y² = 4　　　  13、　 14、4n – 3

三、解答题

15、解：（1）已知得

　

　 令

综上，所得函数f (x)的图象的对称轴的方程为，对称中心坐标为

，函数的最大、最小值分别是

（2）把y = sinx的图象上所有的点向左平移个单位长度，得到y = sin(x +)的图象，再把后者所有点的横坐标缩短到原来的倍（纵坐标不变）得到 y = sin(2x +)的图象，再把此图象向上平移个单位长度即得函数f (x) = sin(2x +) +的图象。

16、解：（1）由已知得：f ^–1(x) = a^x (x∈R)

　∵ a ∈{ a　 12 < 8a – a² }， ∴a² – 8a +12 < 0 ，即2 < a < 6，

　∴ 函数y = f ^–1(x) = a^x 是增函数；

　(2 )  ,必有 x > 0 ,

① 当0 < x < 时 ,  ，

不等式化为 ，∴ – log_a 2x <1 ,故

log_a 2x > – 1　, ∴ ，此时

② 当时， ，

不等式化为 ，∴　log_a 2 <1 ,这显然成立，此时

③ 当时，

不等式化为 ，∴　log_a 2x <1故x < ，此时；

综上所述知，使命题p为真命题的x的取值范围是{ x　 }.

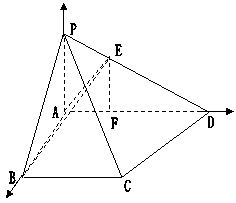
17、解：（1）过点A作AEPD，垂足为E，则点E为所求点.

∵PA⊥平面ABCD

∴AD为PD在平面ABCD上的射影

∵AB⊥AD , AB平面ABCD , ∴ AB⊥PD

而AE⊥PD , AE∩AB = A

∴PD ⊥平面ABE

(2) ∵PA平面ABCD , ∴PA⊥AB , PA⊥AD

又∠ BAD = 90⁰

∴以点为原点建立如图所示的空间直角坐标A – xyz

∵AD∥BC, AB= BC = a　　AD = 2a　

∴A ( 0 , 0 , 0 ) , D ( 0 ,2a , 0 ) , B ( a , 0 , 0 ) , C ( a , a , 0 )

∵PD与底面成30⁰角

∴∠PDA = 30⁰ , PA = 2a　　  ∴P ( 0 , 0 , a )

过E作EF⊥AD于F　　　　 ∵AE⊥PD

又AE = Adsin30⁰ = a ,　 ∴ EF = Aesin60⁰ = a , AF = a

∴E ( 0 , a , a)　 ∴ =　( 0 , a , a) 而 = ( – a , a , 0 )

∴cos< , > =

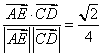
故与所成的角为arccos

18、解：Eξ=10 ×0.15 + 20×0.20 + 30× 0.25 + 40 ×0.30 + 50× 0.10 =30

∴甲商店的期望利润为

30 ×（50 – 30）–（40 – 30 ）×（30 – 25 ）=550 （元）

Eη=40× 0.8 = 32

由题意知，乙商店剩下的产，商品亏本金额是以30 – 25 =5为首项，公差为1，项数为40 – 32 = 8的等差数列。

∴乙商店剩下的亏本金额为

8×5 +×1 = 68（元）

∴乙商店的期望利润为32×（50 – 30）– 68 = 576（元）> 550(元)

答：乙商店的期望利润较大。

19、解：椭圆4x² + 5y² = 80化为，椭圆右焦点F(2 , 0 ) ,A( 0 , 4 )

设B (x₁ , y₁ ) ,C (x₂ , y₂ )，BC中点为M (x ₀ , y₀ )

则K_BC =  , x₁ + x₂ = 2x₀ , y₁ +y₂ = 2y₀

于是有

两式相减有

　　　　　  (1)

又因为F (2 , 0 )为ABC的重心，所以由

代入(1)有 ,

∴直线BC的方程为: 6x – 5y – 28 =0

(2)= (x₁ ,y₁ – 4 ) , = (x₂ ,y₂ – 4 )

∵⊥

∴x₁ x₂ +y₁ y₂ – 4 (y₁ +y₂ ) +16 = 0　　　　　 (2)

设直线BC的方程为y =kx +b ,，代入4x² +5y² =80，得

( 4 +5k²)x² +10kbx +5b² – 80 = 0

∴

把上述各式代入(2)得

 ,　　　∴9b² –32b – 16 = 0

∴b = 4（因点A (0 , 4 )，故舍去）或b =

∴直线BC 经过( 0 , )

设D(x , y )，因AD⊥BC，则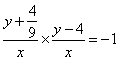　 即 9y² +9x ²– 32y –16 = 0

因ABC三点不共线，所以所求点D的轨迹方程为　

20、解（1）先求f (x )的解析式

　 ∵f (x )的图象关于原点对称，∴f ( – x ) + f (x ) = 0恒成立，即2bx² + 2d = 0恒成立,

∴b = d = 0

又f (x )的图象在x = 3处的切线方程为8x – y – 18 = 0，即y – 6 = 8(x – 3 ),

∴= 8 ,且f ( 3 ) = 6，而f ( x ) = ax³ + cx , =3ax² + c

∴　　解得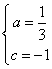

∴f ( x )的解析式为f ( x ) = x³ – x

由题意知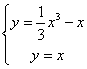　 , 得 x = 0 或 x =

又= x² – 1 , 由= 0，得 x =1 ,

故当x 或 x时， > 0;

当x∈( – 1 , 1 ) 时，< 0.

∴f ( x )在和上单调递增；在[ – 1 , 1] 是单调递减。

∴f ( x )在上的极大值和极小值分别为， , 而，故存在这样的区间[m，n]其中一个区间为

(2)  由(1)知= x² – 1 ,

∴ ，

而函数y=（x + 1）² – 1 = x² +2x 在单调递增 ,

∴由可知， ,

进而可得 ,……由此猜想 .

下面用数学归纳证明：

当n = 1时， ,.结论成立；

假设n = k时，有 ，则当n = k +1时，由y = x² +2x在上递增

可知，即n = k +1时，结论也成立。

对任意的都有，即 ,

∴+++……+≤+++…+=1 – < 1

故+++……+< 1