填 空 题 快 速 解 答

高 锋

　 填空题与选择题都属于客观性试题，具有共同命题的特点，评分客观、公正、准确等，但是基于填空题的特点：与选择题相比，没有备选项。因此，解答时既有不受诱误的干扰，又有缺乏提示的帮助，对考查学生独立思考问题和求解，在能力要求上会更高一些，长期以来，填空题的答对率一直低于选择题的答对率，应该引起同学们的高度重视，而近年来，填空题的题型又有了新的变化和发展，多了一些创新题型，如何才能正确、合理、快速地完成一道填空题？常用的方法有：直接法、数形结合法、特殊值法、分析法、观察法、参数法等。

（一）直接法

　 从题设条件出发，运用定义、定理、公式、性质、法则等知识，通过变形、推理、计算等，得到正确的结论。

　 [例1] 的展开式中的系数为　　　　　　　　　　　 。

　 解：

得展开式中的系数为=179。

　 [类比1] 已知函数在区间上为增函数，则实数的取值范围

是　　　　　　　　　  。

　 [类比2] 函数，在中的最大值比最小值大，则的值

为　　　　　　　　　 。

　 [类比3] 在等差数列中，若，则等式

（）成立，类比上述性质，相应地，在等比数列中，若，则有等

式　　　　　　　　　　　　　　　　　　　　 成立。

　 [类比4] 已知是直线，是平面，给出下列命题：

　 ①若，，，则，或；

　 ②若，，，则；

　 ③若不垂直，则不可能垂直于内无数条直线；

　 ④若，，且，，则且。

　 其中正确的命题的序号是　　　　　　　　  。（注：把你认为正确的命题的序号都填上）

（二）特殊值法

　 根据题设条件的特征，选取恰当的特殊值进行计算，从而得出探求的结论。

　 [例2] 不论取何值，直线恒过一定点，这个定点坐标是　 .

解：取两个值分别代入直线得不同方程为。解得交点坐标为。

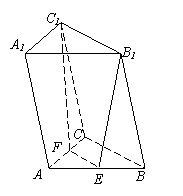
[类比1] 如图所示，三棱柱中，若E、

F分别为AB、AC的中点，平面将三棱柱分成

体积为两部分，则=　　　　　　  。

　 [类比2] 设，且，则直线

通过的定点为　　　　　　　 。

　 [类比3] 若，则

=　　　　　  。

　 [类比4] 已知等差数列的各项均为正数，且满足，

则该数列的前12项之和等于　　　　　　　 。

（三）构造法

  根据题设条件与结论的特殊性，构造出一些新的数学形式，并借助于它认识和解决问题的一种方法。

  [例3] 4个不同的小球放入编号为1，2，3，4的4个盒中，则只有1个空盒的放法共有

　　　　　　 种（用数字作答）。

　 解：符合条件的放法是：有一个盒中放2个球，有2个盒中各放1个球。因此可先将球

分成3堆（一堆2个，其余2堆各1个，即构造了球的“堆”），然后从4个盒中选出3个盒

放1堆球，依分步计算原理，符合条件的放法有（种）。

  [类比1] 在球面上有四个点P、A、B、C，如果PA、PB、PC两两互相垂直，且PA=PB=

PC=，那么这个球面面积是　　　　　　　　　  。

（四）分析法

根据题设条件的特征进行观察、分析，从而得出正确的结论。

[例4] 设含有10个元素的集合全部子集数为，其中由3个元素组成的子集数为，则的值为　　　　　　　　  。

解：由，，故。

[类比1] 设是首项为1的正项数列，且(n=1,2,3,…),

则它们的通项公式是　　　　　　　　　  。

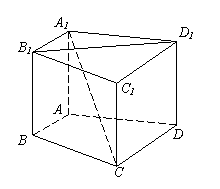　 [类比2] 如右图，在直四棱柱

中，当底面四边形满足条件　　　　　　　　　 

时，有（填上你认为正确的一个条件

即可，不必考虑所有可能性的情形）。

　 [类比3] 椭圆长轴上一个顶点为

A，　以A为直角顶点作一个内接于椭圆的等腰直角

三角形，该三角形的面积是　　　　　　　 。

　 [类比4] 已知函数，给出下列命题：

　 ①必是偶函数；

　 ②时，的图象必关于直线对称；

　 ③若，则在区间上是增函数；

　 ④有最大值。

其中正确的命题的序号是　　　　　　　　　　　　 。

（五）整体代入法

　 将需要解决的问题看作一个整体，通过研究问题的整体形式、整体结构、整体功能或作种种整体处理后，达到顺利而又简捷地解决问题的目的。

　 [例5] 三棱锥的三个侧面两两互相垂直，它们的侧面积分别是6、4、3，则它的体积等于　　　　 。

　 解：设三条棱长分别为，则。

　 得。

　 [类比1] 不等式的解集为　　　　　　　　　　　  。

（六）数形结合法

　 根据题目条件的特点，作出符合题意的图形（象），然后通过对图形的分析而得出正确的结论。

　 [例6] 设对任意实数，函数总有意义，则实数的取值范围是　　　　　　　 　　　 。

　 解：函数有意义，有，

即在时恒成立。

设，则当时，恒成立。

依右图抛物线的特征，有，

得，解得。

　 另解：函数有意义，有，

即在时恒成立。得，运用导数可求得

在时的极大值为4，于是。

　 [类比1] 定义在R上的函数是增函数，是其图象上的两点，则不等式的解集为　　　　　　　　　　　  。

　 [类比2] 对任意实数表示中较小的那个数，若，

，则的最大值是　　　　　　　　 。

　 [类比3] 关于的方程有且只有一个实根，则实数的取值范围是　 。

参考答案

（一）直接法：

1、. 2、. 3、. 4、②⑷.

（二）特殊值法

1、7:5. 2、(1,1). 3、1. 4、48.

（三）构造法

1、.

（四）分析法

1、. 2、. 3、. 4、③.

（五）整体代入法

1、.

（六）数形结合法

1、. 2、1. 3、。

　　　　　　　　　　　　  （柯正摘自《状元之路·高考热点专题专练·数学》北京教育出版社）