高考适应性训练（二）

一、选择题：

1、已知三个平面α、β、γ，α∩β＝a，β∩γ＝b，γ∩α＝c，若a∩b＝M，则直线a，b，c　　 （　　）

A．有一个交点　 　　　　　　　　　 B．有二个不同交点

C．有三个不同交点 　　　　　　　　 D．不确定

2、椭圆的焦点在y轴上，长轴长是短轴长的两倍，则m的值是　　（　　）

A．　　　　　 B．　　　　　　　C．2　　　　　　　 D．4

3、已知正方体八个顶点中，有四个顶点恰好为正四面体的顶点，则该正四面体的体积与正方体的体积之比为　　（　　）

A．　　　　B．1:2　　　　　　 C．2:3　　　　　　 D．1:3

4、已知函数y＝f（x）的反函数是，则方程f（x）＝2003的解集为　　（　　）

A．｛－1｝　　　 B．｛－1，1｝　　　 C．｛1｝　　　　　　D．φ

5、函数y＝f（x－1）的图象如左下图所示，它在R上单调递减，现有如下结论：①f（0）>1　②　③　④，其中正确结论的个数是（　　）

　　　　　　 

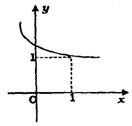
A．1　　　　　　　B．2　　　　　　　 C．3　　　　　　　 D．4

6、如右上图，在正三角形ABC中，D，E，F分别为各边的中点，G，H，I，J分别为AF，AD，BE，DE的中点，将△ABC沿DE，EF，DF折成三棱锥以后，GH与IJ所成角的度数为　　（　）

A．90°　　　　 B．60°　　　　　　C．45°　　　　　　D．0°

7、二次函数f（x）的二次项系数为正，且对任意实数x，恒有f（2＋x）＝f（2－x），若，则x的取值范围是　　（　　）

A．x>2　　　　　B．x<－2或0<x<2　　C．－2<x<0 　　 D．无法确定

二、填空题

8、圆心在直线2x＋y＝0上，且与直线x＋y－1＝0切于点（2，－1）的圆的方程是 ．

9、5名同学参加演讲比赛，决出了第一到第五的名次，评委告诉甲、乙两名同学：“你们都没有拿到冠军，但乙不是最差的”．由此分析这5名同学的排名顺序共有__54_种不同的情况。

10、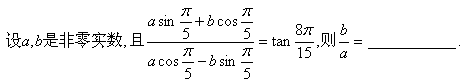

三、解答题：

11、

　　　 （2）求△ABC最短边的长．

　　　　

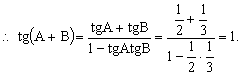
（2）　　  ∴ ∠C所对的边最长，∠B所对的边最短，且为锐角，由，求得，∵ C＝1，

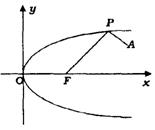
12、如图，F为抛物线的焦点，A（4，2）为抛物线内一定点，P为抛物线上一动点，PA＋PF的最小值为8．

（1）求该抛物线的方程．

（2）若O为坐标原点，问是否存在点M，使过点M的动直线与抛物线交于B，C两点，且∠BOC＝90°，证明你的结论．

（1）

（2）设过定点M的直线方程为y＝kx＋b,显然k≠0，b≠0，直线交抛物线于点B、C．

把直线方程代入抛物线方程得

∴ 动直线方程为y＝kx－16k，即y＝k（x－16），它必过定点（16，0），当不存在时，直线x＝16交抛物线于点B（16，－16），C（16，16）仍有∠BOC＝90°．

∴ 存在定点M（16，0）满足条件．