高考适应性训练（四）

一. 选择题：

1、 函数满足，则f(0)的值为（　　）

　　A. 5　　　　B. 6 　　　 C. -5　　　　　　　D. -6

2、 若a、b为实数，则使成立的一个充要条件为（　　）

　　A. 　　　　　　　B. 　　C. 　　　　　　　　　 D.

3、设a，b，c分别是中∠A，∠B，∠C所对边的边长，则直线与的位置关系是（　　）

　　A. 平行　　　　 B. 重合　　　　 C. 垂直　　　　 D. 相交但不垂直

4、为不共线的向量，且，以下四个向量中模最小者为（　　）

　　A. 　　　　　　 B. 　　C. 　　　　　 D.

5、 已知⊙A：及直线l：，⊙A上到l的距离为3的点共有（　　）

　　A. 1个　　　　　 B. 2个　　　　　 C. 3个　　　　　 D. 4个

6、设a，b是两条异面直线，给出下列四个命题：（1）存在分别经过直线a和b的两个互相平行的平面；（2）存在分别经过直线a和b的两个互相垂直的平面；（3）存在经过直线a与b垂直的平面；（4）存在与a，b都平行且距离相等的平面。其中正确命题的个数是（　　）

　　A. 1个　　　　　 B. 2个　　　　　 C. 3个　　　　　 D. 4个

7、已知是双曲线的左右焦点，P、Q为右支上的两点，直线PQ过且倾斜角为，则的值为（　　）

 A. 　　　　　　 B. 8　　　　C. 　　　　D. 随大小变化

8、正三棱锥中，E为SA的中点，F为的中心，SA＝BC，则异面直线EF与AB所成的角是（　　）

　　A. 　　　　 B. 　　　　　C. 　　　　 D.

9、方程的四个实数根组成一个首项为的等比数列，则（　　）

　　A. 　　　　　　B. 　　　　　 C. 　　　　　　D.

二. 填空题：

10、过直线上一点M向圆作切线，则M到切点的最小距离为。

11、 定点与抛物线上一点P之间的距离为到准线的距离为，当取得最小值时，点P的坐标为__（2，2）__。

12、设向量，规定两向量之间的一个运算为，若已知，则_（-2，1）_。

三. 解答题：

13、如图，在底面是直角梯形的四棱锥中，AD∥BC，∠ABC＝90°，且，又PA⊥平面ABCD，AD＝3AB＝3PA＝3a。

　　（I）求二面角P—CD—A的正切值；

（II）求点A到平面PBC的距离。

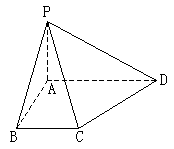
解：（1）在底面ABCD内，过A作AE⊥CD，垂足为E，连结PE

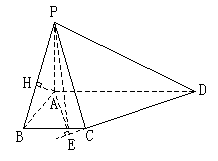
　　∵PA⊥平面ABCD，由三垂线定理知：PE⊥CD

　　∵∠PEA是二面角P—CD—A的平面角………………2分

　　在中，

　　………………4分

　　在中，

　　∴二面角P—CD—A的正切值为………………6分

　　（II）在平面APB中，过A作AH⊥PB，垂足为H

　　∵PA⊥平面ABCD，∴PA⊥BC

　　又AB⊥BC，∴BC⊥平面PAB

　　∴平面PBC⊥平面PAB

　　∴AH⊥平面PBC

　　故AH的长即为点A到平面PBC的距离………………10分

　　在等腰直角三角形PAB中，，所以点A到平面PBC的距离为

14、　已知函数的图象经过原点。

　　（1）若成等差数列，求m的值；

（2）若，正数a、b、c成等比数列，求证：

解：（1）将（0，0）代入，得：　　

由已知可得：　

 即：　（舍）

（2）由已知可得：　　

　　而

　　另解：

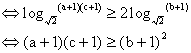
　　∵a，b，c成等比数列

　　　　得证