高考适应性训练(五)
一. 选择题:
1、若奇函数f(x)的定义域为R,则有( )
A.f(x)>f(-x) C.f(x)≤f(-x)
C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
2、若a、b是异面直线,且a∥平面a ,那么b与平面a 的位置关系是( )
A.b∥a B.b与a 相交
C.b![]() a D.以上三种情况都有可能
a D.以上三种情况都有可能
3、若函数f(x)满足![]() ,则f(x)的解析式在下列四式中只有可能是( )
,则f(x)的解析式在下列四式中只有可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、函数y=sinxcotx(0<x<p )的图像的大致形状是(B )
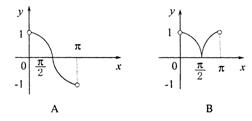
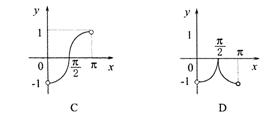
5、若△ABC的内角满足sinA+cosA>0,tanA-sinA<0,则角A的取值范围是( )
A.(0,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,p )
,p )
6、若随机变量x 的分布列如下表,则Ex 的值为( )
| x | 0 | 1 | 2 | 3 | 4 | 5 |
P | 2x | 3x | 7x | 2x | 3x | x |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、我国发射的“神舟3号”宇宙飞船的运行轨道是以地球的中心![]() 为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为( )
为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为( )
A.![]() B.
B.![]()
C.mn D.2mn
8、将函数y=2x的图像按向量![]() 平移后得到函数y=2x+6的图像,给出以下四个命题:①
平移后得到函数y=2x+6的图像,给出以下四个命题:①![]() 的坐标可以是(-3.0);②
的坐标可以是(-3.0);②![]() 的坐标可以是(0,6);③
的坐标可以是(0,6);③![]() 的坐标可以是(-3,0)或(0,6);④
的坐标可以是(-3,0)或(0,6);④![]() 的坐标可以有无数种情况,其中真命题的个数是( )
的坐标可以有无数种情况,其中真命题的个数是( )
A.1 B.2 C.3 D.4
二. 填空题:
9、已知函数![]() 在区间(-1,1)上是增函数,则实数a的取值范围是__ a≥3__.
在区间(-1,1)上是增函数,则实数a的取值范围是__ a≥3__.
10、已知数列{![]() }前n项和
}前n项和![]() 其中b是与n无关的常数,且0<b<1,若
其中b是与n无关的常数,且0<b<1,若![]() 存在,则
存在,则![]() ___1__.
___1__.
三. 解答题:
11、设两个向量![]() 、
、![]() ,满足
,满足![]() =2,
=2,![]() =1,
=1,![]() 、
、![]() 的夹角为60°,若向量
的夹角为60°,若向量![]() 与向量
与向量![]() 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
解析:由已知得![]() ,
,![]() ,
,![]() .
.
∴ ![]() .
.
欲使夹角为钝角,需![]() . 得
. 得 ![]() .
.
设![]() .
.
∴ ![]() ,∴
,∴ ![]() . ∴
. ∴ ![]() ,此时
,此时![]() .
.
即![]() 时,向量
时,向量![]() 与
与![]() 的夹角为p .
的夹角为p .
12、已知数列{![]() }中
}中![]() ,
,![]() (n≥2,
(n≥2,![]() ),数列
),数列![]() ,满足
,满足![]() (
(![]() )
)
(1)求证数列{![]() }是等差数列;
}是等差数列;
(2)求数列{![]() }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)记![]() …
…![]() ,求
,求![]() .
.
解析:(1)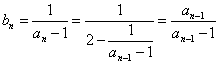 , 而
, 而 ![]() ,
,
∴ ![]() .
.![]()
∴ {![]() }是首项为
}是首项为![]() ,公差为1的等差数列.
,公差为1的等差数列.
(2)依题意有![]() ,而
,而![]() , ∴
, ∴ ![]() .
.
对于函数![]() ,在x>3.5时,y>0,
,在x>3.5时,y>0,![]() ,在(3.5,
,在(3.5,![]() )上为减函数.
)上为减函数.
故当n=4时,![]() 取最大值3。
取最大值3。
而函数![]() 在x<3.5时,y<0,
在x<3.5时,y<0,![]() ,在(
,在(![]() ,3.5)上也为减函数.
,3.5)上也为减函数.
故当n=3时,取最小值,![]() =-1.
=-1.
(3)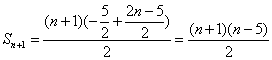 ,
,![]() ,
,
∴ ![]() .
.