2005年高考数学模拟试卷(海门)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M={-1,1,0},N={1,2,3,4,5}, ,映射f:M→N,使对任意的x∈M,都有x+f(x)是奇数,这样的映射f的个数为
A.10 B.11 C.12 D.13
2.现从某校5名学生干部中选出4人分别参加“资源”、“生态”和“环保”三个夏令营,要求每个夏令营活动至少有选出的一人参加,且每人只参加一个夏令营活动,则不同的参加方案的种数是
A.30 B.60 C.120 D.180
3.已知数列![]() 满足:
满足:![]() ,
,![]() ,则
,则![]() 等于
等于
A.2 B.![]() C.
C.![]() D.1
D.1
4.一直线与直二面角的两个面所成的角分别为![]() 、
、![]() ,则
,则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.在抽查某产品尺寸过程中,将其尺寸分成若干组,![]() 是其中的一组,已知该组的频率为
是其中的一组,已知该组的频率为![]() ,该组上的直方图的高为
,该组上的直方图的高为![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.椭圆![]()
![]() 的四个顶点
的四个顶点![]() 、
、![]() 、
、![]() 、
、![]() ,若菱形
,若菱形![]() 的内切圆恰好过焦点,则椭圆的离心率是
的内切圆恰好过焦点,则椭圆的离心率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() 与
与![]() 的图象在
的图象在![]() 上交点的个数是
上交点的个数是
A.3个 B.5个 C.7个 D.9个
9.已知![]() ,
,![]() 曲线
曲线![]() 上一点
上一点![]() 到
到![]() 的距离为11,
的距离为11,![]() 是
是![]() 的中点,
的中点,![]() 为坐标原点,则
为坐标原点,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
10.![]() 是正三棱锥底面内任一点,过
是正三棱锥底面内任一点,过![]() 引底面的垂线与三棱锥三个侧面所在平面交于
引底面的垂线与三棱锥三个侧面所在平面交于![]() 、
、![]() 、
、![]() ,棱锥高为
,棱锥高为![]() ,侧面与底面所成的二面角为
,侧面与底面所成的二面角为![]() ,则
,则![]() 为
为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每答案填在题中横线上。
11.设![]() 是R上以2为周期的奇函数,已知当
是R上以2为周期的奇函数,已知当![]() 时,
时,![]() ,那么
,那么![]() 在
在![]() 上的解析式是 。
上的解析式是 。
 12.已知点
12.已知点![]() 与圆
与圆![]() 上的一点
上的一点![]() ,若
,若![]() ,则
,则![]() 。
。
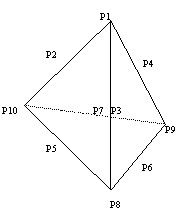
13.如图,点![]() 分别是四面体顶点或棱的中点.那么,在同
分别是四面体顶点或棱的中点.那么,在同
一平面上的四点组![]()
![]()
有 .
14.设函数![]() 的图象为
的图象为![]() ,将
,将![]() 向右平移
向右平移![]() 个单位,
个单位,
可得曲线![]() ,若曲线
,若曲线![]() 与函数
与函数![]() 的图象关于
的图象关于![]() 轴对称,那么
轴对称,那么![]() 可以是
.
可以是
.
三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或或演算步骤.
15.(本小题满分13分)
△ABC的三边为a,b,c,已知![]() ,且
,且![]() ,求三角形面积
,求三角形面积![]() 的最大值.
的最大值.
16.(本小题满分13分)
一出租车司机从饭店火车站途中有![]() 个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是
个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是![]() .
.
(1)求这位司机在途中遇到红灯前,已经通过了![]() 个交通岗的概率;
个交通岗的概率;
(2)设司机在途中遇到![]() 个红灯的概率为
个红灯的概率为![]() ,求
,求![]() 的值.
的值.
17.(本小题满分14分)
四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面是平行四边形,
,底面是平行四边形,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求二面角![]() 的正切值.
的正切值.
18.(本小题满分14分)
对于函数![]() (
(![]() ,
,![]() 为函数的定义域),若同时满足下列条件:①
为函数的定义域),若同时满足下列条件:①![]() 在定义域内单调递增或单调递减;②存在区间
在定义域内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() .那么把
.那么把![]()
![]() 称为闭函数.
称为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]()
![]() 是否为闭函数?并说明理由.
是否为闭函数?并说明理由.
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
19.(本小题满分15分)
已知抛物线![]() 和
和![]() ,如果直线
,如果直线![]() 同时是
同时是![]() 和
和![]() 的切线,称
的切线,称![]() 是
是![]() 和
和![]() 的公切线,公切线上两个切点之间的线段,称为公切线段.
的公切线,公切线上两个切点之间的线段,称为公切线段.
(1)![]() 取什么值时,
取什么值时,![]() 和
和![]() 有且仅有一条公切线?写出此公切线的方程.
有且仅有一条公切线?写出此公切线的方程.
(2)若![]() 和
和![]() 有两条公切线,证明相应的两条切线段互相平分.
有两条公切线,证明相应的两条切线段互相平分.
20.(本小题满分15分)
设函数![]() 的定义域为R,当
的定义域为R,当![]() 时,
时,![]() ,且对任意的实数
,且对任意的实数![]() R,有
R,有![]() 成立.数列
成立.数列![]() 满足
满足![]() ,且
,且![]() (
(![]() N).
N).
(1)求![]() 的值;
的值;
(2)若不等式![]() 对一切
对一切![]() N均成立,求
N均成立,求![]() 的最大值.
的最大值.
参考答案
一、选择题
1.C 2.D 3.A 4.D 5.C 6.C 7.B 8.B 9.B 10.A
二、填空题
11.![]() 12.3 13.33 14.
12.3 13.33 14.![]()
三、解答题
15.解:![]() ,又由余弦定理得
,又由余弦定理得
![]()
![]() .
.![]() ,
,![]() ,得
,得![]() ,
,![]() .又
.又![]() ,
,![]()
![]() .
.
当且仅当![]() 时,等号成立.
时,等号成立.![]()
![]() .
.
16.解(1)司机在途中遇到红灯前,通过了![]() 个交通岗的概率
个交通岗的概率![]()
(2)![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() 17.(1)证:
17.(1)证:![]() ,
,![]() ,
,![]() 为直角,
为直角, 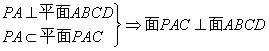
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,取
,取![]() 的中点
的中点![]() ,连
,连![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() 就是异面直线
就是异面直线![]() 与
与![]() 所成的角或补角.
所成的角或补角.
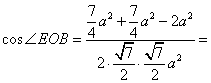
![]() .
.
(3)![]()
![]() 面
面![]() ,过
,过![]() 作
作![]() ,连
,连![]() ,由三垂线定理可知
,由三垂线定理可知![]() ,
,![]()
![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,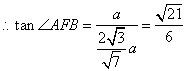 .
.
18.(1)由![]() 在
在![]() 上为减函数,得
上为减函数,得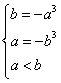 ,可得
,可得![]() ,
,![]() ,
,![]() 所求区间是
所求区间是![]() .
.
(2)取![]() ,
,![]() 可得
可得![]() 不是减函数,取
不是减函数,取![]() ,
,![]() 可得
可得![]() 在
在![]() 不是增函数,所以
不是增函数,所以![]() 不是闭函数.
不是闭函数.
(3)设函数符合条件②的区间为![]() ,则
,则
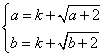 ,故
,故![]() ,
,![]() 是方程
是方程![]() 的两个实根,
的两个实根,
命题等价于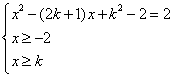 有两个不等实根.
有两个不等实根.
当![]() 时,
时,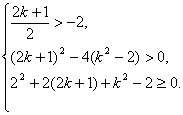 解得
解得![]() ,
,
![]()
![]() ;当
;当![]() 时,
时,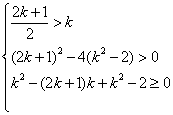 这时,
这时,![]() 无解.
无解.
所以![]() 的取值范围是
的取值范围是![]() .
.
19.(1)函数![]() 的导数
的导数![]() ,曲线
,曲线![]() 在点
在点![]() 的切线方程是:
的切线方程是:
即![]() ,
,
即![]() ①
①
函数![]() 的导数
的导数![]() ,曲线
,曲线![]() 在点
在点![]() 的切线方程
的切线方程
是![]() ,即
,即![]() ②
②
如果直线![]() 是过
是过![]() 和
和![]() 的公切线,则①和②式都是
的公切线,则①和②式都是![]() 的方程,所以
的方程,所以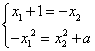 .
.
消去x1,得方程![]() .
.
若判别式![]() 时,即
时,即![]() 时解得
时解得![]() ,此时点
,此时点![]() 与
与![]() 重合.
重合.
即当![]() 时,
时,![]() 和
和![]() 有且仅有一条公切线,由①得公切线方程为
有且仅有一条公切线,由①得公切线方程为![]() .
.
(2)证明:由(Ⅰ)可知,当![]() 时
时![]() 和
和![]() 有两条公切线.
有两条公切线.
设一条公切线上切点为:![]() ,
,![]() .
.
其中![]() 在
在![]() 上,
上,![]() 在
在![]() 上,则有
上,则有![]() ,
,
![]() 。
。
线段![]() 的中点为
的中点为![]() .
.
同理,另一条切线段![]() 的中点也是
的中点也是![]() .
.
所以公切线段![]() 和
和![]() 互相平分.
互相平分.
20.解:(1)令![]() ,
,![]() ,得
,得![]() ,
,![]() ,故
,故![]() .
.
当![]() 时,
时,![]() ,
,![]() ,进而得
,进而得![]() .
.
设![]() R,且
R,且![]() ,
,
则![]() ,
,![]() ,
,![]()
![]() .
.
故![]() ,函数
,函数![]() 在R上是单调递减函数.
在R上是单调递减函数.
由![]() ,得
,得![]() .
.
故![]() ,
,![]() ,
,![]() (
(![]() N)
N)
因此,![]() 是首项为1,公差为2的等差数列.由此得
是首项为1,公差为2的等差数列.由此得![]() ,
,![]() .
.
(2) 由![]() 恒成立,
恒成立,
知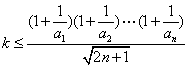 恒成立.
恒成立.
设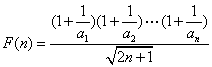 ,则
,则![]() ,
,
且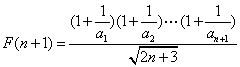 .
.
又![]() ,即
,即![]() ,故
,故![]() 为关于
为关于![]() 的单调增函数,
的单调增函数,![]() .所以,
.所以,![]() ,即
,即![]() 的最大值为
的最大值为![]() .
.