素质能力检测（十一）

一、选择题（每小题5分，共60分）

1.从含有10个元素的集合的全部子集中任取一个，所取的子集是含有3个元素的集合的概率是

A.　　　　　　　　　　　　　 B.　　　　　　　　　　　　　 C.　　　　　　　　　　　　　 D.

解析：含有3个元素的集合个数为C，

所有子集的个数为2¹⁰，

所求概率P==.

答案：D

2.把红、白、黑三张卡片随机地分给甲、乙、丙三人，每人一张，事件“甲分得红牌”与事件“乙分得红牌”是

A.互斥非对立事件　　　　　　　　　　　　　　　　　　　　　　　　 B.对立事件

C.互相独立事件　　　　　　　　　　　　　　　　　　　　　　　D.以上都不对

解析：由定义可得，选A.

答案：A

3.甲、乙两人射击的命中率分别为0.8和0.7，二人同时射击互不影响，结果都命中的概率是

A.0.56　　　　　　　　　　　　　B.0.06　　　　　　　　　　　　　C.0.14　　　　　　　　　　　　　D.0.24

解析：P=0.8×0.7=0.56，选A.

答案：A

4.一批零件10个，其中有8个合格品，2个次品，每次任取一个零件装配机器，若第一次取得合格品的概率是P₁，第二次取得合格品的概率是P₂，则

A.P₁>P₂B.P₁=P₂C.P₁<P₂　　　　　　 D.P₁=2P₂

解析：P₁==，P₂==，所以P₁=P₂.

答案：B

5.袋中有红、黄、白色球各一个，每次任取一个，有放回地抽取3次，则下列事件中概率是的是

A.颜色全同　　　　　　 　　　　　　　　　　　　　　　B.颜色全不同

C.颜色无红色　　　　　　 　　　　　　　　　　　　　 D.颜色不全同

解析：先计算颜色全相同的概率为P==，所以是颜色不全同的概率.

答案：D

6.（2004年江苏模拟题）一个正方体，它的表面涂满了红色.在它的每个面上切两刀，可得27个小立方块，从中任取2个，其中恰有1个一面涂有红色，1个两面涂有红色的概率为

A.　　　　　　　　　　　　 B.　　　　　　　　　　　　 C.　　　　　　　　　　　　　 D.

解析：由=.故选C.

答案：C

7.从1，2，…，6这六个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是

A.　　　　　　　 　B.　　　　　　　 　C.　　　　　　　 　D.

解析：3个数的和为偶数可能都是偶数或2个奇数1个偶数，其取法为C+CC.

∴P==.故选C.

答案：C

8.从3台甲型彩电和2台乙型彩电中任取2台，其中两种品牌齐全的概率是

A.　　　　　　　 　B.　　　　　　　 　C. 　　　　　　　　　　　　　D.

解析：品牌齐全的取法有CC，

故所求概率P==.

答案：C

9.（2004年武汉模拟题）设两个独立事件A和B均不发生的概率为，A发生B不发生的概率与B发生A不发生的概率相同，则事件A发生的概率P（A）是

A.　　　　　　 　B. 　　　　　　　　　　　　　 C.　　　　　　　 　D.

解析：设A、B发生的概率分别为p₁、p₂，

由题意知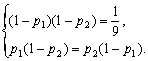

解得p₁=p₂=.故选D.

答案：D

10.（2004年潍坊市模拟题）一次课改经验交流会打算交流试点类学校的论文5篇和非试点类学校的论文3篇.排列次序可任意排列，则最先和最后交流的论文不来自同类学校的概率是

A.　　　　　　　　　　　　　 B.　　　　　　　　　　　　　 C.　　　　　　　　　　　　　 D.

解析：最先和最后交流论文来自不同学校的取法为CCAA.

∴所求概率P==.

答案：B

11.甲袋内装有白球3个、黑球5个，乙袋内装有白球4个、黑球6个.现从甲袋内随机抽取一个球放入乙袋，充分掺混后再从乙袋内随机抽取一个球放入甲袋，则甲袋内白球没有减少的概率为

A.　　　　　　　　　　　　　 B.　　　　　　　　　　　　　 C.　　　　　　　　　　　　　 D.

解析：分两类.（1）若从甲袋取黑球，其白球没有减少的概率P₁=.

（2）若从甲袋中取白球，同样P₂=.

故白球没有减少的概率P=+=+=.

答案：B

12.如果一个人的生日在星期几是等可能的，那么6个人的生日都集中在一个星期中的两天，但不是都在同一天的概率是

A.　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　　　　　　　　　　　　　　　　　　　　　　　　 D.

解析：（1）每个人生日都有7种可能，故共有7⁶种；

（2）集中在两天中，故为C（2⁶－2）（每人生日有两种可能，集中在同一天也为2种）.所以P=，故选A.

答案：A

二、填空题（每小题4分，共16分）

13.（2004年广东，13）某班委会由4名男生与3名女生组成.现从中选出2人担任正副班长，其中至少有1名女生当选的概率是________.（用分数作答）

解析：2名女生当选的取法为C，1名女生当选的取法为CC.

∴概率为=.

答案：

14.（2005年春季上海，6）某班共有40名学生，其中只有一对双胞胎，若从中一次随机抽查三位学生的作业，则这对双胞胎的作业同时被抽中的概率是________.（结果用最简分数表示）

解析：∵抽查三位学生双胞胎在内的方法为C种，

∴P==.

答案：

15.某厂有三个顾问，假定每个顾问发表的意见是正确的概率为0.8.现就某事可行与否征求各顾问的意见，并按顾问中多数人的意见作出决策，作出正确决策的概率是________.

解析：至少有两个顾问作出正确决定即可.

P=C·0.8²·0.2+0.8³=0.896.

答案：0.896

16.六位身高全不相同的同学拍照留念，摄影师要求前后两排各三人，则后排每人均比前排同学高的概率是________.

解析：6位同学共有A种排法，其中后排每人均比前排同学高，共有AA种排法，故其概率为=.

答案：

三、解答题（本大题共6小题，共74分）

17.（12分）已知集合A={－8，－6，－4，－2，0，1，3，5，7}，在平面直角坐标系中，点（x，y）的坐标x∈A，y∈A，且x≠y，计算：

（1）点（x，y）正好在第二象限的概率；

（2）点（x，y）不在x轴上的概率.

解：（1）P₁==.

（2）P₂==（或P₂=1－=.

∴点（x，y）正好在第二象限的概率是，

点（x，y）不在x轴上的概率是.

18.（12分）某商店采用“购物摸球中奖”促销活动，摸奖处袋中装有10个号码为n（1≤n≤10，n∈N*），重量为f（n）=n²－9n+21（g）的球.摸奖方案见下表：

方　案	摸奖办法	奖　金
①	凡一次购物在［50，100］元者，摸球1个，若球的重量小于该球的号码数，则中奖	10元
②	凡一次购物在100元以上者，同时摸出两球，若两球的重量相等，则中奖	40元

说明：凭购物发票到摸奖处，按规定方案摸奖；这些球以等可能性从袋中摸出；假定符合条件的顾客均参加摸奖.

试比较方案①与②的中奖概率的大小.

解：当球的重量小于号码数时，有

n²－9n+21<n，解得3<n<7.

∵n∈N*，∴n的取值为4，5，6.

∴所求的概率为P₁=.

设第n号与第m号的两个球的重量相等，不妨设n<m，则有n²－9n+21=m²－9m+21，

即（n－m）（m+n－9）=0.

∵n≠m，∴m+n=9.

∴（n，m）的取值满足（1，8），（2，7），（3，6），（4，5）.

∴所求的概率为P₂==.

∴P₁>P₂，即方案①的中奖概率大.

19.（12分）如图，电路中4个方框处均为保险匣，方框内数字为通电后在一天内保险丝不被烧断的概率，假定通电后保险丝是否烧断是互相独立的.

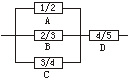
求：（1）通电后电路在一天内A、B恰有一个被烧断的概率；

（2）通电后电路在一天内不断路的概率.

解：以A、B、C、D分别记为各处保险丝不被烧断的事件，则它们的对立事件为、、、，依题意各事件是相互独立的.

（1）通电后电路在一天内A、B恰有一个被烧断包括两种情况：

A被烧断但B不被烧断，即·B事件发生；

A不被烧断但B被烧断，即A·事件发生.

由题意事件·B与A·互斥，

故所求概率为

P（·B+A·）=P（·B）+P（A·）=P（）P（B）+P（A）P（）=（1－）×+×（1－）=.

（2）左电路系统不断路的概率为1－P（··）=1－P（）P（）P（）=1－（1－）（1－）（1－）=.

一天内电路不断路的概率为×=.

20.（12分）某学生骑自行车上学，从家到学校的途中有2个交通岗.假设他在这两个交通岗处遇到红灯的事件是相互独立的，并且概率都是0.6，计算：

（1）2次都遇到红灯的概率；

（2）至少遇到1次红灯的概率.

（1）解：记“他第一次遇到红灯”为事件A，记“他第二次遇到红灯”为事件B.由题知，A与B是相互独立的，因此，“他两次都遇到红灯”就是事件A·B发生.根据相互独立事件的概率乘法公式，得P（A·B）=P（A）·P（B）=0.6×0.6=0.36.

答：他两次都遇到红灯的概率是0.36.

（2）解法一：=“他第一次没有遇到红灯”，=“他第二次没有遇到红灯”.

∴·B=“他第一次没有遇到红灯，第二次遇到红灯”，A·=“他第一次遇到红灯，第二次没有遇到红灯”，并有·B与A·是互斥的，因此，他恰有一次遇到红灯的概率是P（·B+A·）=P（·B）+P（A·）=（1－0.6）×0.6+0.6×（1－0.6）=0.48.

∴他至少遇到1次红灯的概率是P（A·B）+P（·B+A·）=0.36+0.48=0.84.

答：至少遇到1次红灯的概率是0.84.

解法二：=“他第一次没有遇到红灯”，=“他第二次没有遇到红灯”.

∴·=“他两次都没有遇到红灯”，

P（·）=P（）·P（）=（1－0.6）×（1－0.6）=0.16.

∴他至少遇到1次红灯的概率是P=1－P（·）=1－0.16=0.84.

答：至少遇到1次红灯的概率是0.84.

21.（12分）（理）现有5个工人独立地工作，假定每个工人在1小时内平均有12分钟需要电力.

（1）求在同一时刻有3个工人需要电力的概率；

（2）如果最多只能供应3个人需要的电力，求超过负荷的概率.

解：（1）依题意，每名工人在1小时内需要电力的概率是P==.

因此，在同一时刻有3个工人需要电力的概率为P₁=C（）³（）²=0.0512.

（2）超负荷的概率为P₂=C（）⁴（）+C（）⁵=+=0.00672.

（文）甲、乙两个篮球运动员，投篮命中率分别是0.7和0.8，每人投篮两次.

（1）求甲进2球，乙进1球的概率；

（2）若投进1球得2分，未投进得0分，求甲、乙二人得分相等的概率.

解：（1）依题意，所求概率为P₁=C0.7²·C0.8×0.2=0.1568.

（2）甲、乙二人得分相等的概率为

P₂=C0.7²·C0.8²+C0.7×0.3×C0.8×0.2+0.3²×0.2²

=0.3136+0.1344+0.0036

=0.4516.

22.有点难度哟！

（14分）某数学家随身带着甲、乙两盒火柴，每盒有n根，每次用时，随机地任取一盒，然后从中抽取一根（巴拿赫火柴问题）.求：

（1）第一次发现一盒空时，另一盒恰剩r根火柴的概率（r=0，1，…，n）；

（2）第一次用完一盒火柴（不是发现空）时另一盒恰剩r根火柴的概率（r=1，2，…，n）.

分析：第n+1次取到甲盒时，才发现甲盒空，但第n次取甲盒后即已用完甲盒火柴.因此（1）（2）中的两个事件不同.

解：（1）记A=“首次发现一盒空时另一盒恰剩r根火柴”，

B=“首次发现的空盒是甲盒且此时乙盒恰剩r根火柴”，

C=“首次发现的空盒是乙盒且此时甲盒恰剩r根火柴”.

则事件B与C互斥，A=B+C.

由于甲、乙盒所处地位相同，故P（B）=P（C）.

为求P（B），令D=“在甲、乙两盒中任取一盒，得到甲盒”，则P（D）=.

事件B发生相当于独立重复地做了2n－r+1次试验，前2n－r次D恰好发生n次、第2n－r+1次D也发生.

因此P（B）=C（）ⁿ（1－）^n－r·

=C，

P（A）=P（B）+P（C）=2P（B）=C.

（2）记E=“首次用完一盒时另一盒恰有r根”，

F（G）=“首次用完的是甲（乙）盒且此时乙（甲）盒恰有r根火柴”.

则事件F与G互斥，E=F+G.

事件F发生相当于独立重复地做了2n－r次试验，前2n－r－1次D恰好发生n－1次，第2n－r次D也发生.

故P（F）=C（）^n－1（1－）^n－r·=C.

类似（1），P（E）=P（F）+P（G）=2P（F）=C.

评述：改记A为A_r，则A₀，A₁，…，A_n彼此互斥，和是必然事件，故C=1；

改记E为E_r，则E₁，E₂，…，E_n也彼此互斥，和是必然事件，

故C=1.

因此使用概率方法我们可以得到一些恒等式.

（1）中分别取r=0和n，得

P（首次发现一盒空时另一盒也空）=C，

P（首次发现一盒空时另一盒原封未动）=；

（2）中取r=n，得

P（用完一盒时另一盒原封未动）=.