高三数学高考模拟试题
一、选择题(每小题5分,共60分)
1.非空集合A、B满足![]() ,U是全集,则下列式子:①
,U是全集,则下列式子:①![]() ,②
,②![]() ,③(
,③(![]()
![]() )
)![]() B=U,④(
B=U,④(![]()
![]() )
)![]() (
(![]()
![]() )=U中成立的是( ).
)=U中成立的是( ).
A.①,② B.③,④ C.①,②,③ D.①,②,③,④
2.已知![]() =(3,-2),
=(3,-2),![]() =(-5,-1),则
=(-5,-1),则![]()
![]() 等于( ).
等于( ).
A.(8,1) B.(-8,1) C.(-8,-1) D.![]() ,
,![]() )
)
3.函数![]() 的定义域是( ).
的定义域是( ).
A.(2,3) B.[2,![]() C.(2,
C.(2,![]() D.(2,+∞)
D.(2,+∞)
4.如果数列![]() 的前n项和
的前n项和![]() ,那么这个数列( ).
,那么这个数列( ).
A.是等差数列而不是等比数列 B.是等比数列而不是等差数列
C.既是等差数列又是等比数列 D.既不是等差数列又不是等比数列
5.锐二面角![]() 的棱l上一点A,射线
的棱l上一点A,射线![]() ,且与棱成45°角,又AB与
,且与棱成45°角,又AB与![]() 成30°角,则二面角
成30°角,则二面角![]() 的大小是( ).
的大小是( ).
A.30° B.45° C.60° D.90°
6.有6个人分别来自3个不同的国家,每一个国家2人。他们排成一行,要求同一国家的人不能相邻,那么他们不同的排法有( ).
A.720 B.432 C.360 D.240
7.直线经过点A(2,1),B(1,![]() )两点
)两点![]() ,那么直线l的倾斜角取值范围是( ).
,那么直线l的倾斜角取值范围是( ).
A.[0,![]() B.
B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
8.下列函数中同时具有性质:(1)最小正周期是![]() ,(2)图象关于
,(2)图象关于![]() 对称,(3)在
对称,(3)在![]() ,
,![]() 上是增函数的是( ).
上是增函数的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设双曲线![]() 的右准线与两条渐近线交于A、B两点,右焦点为F,且FA⊥FB,则双曲线的离心率为( ).
的右准线与两条渐近线交于A、B两点,右焦点为F,且FA⊥FB,则双曲线的离心率为( ).
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
10.设下表是某班学生在一次数学考试中数学成绩的分布表
| 分数 |
|
|
|
|
|
|
|
|
| 人数 | 2 | 5 | 6 | 8 | 12 | 6 | 4 | 2 |
那么分数在[100,110]中和分数不满110分的频率和累积频率分别是( ).
A.0.18,0.47 B.0.47,0.18 C.0.18,1 D.0.38,1
11.已知![]() ,则以下选项正确的是( ).
,则以下选项正确的是( ).
A.f(3)>f(1)>f(2) B.f(3)>f(1)>f(2)
C.f(3)>f(2)>f(1) D.f(1)>f(3)>f(2)
12.下列各组复合命题中,满足“p或q”为真,“p且q”为假,“非p”为真的是( ).
A.p:0=![]() ,q:0
,q:0![]()
B.p:过空间一点有且仅有一条直线与两异面直线a,b都相交,q:在△ABC中
若![]() ,则A=B
,则A=B
C.p:不等式![]() 的解集为(-∞,0),q:y=
的解集为(-∞,0),q:y=![]() 在第一象限是增函数
在第一象限是增函数
D.p:![]() ,q:椭圆
,q:椭圆![]() 的一条准线方程是x=4
的一条准线方程是x=4
二、填空题(每小题4分,共16分)
13.已知一个球的半径为1,若使其表面积增加到原来的2倍,则表面积增加后球的体积是______________.
14.函数![]() 的单调递减区间是______________.
的单调递减区间是______________.
15.已知![]() 、
、![]() 是实数,给出下列四个论断:(1)
是实数,给出下列四个论断:(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]() ,
,![]() ,(4)
,(4)![]() .以其中的两个论断为条件,其余两个论断作为结论,写出你认为正确的一个命题:________.
.以其中的两个论断为条件,其余两个论断作为结论,写出你认为正确的一个命题:________.
16.一天内的不同的时刻,经理把文件交由秘书打字。每次都将文件堆放在秘书的文件堆的上面,秘书有时间就将文件最上面的那份文件取来打字。若有5份文件,且经理是按1,2,3,4,5的顺序交来的,在下列的顺序①12345,②32415,③24351,④54321,⑤45231中,秘书打字的可能顺序是________(只要填上序号).
三、解答题(第17~21题每题12分,第22题14分,共74分)
17.在△ABC中,已知角A、B、C所对的三边a,b,c成等比数列.
(1)求证:![]() ;
;
(2)求函数![]() 的值域.
的值域.
18.已知等差数列![]() 的首项
的首项![]() ,且公差d>0,第二项、第五项、第十四项分别是等比数列
,且公差d>0,第二项、第五项、第十四项分别是等比数列![]() 的第二项、第三项、第四项.
的第二项、第三项、第四项.
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)设数列![]() 对任意自然数n均有
对任意自然数n均有![]() 成立,求
成立,求![]() 的值.
的值.
19.如图,△ABC中,AC=BC,AE和CD都垂直于平面ABC,且AE=AB=2,F为BE的中点,DF∥平面ABC,
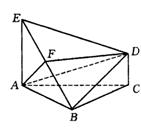
(1)求CD的长;
(2)求证:AF⊥BD;
(3)求平面ADF与平面ABC所成的二面角的大小.
20.袋里装有35个球,每个球上都标有从1到35的一个号码,设号码n的球重![]() (克).这些球以等可能性(不受重量的影响)从袋里取出.
(克).这些球以等可能性(不受重量的影响)从袋里取出.
(1)如果任意取出一球,试求其重量大于号码数的概率;
(2)如果同时任意取出二球,试求它们重量相同的概率.
21.如图:已知△OFQ的面积为![]() ,且
,且![]() ,
,
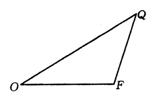
(1)若![]() 时,求向量
时,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() 时,若以O为中心,F为焦点的双曲线经过点Q,当
时,若以O为中心,F为焦点的双曲线经过点Q,当![]() 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
22.已知函数![]() (a、b、
(a、b、![]() )的图象按
)的图象按![]() =(-1,0)平移后得到的图象关于原点对称,f(2)=2,f(3)<3.
=(-1,0)平移后得到的图象关于原点对称,f(2)=2,f(3)<3.
(1)求a、b、c的值;
(2)设![]() ,
,![]() 求证:
求证:![]() ;
;
(3)设x是正实数,求证:![]() .
.
参考答案
1.C 2.D 3.A 4.B 5.B 6.D 7.B 8.C 9.A 10.A
11.A 12.B 13.![]() 14.[-1,3](填(-1,3)也算对)
14.[-1,3](填(-1,3)也算对)
15.①③![]() ②④由①知
②④由①知![]() 与
与![]() 同号,故②成立;再由③得
同号,故②成立;再由③得![]() 故④成立
故④成立
16.①②③④
17.(1)因为a、b、c成等比数列,所以![]() ,由余弦定理得:
,由余弦定理得:![]() ,又因为∠B
,又因为∠B![]() (0,
(0,![]() ),所以0<∠B≤
),所以0<∠B≤![]() . (2)由
. (2)由![]()
![]() ,因为0<∠B≤
,因为0<∠B≤![]() ,所以
,所以![]() ,所以
,所以![]() ,即原函数的值域是(1,
,即原函数的值域是(1,![]()
18.(1)由题意得:![]() ,解得:d=2,所以
,解得:d=2,所以![]() ,易得
,易得![]() . (2)由题意得:
. (2)由题意得:![]() ,所以
,所以![]() ,所以由错项相消法得
,所以由错项相消法得![]()
19.(1)取AB中点G,连FG、CG,则FG∥AE,又AE和CD都垂直于平面ABC,所以AE∥CD,所以FG∥CD,所以F、G、C、D四点共面.又平面![]() 平面ABC=CG,DF∥平面ABC,所以DF∥CG,所以四边形FGCD是平行四边形,所以
平面ABC=CG,DF∥平面ABC,所以DF∥CG,所以四边形FGCD是平行四边形,所以![]() . (2)直角三角形ABE中,AE=AB,F是BE的中点,所以AF⊥BE,又△ABC中,AC=BC,G是AB中点,所以CG⊥AB,又AE垂直于平面ABC,所以AE⊥CG,又
. (2)直角三角形ABE中,AE=AB,F是BE的中点,所以AF⊥BE,又△ABC中,AC=BC,G是AB中点,所以CG⊥AB,又AE垂直于平面ABC,所以AE⊥CG,又![]() ,所以CG⊥面ABE.因为DF∥CG,所以DF⊥面ABE,所以AF⊥DF,又因为
,所以CG⊥面ABE.因为DF∥CG,所以DF⊥面ABE,所以AF⊥DF,又因为![]() ,所以AF⊥面BED,所以AF⊥BD. (3)设面
,所以AF⊥面BED,所以AF⊥BD. (3)设面![]() 面ABC=L,因为DF∥平面ABC,所以DF∥L,又DF⊥面ABE,所以L⊥面ABE,所以L⊥AF,L⊥AB,所以∠FAB即为二面角的平面角.直角三角形ABE中,易得∠FAB=45°,所以平面ADF与平面ABC所形成的较小的二面角为45°
面ABC=L,因为DF∥平面ABC,所以DF∥L,又DF⊥面ABE,所以L⊥面ABE,所以L⊥AF,L⊥AB,所以∠FAB即为二面角的平面角.直角三角形ABE中,易得∠FAB=45°,所以平面ADF与平面ABC所形成的较小的二面角为45°

20.(1)由不等式![]() 得n>15,n<3,由题意知n=1,2,或n=16,17,…,35.于是所求概率为
得n>15,n<3,由题意知n=1,2,或n=16,17,…,35.于是所求概率为![]() (2)设第n号与第m号的两个球的重量相等,其中n<m,则有
(2)设第n号与第m号的两个球的重量相等,其中n<m,则有![]() ,所以
,所以![]() ,因为n≠m,所以n+m=15,(n,m)=(1,14),(2,13),…(7,8),但从35个球中任取两个的方法数为
,因为n≠m,所以n+m=15,(n,m)=(1,14),(2,13),…(7,8),但从35个球中任取两个的方法数为![]() ,故,所求概率为
,故,所求概率为![]()
21.(1)由已知,得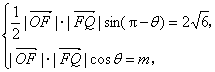 所以
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,则
,则![]() . (2)以O为原点,
. (2)以O为原点,![]() 所在直线为x轴建立直角坐标系,设所求的双曲线方程为
所在直线为x轴建立直角坐标系,设所求的双曲线方程为![]() ,(a>0,b>0),Q点的坐标为(
,(a>0,b>0),Q点的坐标为(![]() ,
,![]() ),则
),则![]() =(
=(![]() ,
,![]() ),因为△OFQ的面积
),因为△OFQ的面积![]() ,所以
,所以![]() ,又由
,又由![]() (c,0)(
(c,0)(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,
,![]() ,当且仅当c=4时,
,当且仅当c=4时,![]() 最小,此时Q的坐标为(
最小,此时Q的坐标为(![]() ,
,![]() ),由此可得
),由此可得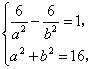 解之得
解之得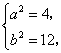 故所求的方程为
故所求的方程为![]()
22.(1)函数f(x)的图象按![]() (-1,0)平移后得到的图象的函数式为
(-1,0)平移后得到的图象的函数式为![]() ,因为其图象关于原点对称,所以
,因为其图象关于原点对称,所以![]() ,即
,即![]() ,因为
,因为![]() N,所以
N,所以![]() >0,所以-bx+c=-bx-c,所以c=0,又因为f(2)=2,所以
>0,所以-bx+c=-bx-c,所以c=0,又因为f(2)=2,所以![]() ,a+1=2b,a=2b-1……①,又
,a+1=2b,a=2b-1……①,又![]() ,4a+1<6b……②,由①②及a、b
,4a+1<6b……②,由①②及a、b![]() N得a=1,b=1. (2)
N得a=1,b=1. (2)![]() ,所以
,所以![]() ,
,![]()
![]() ,当且仅当
,当且仅当![]() =1时,上式取等号,但0<
=1时,上式取等号,但0<![]() <1,0<
<1,0<![]() ≤1,所以
≤1,所以![]() ≠1,
≠1,![]() >2,
>2,![]()
![]() ,当
,当![]() 时,上式=
时,上式=![]() ≤4;当
≤4;当![]() 时,上式=
时,上式=![]() <4,所以
<4,所以![]()
![]() ,即
,即![]() ; (3)
; (3)![]()
![]()
![]()
![]()
![]() ,令
,令![]() ,又
,又![]()
![]() ,所以
,所以![]()
![]()
![]()
![]()
![]()
