专题考案(4)向量板块 第1课 向量的坐标表示

(时间：90分钟　满分：100分)

题型示例

已知点O是△ABC内一点，∠AOB=150°,∠BOC=90°,设=a, =b,=c,且a=2,b=1,c=3,试用a和b表示c.

分析　本例是用平面内两个不共线的向量表示同一平面内的另一个向量.根据平面向量的基本定理有c=λ₁a+λ₂b,当a、b、c的坐标已知时，该式实际上是一个关于λ₁、λ₂的二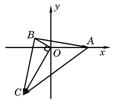元一次方程组，由此可确定λ₁、λ₂，这也是解决本题的一个重要思路.

解：如图1所示，以点O为原点，为x轴的非负半轴，

建立平面直角坐标系.由三角函数的定义，得B(cos150°,sin150°),

图1

C(3cos 240°,3sin 240°),即B(-,),C(-,-).

∴a=(2,0),b=(-,),c=(-,-).设c=λ₁a+λ₂b (λ₁,λ₂∈R)，

则得(-,-)=λ₁(2,0)+λ₂(-，)=(2λ₁-λ₂,λ₂).

∴解得λ₁=-3,λ₂=-3.∴c=-3a-3b.

一、选择题(8×3′＝24′)

1．已知向量=(3,-2),=(-5,-1),则等于 　　　　　　　　　　　　　　　(　　)

A.(-8,1)　　　  B.(8,-1)　　　 C.(4,3)　　　 D.(-3,-4)

2．若向量a=(1,1),b=(1,-1),c=(-1,2)，则c等于　　　　　　　　　　　　　　　　 (　　)

A.-a+b　　 B.a-b　　 C.a-b　　 D.-a+b

3．若a、b是不共线的两个向量，且=λ₁a+b,=a+λ₂b(λ₁、λ₂∈R)，则A、B、C三

点共线的充要条件是　　　　　　　　　  　　　　　　　　　　　　　　　　 (　　)

A.λ₁=λ₂=-1　　　　　 B.λ₁=λ₂=1

C.λ₁λ₂+1=0　　　　　 D.λ₁λ₂-1=0

4．若平面向量b与向量a=(1,-2)的夹角是180°,且b=3,则b等于　　　　　　  (　　)

A.(-3,6)　　　 B.(3,-6)　　  C.(6,-3)　　　 D.(-6,3)

5．已知平面上直线l的方向向量e=,点O(0，0)和A(1，－2)在l上的射影分别是

O′和A′,则=λe,其中λ为　　　　　　　　　　　　　　　　　　　　 (　　)

A.　　　　  B. 　　　　　C.2　　　　  D.-2

6．已知a=(-1,3),b=(x,-1),且a∥b，则x等于　　　　　　　 (　　)

A.3　　　　  B.　　　　　 C.-3　　　　  D.-

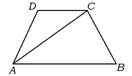
7．如图2，在梯形ABCD中，AB∥DC，且AB=λDC，

图2

若=a,=b,则等于　　　　　　　　　　　　　 (　　)

A.λa+b　　　B.a+λb　　  C.a+b　　　D.a+b

8．已知点A(2,3),B(-2,6),C(6,6),D(10,3)上的A,B,C,D为顶点的四边形是　　　　　 (　　)

A.梯形　　　　 B.邻边不等的平行四边形

C.菱形　　　　 D.两组对边均不平行的四边形

二、填空题(3×4′＝12′)

9．已知a=(3,-2),b=(-4,-3),c=(-5,2),且c=2a+b-3γ，则γ=　　　 .

10．已知a=(6,2),b=(-4,-),直线l过点A(3,-1)且与向量a+2b垂直，则直线l的方程为　　 .

11．已知向量a=(cosθ,sinθ)，向量b=(,-1)，则2a-b的最大值是　　　　.

三、解答题(4×10′＋2×12′＝64′)

12．已知向量a=(x²+y²，xy),b=(5,2)，若a=b，求x、y．

13．用向量方法证明：半径和圆心距均为1的两个圆⊙O₁、⊙O₂，在第一个圆的圆周上任取一点A，在第二个圆的圆周上取关于两圆连心线对称的两个点B₁、B₂.求证：≥2,并指明等号成立的条件.

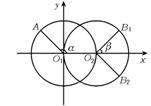
证明：如图3,建立直角坐标系,设∠AO₁x=α(0≤α<2π),

∠B₁O₂x=β(0<β<π),则∠xO₂B₂=-β,又O₁O₂=1,则点A、B₁、B₂

三点坐标分别为A(　　,　　)、B₁(　　，　　)、B₂(　　,　　),

图3

∴=(　  ,　　),=(　  ,　　).∴²=　　 ,²=　　 .

从而=　　　　  ，∴≥2,且当　　　 时取等号.

14．试判断点A(0,-3),B(1,-1),C(2,1)是否共线.

15．平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1),

解答下列问题:

(1)求3a+b-2c;

(2)求满足a=mb+nc的实数m,n;

(3)若(a+kc)∥(2b-a),求实数k;

(4)设d=(x,y)满足(d-c)∥(a+b)且d-c=1,求d.

16．已知△ABC中,A(7,8),B(3,5),C(4,3),M、N分别是AB、AC的中点,D是BC的中点,MN与

AD交于点F,求.

17．已知点A(4,0),B(5,5),C(2,6),AC与OB的交点为P,求交点P的坐标.

参考答案

1．A　=(-5,-1)-(3,-2)=(-8,1).

2．B　设(-1,2)=x(1,1)+y(1,-1), 则.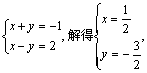

3．D　存在x∈R，使=x，∴得λ₁λ₂=1.

4．A　设b＝（x,y）,由a·b=abcosa,b得:x-2y=x-2y=-15,观察知只有A项正确.

5．D　如图4观察与e必相反，∴λ<0,排除选项A、C.

l的方向向量e=知，方向向上且k_e=-,设l:y=-x3x+4y=0,

图4

则A到l的距离d==1,且OA=.

由勾股定理知OA′==2.∴λ=-2.

6．B　.

7．C　AB∥DC，AB=λDC，=a，∴a．

8．B　=(-4,3),=(-4,3),=(8,0)，=(8,0).

9．(,-3)　3γ=2a+b-c=(6,-4)+(-4,-3)-(-5,2)=(2,-7)-(-5,2)=(7,-9).∴γ=(,-3).

10．2x-y-7=0　a+2b=(-2,1),∴k_l=2,l的方程为y+1=2(x-3),即2x-y-7=0.

11．4　2a-b=(2cosθ,2sinθ)-（,-1）=(2cosθ-,1+2sinθ).

∴2a-b==-1时，2a-b_max=4.

12．解　∵a=b,∴且xy同号，即x=2，y=1或x=-2,y=-1；或x=1,y=2或x=-1,y=-2.

13．解　据题意得　A(cosα,sinα)、B₁（1+cosβ,sinβ）、B₂(1+cosβ,-sinβ),

∴=(1+cosβ-cosα,sinβ-sinα),=(1+cosβ-cosα,-sinβ-sinα).

²=(1+cosβ-cosα)²+(sinβ-sinα)²,²=(1+cosβ-cosα)²+(sinβ+sinα)².

∴=(1+cosβ-cosα)²+(sinβ-sinα)²+(1+cosβ-cosα)²+(sinβ+sinα)²=2+4(1+cosβ)(1-cosα),

∵1+cosβ>0,1-cosα≥0,∴≥2,当α=0时取等号.

14．分析　以三个点中的任何两个作向量，看是否平行，然后证明三点共线.

解　∵=(1,-1)-(0,-3)=(1,2),=(2,1)-(0,-3)=(2,4)=2(1,2)=2,∴∥.

又∵直线AB、AC有公共点A,∴A、B、C三点共线.

15．解　(1)3a+b-2c=3(3,2)+(-1,2)-2(4,1)=(0,6).

(2)∵a=mb+nc,∴(3,2)=m(-1,2)+n(4,1)=(-m+4n,2m+n).∴

(3)∵(a+kc)∥(2b-a),又a+kc=(3+4k,2+k),2b-a=(-5,2),∴2×(3+4k)-(-5)×(2+k)=0,∴k=-.

(4)∵d-c=(x-4,y-1),a+b=(2,4),又(d-c)∥(a+b)且d-c=1,

∴

∴d=或d=.

点评　熟悉向量的线性运算，直接用坐标运算求解，在(3)的求解中,也可用共线条件引入参数求解.在(4)的求解中，对方程求解可将x-4,y-1分别看成整体来对待，有利于求解.

16．解　∵A(7,8),B(3,5),C(4,3),∴=(-4,-3),=(-3,-5).

又∵D是BC中点，有=(+)=(-3.5,-4),而M、N分别为AB、AC的中点，所以F为AD的中点，故有=(,2).

17．解　设=λ(5,5)=(5λ,5λ),则=(5λ-4,5λ),=(-2,6).

∵∥,∴(5λ-4)·6-5λ·(-2)=0,解得λ=,∴=(5,5)=(3,3).

∴点P坐标为(3,3).