2005年高考题分章节汇编
第九章 直线、平面、简单几何体
一、选择题
1.(2005年春考·北京卷·理3)有如下三个命题:
①分别在两个平面内的两条直线一定是异面直线;
②垂直于同一个平面的两条直线是平行直线;
③过平面![]() 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面![]() 垂直.
垂直.
其中正确命题的个数为 ( C )
A.0 B.1 C.2 D.3
2.(2005年春考·北京卷·文3)下列命题中,正确的是 ( C )
A.经过不同的三点有且只有一个平面
B.分别在两个平面内的两条直线一定是异面直线
C.垂直于同一个平面的两条直线是平行直线
D.垂直于同一个平面的两个平面平行
3. (2005年春考·上海卷13)已知直线![]() 及平面
及平面![]() ,下列命题中的假命题是 ( D )
,下列命题中的假命题是 ( D )
A.若![]() ,
,![]() ,则
,则![]() . B.若
. B.若![]() ,
,![]() ,则
,则![]() .
.
C.若![]() ,
,![]() ,则
,则![]() . D.若
. D.若![]() ,
,![]() ,则
,则![]() .
.
4.(2005年高考·北京卷·理6文7)在正四面体P—ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是 ( C )
A.BC//平面PDF B.DF⊥PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
5.(2005年高考·福建卷·理4文7)已知直线m、n与平面![]() ,给出下列三个命题:
,给出下列三个命题:
①若![]() ②若
②若![]()
③若![]() 其中真命题的个数是 ( C )
其中真命题的个数是 ( C )
A.0 B.1 C.2 D.3
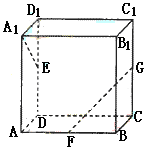 6.(2005年高考·福建卷·理8理11)如图,长方体ABCD—A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是( D )
6.(2005年高考·福建卷·理8理11)如图,长方体ABCD—A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.(2005年高考·广东卷4)已知高为3的直棱柱ABC—A′B′C′的底面是边长为1的正三角形(如图1所示),则三棱锥B′—ABC的体积为( D )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(2005年高考·广东卷7)给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:
①若![]() ;
;
②若m、l是异面直线,![]() ;
;
③若![]() ;
;
④若![]()
其中为假命题的是 ( C )
A.① B.② C.③ D.④
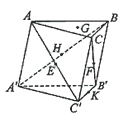 9.(2005年高考·湖北卷·理10)如图,在三棱柱ABC—A′B′C′中,点E、F、H、 K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心. 从K、H、G、B′中取一点作为P, 使得该棱柱恰有2条棱与平面PEF平行,则P为
( C )
9.(2005年高考·湖北卷·理10)如图,在三棱柱ABC—A′B′C′中,点E、F、H、 K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心. 从K、H、G、B′中取一点作为P, 使得该棱柱恰有2条棱与平面PEF平行,则P为
( C )
A.K B.H C.G D.B′
10.(2005年高考·湖北卷·文8)已知a、b、c是直线,![]() 是平面,给出下列命题:①若
是平面,给出下列命题:①若![]() ; ②若
; ②若![]() ;
;
③若![]() ; ④若a与b异面,且
; ④若a与b异面,且![]() 相交;
相交;
⑤若a与b异面,则至多有一条直线与a,b都垂直.
其中真命题的个数是 ( A )
A.1 B.2 C.3 D.4
11.(2005年高考·湖北卷·文5)木星的体积约是地球体积的![]() 倍,则它的表面积约是地球表面积的 ( C )
倍,则它的表面积约是地球表面积的 ( C )
A.60倍 B.60![]() 倍 C.120倍 D.120
倍 C.120倍 D.120![]() 倍
倍
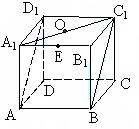
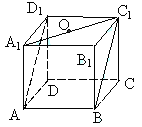 12.(2005年高考·湖南卷·理5)如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面AB C1D1的距离为 (B)
12.(2005年高考·湖南卷·理5)如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面AB C1D1的距离为 (B)
A.![]() B.
B.![]()
 C.
C.![]() D.
D.![]()
13.(2005年高考·湖南卷·文4)如图,正方体ABCD-A1B1C1D1的棱长为1,E是A1B1的中点,则E到平面AB C1D1的距离为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
14.(2005年高考·辽宁卷4)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:①若![]() ; ②若
; ②若![]() ;
;
③若![]() ; ④若m、n是异面直线,
; ④若m、n是异面直线,![]() ,其中真命题是 ( D )
,其中真命题是 ( D )
A.①和② B.①和③ C.③和④ D.①和④
15.(2005年高考·江西卷·理9文9)矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B—AC—D,则四面体ABCD的外接球的体积为 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.(2005年高考·重庆卷·理7)对于不重合的两个平面![]() 与
与![]() ,给定下列条件:
,给定下列条件:
①存在平面![]() ,使得
,使得![]() 、
、![]() 都垂直于
都垂直于![]() ;
;
②存在平面![]() ,使得
,使得![]() 、
、![]() 都平行于
都平行于![]() ;
;
③![]() 内有不共线的三点到
内有不共线的三点到![]() 的距离相等;
的距离相等;
④存在异面直线l、m,使得l//![]() ,l//
,l//![]() ,m//
,m//![]() ,m//
,m//![]() ,
,
其中,可以判定![]() 与
与![]() 平行的条件有 ( B )
平行的条件有 ( B )
A.1个 B.2个 C.3个 D.4个
17.(2005年高考·重庆卷·文7)对于不重合的两个平面![]() ,给定下列条件:
,给定下列条件:
①存在平面![]() ,使得α、β都垂直于
,使得α、β都垂直于![]() ;
;
②存在平面![]() ,使得α、β都平行于
,使得α、β都平行于![]() ;
;
③存在直线![]() ,直线
,直线![]() ,使得
,使得![]() ;
;
④存在异面直线l、m,使得![]()
其中,可以判定α与β平行的条件有 ( B )
A.1个 B.2个 C.3个 D.4个
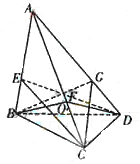 18.(2005年高考·重庆卷·理10)如图,在体积为1的三棱锥A—BCD侧棱AB、AC、AD上分别取点E、F、G, 使AE : EB=AF : FC=AG : GD=2 : 1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O—BCD的体积等于 ( C )
18.(2005年高考·重庆卷·理10)如图,在体积为1的三棱锥A—BCD侧棱AB、AC、AD上分别取点E、F、G, 使AE : EB=AF : FC=AG : GD=2 : 1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O—BCD的体积等于 ( C )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
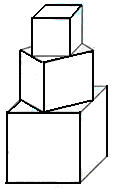 19.(2005年高考·重庆卷·文10)有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各连接中点,已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
( C )
19.(2005年高考·重庆卷·文10)有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各连接中点,已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
( C )
A.4 B.5 C.6 D.7
20.(2005年高考·江苏卷4)在正三棱柱ABC-A1B1C1中,若AB=2,A A1=1,则点A到平面A1BC的距离为 (B)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
21.(2005年高考·江苏卷8)设![]() 为两两不重合的平面,
为两两不重合的平面,![]() 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,则
,则![]() 。
。
其中正命题的个数为 (B)
A.1 B.2 C.3 D.4
22.(2005年高考·浙江卷·理6文7)设![]() 、
、![]() 为两个不同的平面,l、m为两条不同的直线,且l
为两个不同的平面,l、m为两条不同的直线,且l![]()
![]() ,m
,m![]()
![]() ,有如下的两个命题:①若
,有如下的两个命题:①若![]() ∥
∥![]() ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则![]() ⊥
⊥![]() .那么
.那么
(D)
A. ①是真命题,②是假命题 B. ①是假命题,②是真命题
C. ①②都是真命题 D. ①②都是假命题
23.(2005年高考·山东卷·理8文9)设地球的半径为![]() ,若甲地位于北纬
,若甲地位于北纬![]() 东经
东经![]() ,乙地位于南纬
,乙地位于南纬![]() 东经
东经![]() ,则甲、乙两地的球面距离为 ( D )
,则甲、乙两地的球面距离为 ( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
24.(2005年高考·天津卷·理4文5)设![]() 为平面,
为平面,![]() 为直线,则
为直线,则![]() 的一个充分条件是 ( D )
的一个充分条件是 ( D )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
25.(2005年高考·全国卷Ⅰ·理2文2)一个与球心距离为1的平面截球所得的圆面面积为![]() ,则球的表面积为 ( C )
,则球的表面积为 ( C )
A.8![]() B.8
B.8![]() C.4
C.4![]() D.4
D.4![]()
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
27.(2005年高考·全国卷Ⅰ·理11)过三棱柱任意两个顶点的直线共15条,其中异面直线有
( B )
A.18对 B.24对 C.30对 D.36对
28.(2005年高考·全国卷II·理2文2)正方体ABCD—A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点.那么,正方体的过P、Q、R的截面图形是 ( D )
A.三角形 B.四边形 C.五边形 D.六边形
29.(2005年高考·全国卷II·理12)将半径都为1的4个铅球完全装人形状为正四面体的容品里,这个正四面体的高最小值为 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
30.(2005年高考·全国卷Ⅲ·理4文4)设三棱柱ABC—A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B—APQC的体积为 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
31.(2005年高考·全国卷Ⅲ·理11文11)不共面的四个定点到平面![]() 的距离都相等,这样的平面
的距离都相等,这样的平面![]() 共有 ( D )
共有 ( D )
A.3个 B.4个 C.6个 D.7个
 二、填空题
二、填空题
1.(2005年春考·北京卷·理12文12)如图,正方体![]() 的棱长为
的棱长为![]() ,将该正方体沿对角面
,将该正方体沿对角面![]() 切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为__________.
切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为__________.![]()
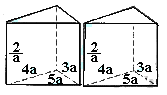 2.(2005年高考·上海卷·理11文12)有两个相同的直三棱柱,高为
2.(2005年高考·上海卷·理11文12)有两个相同的直三棱柱,高为![]() ,底面三角形的三边长分别为
,底面三角形的三边长分别为![]() .用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则
.用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则![]() 的取值范围是__________.
的取值范围是__________.![]()
3.(2005年高考·湖南卷·文15)已知平面![]() 和直线,给出条件:①
和直线,给出条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
(i)当满足条件
时,有![]() ;(ii)当满足条件
时,有
;(ii)当满足条件
时,有![]() .
.
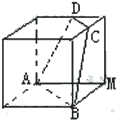 (填所选条件的序号)③⑤ ②⑤
(填所选条件的序号)③⑤ ②⑤
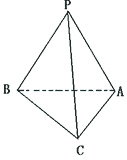
4.(2005年高考·辽宁卷14)如图,正方体的棱长为1,C、D分别是两条棱的中点,
A、B、M是顶点,那么点M到截面ABCD的距离是
. ![]()
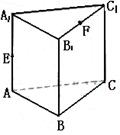 5.(2005年高考·江西卷·理15)如图,在直三棱柱ABC—A1B1C1中,AB=BC=
5.(2005年高考·江西卷·理15)如图,在直三棱柱ABC—A1B1C1中,AB=BC=![]() ,BB1=2,
,BB1=2,![]() ,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
.
,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
. ![]()
6.(2005年高考·江西卷·文15)如图,在三棱锥P—ABC中,PA=PB=PC=BC,且![]() ,则PA与底面ABC所成角为 .
,则PA与底面ABC所成角为 .![]()
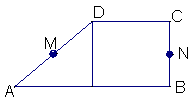 7.(2005年高考·浙江卷·理12文12)设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
7.(2005年高考·浙江卷·理12文12)设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.![]()
8.(2005年高考·山东卷·理16文16)已知![]() 是不同的直线,
是不同的直线,![]() 是不重合的平面,给出下列命题:①若
是不重合的平面,给出下列命题:①若![]() 则
则![]()
②若![]() 则
则![]()
③若![]() ,则
,则![]()
④![]() 是两条异面直线,若
是两条异面直线,若![]() ,则
,则![]()
 上面的命题中,真命题的序号是
上面的命题中,真命题的序号是![]() (写出所有真命题的序号)③④
(写出所有真命题的序号)③④
9.(2005年高考·天津卷·理12文13)如图,PA⊥平面ABC,∠ABC=90°且PA=AC=BC=a,则异面直线PB与AC所成角的正切值等于_______ _.![]()
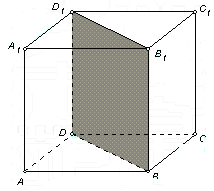
11.(2005年高考·全国卷Ⅰ·理16文16)在正方体ABCD—A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
①四边形BFD′E一定是平行四边形.
②四边形BFD′E有可能是正方形.
③四边形BFD′E在底面ABCD内的投影一定是正方形.
④平面BFD′E有可能垂直于平面BB′D.
以上结论正确的为 .(写出所有正确结论的编号)①③④
12.(2005年高考·全国卷II·理16文16)下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.其中,真命题的编号是 (写出所有真命题的编号). ①,④
三、解答题
 1.(本小题满分14分)(2005年春考·北京卷·理16)
1.(本小题满分14分)(2005年春考·北京卷·理16)
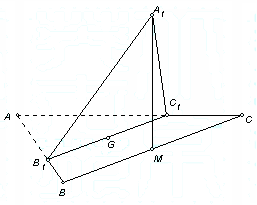
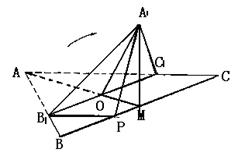
如图,正三角形ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于![]() 、
、![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使点
的位置,使点![]() 在平面
在平面![]() 上的射影恰是线段BC的中点M.求:
上的射影恰是线段BC的中点M.求:
(1)二面角![]() 的大小;
的大小;
 (2)异面直线
(2)异面直线![]() 与
与![]() 所成角的大小(用反三角函数表示).
所成角的大小(用反三角函数表示).
本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
解(Ⅰ)连接AM,A1G
∵G是正三角形ABC的中心,
且M为BC的中点,
∴A,G,M三点共线,AM⊥BC.
∵B1C1∥BC,
∴B1C1⊥AM于G,
即GM⊥B1C1,GA1⊥B1C1,
∴∠A1GM是二面角A1—B1C1—M的平面角.
∵点A1在平面BB1C1C上的射影为M,
∴A1M⊥MG,∠A1MG=90°
在Rt△A1GM中,由A1G=AG=2GM得∠A1GM=90°
即二面角A1—B1C1—M的大小是60°
(Ⅱ)过B1作C1C的平行线交BC于P,则∠A1B1P等于异面直线A1B1与CC1所成的角.
由PB1C1C是平行四边形得B1P=C1C=1=BP,
PM=BM—BP=![]() A1B1=AB1=2.
A1B1=AB1=2.
∵A1M⊥面BB1C1C于M,
∴A1M⊥BC,∠A1MP=90°.
在Rt△A1GM中,A1M=A1G·![]()
在Rt△A1MP中,![]()
在△A1B1P中,由余弦定理得
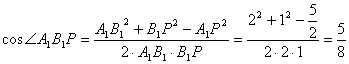 ,
,
∴异面直线A1B1与CC1所成角的大小为arccos![]()
 2.(本小题满分14分)(2005年春考·北京卷·文16)
2.(本小题满分14分)(2005年春考·北京卷·文16)
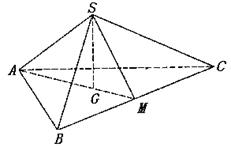
如图,正三棱锥S—ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ)二面角S—BC—A的大小;
(Ⅲ)正三棱锥S—ABC的体积.
 本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
解:(Ⅰ)∵SB=SC,AB=AC,M为BC中点,
∴SM⊥BC,AM⊥BC.
由棱锥的侧面积等于底面积的2倍,即
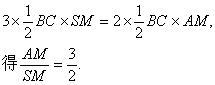
(Ⅱ)作正三棱锥的高SG,则G为正三角形ABC的中心,G在AM上,![]()
∵SM⊥BC,AM⊥BC,
∴∠SMA是二面角S—BC—A的平面角.
在Rt△SGM中,
∵![]()
∴∠SMA=∠SMG=60°,
即二面角S—BC—A的大小为60°。
(Ⅲ)∵△ABC的边长是3,
∴![]()
∴![]()
3. (本题满分14分) (2005年春考·上海卷19)本题共有2个小题,第1小题满分6分,第2小题满分8分.
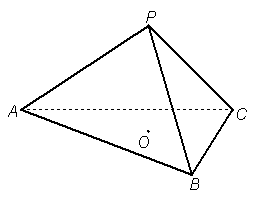
已知正三棱锥![]() 的体积为
的体积为![]() ,侧面与底面所成的二面角的大小为
,侧面与底面所成的二面角的大小为![]() .
. (1)证明:
(1)证明:![]() ;
;
(2)求底面中心![]() 到侧面的距离.
到侧面的距离.
[证明](1)取![]() 边的中点
边的中点![]() ,连接
,连接![]() 、
、![]() ,
,
则![]() ,
,![]() ,故
,故![]() 平面
平面![]() .
…… 4分
.
…… 4分
∴ ![]() .
…… 6分
.
…… 6分
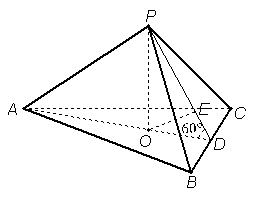 [解](2)如图, 由(1)可知平面
[解](2)如图, 由(1)可知平面![]() 平面
平面![]() ,则
,则![]() 是侧面与底面所成二面角的平面角.
是侧面与底面所成二面角的平面角.
过点![]() 作
作![]() 为垂足,则
为垂足,则![]() 就是点
就是点![]() 到侧面的距离.
…… 9分
到侧面的距离.
…… 9分
设![]() 为
为![]() ,由题意可知点
,由题意可知点![]() 在
在![]() 上,
上,
∴ ![]() ,
,![]() .
.
![]() , …… 11分
, …… 11分
∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() .
.
即底面中心![]() 到侧面的距离为3.
…… 14分
到侧面的距离为3.
…… 14分
4.(本小题共14分)(2005年高考·北京卷·理16)
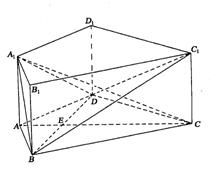 如图,在直四棱柱ABCD—A1B1C1D1中,AB=AD=2,DC=
如图,在直四棱柱ABCD—A1B1C1D1中,AB=AD=2,DC=![]() ,
,
AC⊥BD,垂足为E.
(Ⅰ)求证BD⊥A1C;
(Ⅱ)求二面角A1—BD—C1的大小;
(Ⅲ)求异面直线AD与BC1所成角的大小.
解法一:
(Ⅰ)在直四棱柱ABCD—A1B1C1D1中,
∵A1A⊥底面ABCD,
∴AC是A1C在平面ABCD上的射影,
∵BD⊥AC, ∴BD⊥A1C.
(Ⅱ)连结A1E,C1E,A1C1.
与(Ⅰ)同理可证BD⊥A1E,BD⊥C1E,
∴∠A1EC1二面角A1—BD—C1的平面角.
∵AD⊥DC, ∴∠A1D1C1=∠ADC=90°,
又A1D1=AD=2,D1C1=DC=2![]() , AA1=
, AA1=![]() ,且AC⊥BD,
,且AC⊥BD,
∴A1C1=4,AE=1,EC=3, ∴A1E=2,C1E=2![]() ,
,
在△A1EC1中,A1C12=A1E2+C1E2, ∴∠A1EC1=90°,
即二面角A1—BD—C1的大小为90°.
(Ⅲ)过B作BF//AD交AC于F,连结FC1,
则∠C1BF就是AD与BC1所成的角.
∵AB=AD=2,BD⊥AC,AE=1, ∴BF=2,EF=1,FC=2,BC=DC,
∴FC1=![]() . 在△BFC1中,
. 在△BFC1中,![]()
∴![]()
即异面直线AD与BC1所成角的大小为![]() .
.
解法二:
(Ⅰ)同解法一.
(Ⅱ)如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.
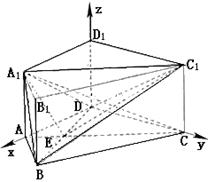 连结A1E,C1F,A1C1.
连结A1E,C1F,A1C1.
与(Ⅰ)同理可证,BD⊥A1E,BD⊥C1E,
∴∠A1EC1为二面角A1—BD—C1的平面角.
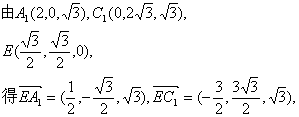

(Ⅲ)如图,由D(0,0,0),A(2,0,0),C1(0,![]() ,
,![]() ,),B(3,
,),B(3,![]() ,0)
,0)
![]()
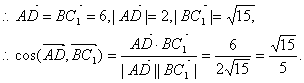
∴异面直线AD与BC1所成角的大小为arccos![]() .
.
 解法三:
解法三:
(I)同解法一.
(II)如图,建立空间直角坐标系,坐标原点为E.
连结A1E,C1E,A1C1.
与(I)同理可证,BD⊥A1E,BD⊥C1E,
∴∠A1EC1为二面角A1—BD—C1的平面角.
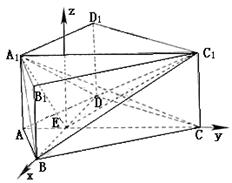
由E(0,0,0),A1(0,-1,![]()
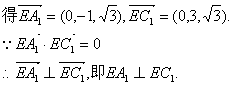
![]() .
.
(Ⅲ)如图,由A(0,-1,0),D(![]() ,0,0),B(
,0,0),B(![]() ,0,0),C1(0,3,
,0,0),C1(0,3,![]() ).
).
得![]() .
.
∵![]()
∴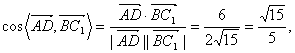
∴异面直线AD与BC1所成角的大小为arccos![]() .
.
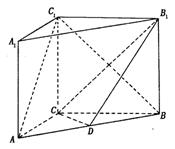 5.(本小题共14分)(2005年高考·北京卷·文16)
5.(本小题共14分)(2005年高考·北京卷·文16)
如图,在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
(Ⅰ)求证AC⊥BC1;
(Ⅱ)求证AC1//平面CDB1;
(Ⅲ)求异面直线AC1与B1C所成角的余弦值.
解法一:
(Ⅰ)∵直三棱柱ABC—A1B1C1底面三边长AC=3,BC=4,AB=5,
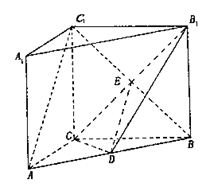 ∴AC⊥BC,且BC1在平面ABC内的射影为BC,
∴AC⊥BC,且BC1在平面ABC内的射影为BC,
∴AC⊥BC1.
(Ⅱ)设CB1与C1B的交点为E,连结DE,
∵D是AB的中点,E是BC1的中点,
∴DE//AC1,
∵DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,
平面CDB1,
∴AC1//平面CDB1.
(Ⅲ)∵DE//AC1,∴∠CED为AC1与B1C所成的角,
在△CED中,ED![]() =
=![]()
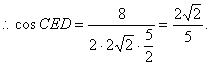
∴异面直线AC1与B1C所成角的余弦值为![]()
解法二:
∵直三棱柱ABC—A1B1C1底面三边长AC=3,BC=4,AB=5,
∴AC,BC,C1C两两垂直.
如图,以C为坐标原点,直线CA,CB,CC1分别为x轴,
y轴,z轴,建立空间直角坐标系,
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),
B1(0,4,4),D(![]() ,2,0).
,2,0).
(Ⅰ)![]()
![]()
(Ⅱ)设CB1与C1B的交点为E,则E(0,2,2).
![]()
![]()
(Ⅲ)![]()
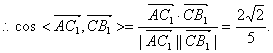
∴异面直线AC1与B1C所成角的余弦值为![]()
 6.(本题满分12分)(2005年高考·上海卷·理17)
6.(本题满分12分)(2005年高考·上海卷·理17)
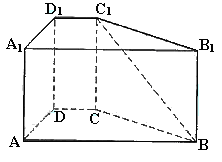
已知直四棱柱![]() 中,
中,![]() ,底面ABCD是直角梯形,∠A是直角,ABCD,AB=4,AD=2,DC=1,求异面直线
,底面ABCD是直角梯形,∠A是直角,ABCD,AB=4,AD=2,DC=1,求异面直线![]() 与DC所成角的大小.(结果用反三角函数值表示)
与DC所成角的大小.(结果用反三角函数值表示)
[解法一]由题意AB//CD,![]() 是异面直线BC1与DC所成的角.
是异面直线BC1与DC所成的角.
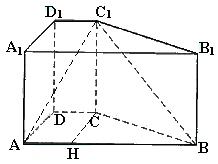 连结AC1与AC,在Rt△ADC中,可得
连结AC1与AC,在Rt△ADC中,可得![]() ,
,
又在Rt△ACC1中,可得AC1=3.
在梯形ABCD中,过C作CH//AD交AB于H,
得![]()
又在![]() 中,可得
中,可得![]() ,
,
在![]()
∴异而直线BC1与DC所成角的大小为![]()
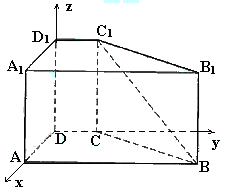 [解法二]如图,以D为坐标原点,分别以AD、DC、DD1所在直线为x、y、z轴建立直
[解法二]如图,以D为坐标原点,分别以AD、DC、DD1所在直线为x、y、z轴建立直
角坐标系.
则C1(0,1,2),B(2,4,0)
![]()
![]() 所成的角为
所成的角为![]() ,
,
则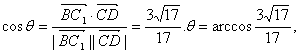
∴异面直线BC1与DC所成角的大小为![]()
7.(本题满分12分)(2005年高考·上海卷·文17)
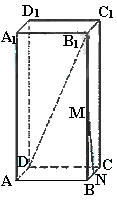 已知长方体
已知长方体![]() 中,M、N分别是
中,M、N分别是![]() 和BC的中点,AB=4,AD=2,
和BC的中点,AB=4,AD=2,![]() 与平面ABCD所成角的大小为
与平面ABCD所成角的大小为![]() ,求异面直线
,求异面直线![]() 与MN所成角的大小.(结果用反三角函数值表示)
与MN所成角的大小.(结果用反三角函数值表示)
[解]联结B1C,由M、N分别是BB1和BC的中点,得B1C//MN
∴∠DB1C就是异面直线B1D与MN所成的角.
联结BD,在Rt△ABD中,可得![]() ,
,
又BB1⊥平面ABCD.
∠B1DB是B1D与平面ABCD的所成的角,
∴∠B1DB=60°.
在Rt△B1BD中,BB1=BDtan60°=![]() ,
,
又DC⊥平面BB1C1C, ∴DC⊥B1C,
在Rt△CB1C中,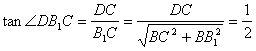
∴∠DB1C=![]()
即异面直线B1D与MN所成角的大小为![]() .
.
8.(本小题满分12分)(2005年高考·福建卷·理20文21)
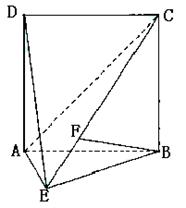 如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
(Ⅲ)求点D到平面ACE的距离.
本小题主要考查直线、直线与平面、二面角及点到平面的距离等基础知识,考查空间想
象能力,逻辑思维能力与运算能力. 满分12分.
解法一:(Ⅰ)![]() 平面ACE.
平面ACE. ![]()
∵二面角D—AB—E为直二面角,且![]() ,
, ![]() 平面ABE.
平面ABE.
![]()
![]()
(Ⅱ)连结BD交AC于C,连结FG,
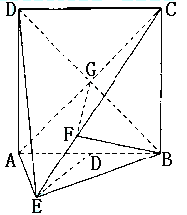 ∵正方形ABCD边长为2,∴BG⊥AC,BG=
∵正方形ABCD边长为2,∴BG⊥AC,BG=![]() ,
,
![]() 平面ACE,
平面ACE,
由三垂线定理的逆定理得FG⊥AC.
![]() 是二面角B—AC—E的平面角.
是二面角B—AC—E的平面角.
由(Ⅰ)AE⊥平面BCE, 又![]() ,
,
∴在等腰直角三角形AEB中,BE=![]() .
.
又![]() 直角
直角![]()
![]() ,
,
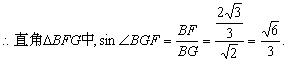
∴二面角B—AC—E等于![]()
(Ⅲ)过点E作![]() 交AB于点O. OE=1.
交AB于点O. OE=1.
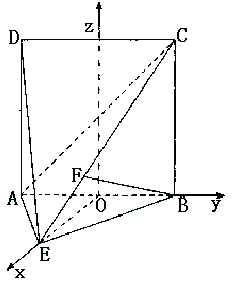 ∵二面角D—AB—E为直二面角,∴EO⊥平面ABCD.
∵二面角D—AB—E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,![]()
![]()
![]() 平面BCE,
平面BCE,![]()
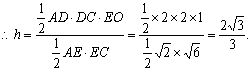
∴点D到平面ACE的距离为![]()
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直
线为x轴,AB所在直线为y轴,过O点平行
于AD的直线为z轴,建立空间直角坐标系
O—xyz,如图.
![]() 面BCE,BE
面BCE,BE![]() 面BCE,
面BCE, ![]() ,
,
在![]() 的中点,
的中点,
![]()
![]() 设平面AEC的一个法向量为
设平面AEC的一个法向量为![]() ,
,
则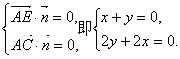
解得![]()
令![]() 得
得![]() 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为![]() ,
,
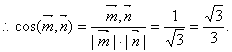
∴二面角B—AC—E的大小为![]()
(III)∵AD//z轴,AD=2,∴![]() ,
,
∴点D到平面ACE的距离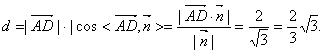
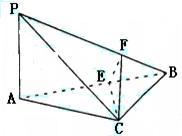 9.(本小题满分14分)(2005年高考·广东卷16)
9.(本小题满分14分)(2005年高考·广东卷16)
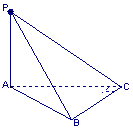
如图3所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=![]() .F是线段PB上一点,
.F是线段PB上一点,![]() ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的大小.
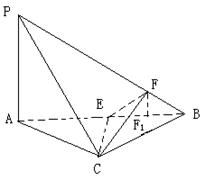 (I)证明:∵
(I)证明:∵![]() ,
,
∴△PAC是以∠PAC为直角的直角三角形.
同理可证:△PAB是以∠PAB为直角的直角三角形,
△PCB是以∠PCB为直角的直角三角形.
所以,PA⊥平面ABC.
又∵![]() ,
,
而![]() ,
,
故CF⊥PB,又已知EF⊥PB,
∴PB⊥平面CEF.
(II)由(I)知PB⊥CE, PA⊥平面ABC,
∴AB是PB在平面ABC上的射影,故AB⊥CE.
在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,
EF1是EF在平面ABC上的射影,∴EF⊥EC,
故∠FEB是二面角B—CE—F的平面角.
![]() ,
,
二面角B—CE—F的大小为![]() .
.
 10.(本小题满分12分)(2005年高考·湖北卷·理20)
10.(本小题满分12分)(2005年高考·湖北卷·理20)
如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=![]() ,BC=1,PA=2,E为PD的中点. (Ⅰ)求直线AC与PB所成角的余弦值;
,BC=1,PA=2,E为PD的中点. (Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.
本小题主要考查线面关系和四棱锥等基础知识,同时考查空间想象能力和推理运算能力.
解法1:(Ⅰ)建立如图所示的空间直角坐标系,
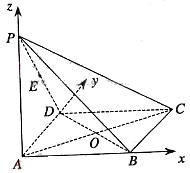 则A、B、C、D、P、E的坐标为A(0,0,0)、
则A、B、C、D、P、E的坐标为A(0,0,0)、
B(![]() ,0,0)、C(
,0,0)、C(![]() ,1,0)、D(0,1,0)、
,1,0)、D(0,1,0)、
P(0,0,2)、E(0,![]() ,1),
,1),
从而![]()
设![]() 的夹角为θ,则
的夹角为θ,则
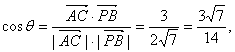
∴AC与PB所成角的余弦值为![]() .
.
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,O,z),则
![]() ,由NE⊥面PAC可得,
,由NE⊥面PAC可得,
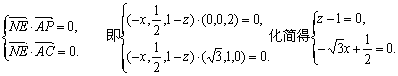 ∴
∴
即N点的坐标为![]() ,从而N点到AB、AP的距离分别为1,
,从而N点到AB、AP的距离分别为1,![]() .
.
解法2:(Ⅰ)设AC∩BD=O,连OE,则OE//PB,
 ∴∠EOA即为AC与PB所成的角或其补角.
∴∠EOA即为AC与PB所成的角或其补角.
在△AOE中,AO=1,OE=![]()
![]()
∴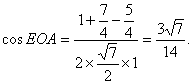
即AC与PB所成角的余弦值为![]() .
.
(Ⅱ)在面ABCD内过D作AC的垂线交AB于F,则![]() .
.
连PF,则在Rt△ADF中![]()
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC,从而NE⊥面PAC.
∴N点到AB的距离![]() ,N点到AP的距离
,N点到AP的距离![]()
11.(本小题满分12分)(2005年高考·湖北卷·文20)
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
(Ⅰ)求BF的长;
(Ⅱ)求点C到平面AEC1F的距离.
 本小题主要考查线面关系和空间距离的求法等基础知识,同时考查空间想象能力和推理运算能力.
本小题主要考查线面关系和空间距离的求法等基础知识,同时考查空间想象能力和推理运算能力.
解法1:(Ⅰ)过E作EH//BC交CC1于H,则CH=BE=1,EH//AD,且EH=AD.
又∵AF∥EC1,∴∠FAD=∠C1EH.
∴Rt△ADF≌Rt△EHC1. ∴DF=C1H=2.
![]()
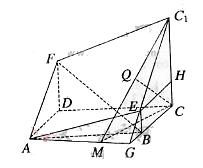
(Ⅱ)延长C1E与CB交于G,连AG,
则平面AEC1F与平面ABCD相交于AG.
过C作CM⊥AG,垂足为M,连C1M,
由三垂线定理可知AG⊥C1M.由于AG⊥面C1MC,且
AG![]() 面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.
面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.
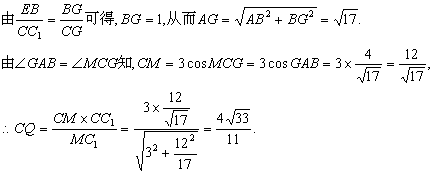
 解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
∵AEC1F为平行四边形,

(II)设![]() 为平面AEC1F的法向量,
为平面AEC1F的法向量,
![]()
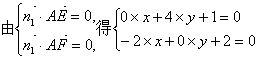
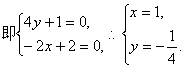
![]() 的夹角为a,则
的夹角为a,则
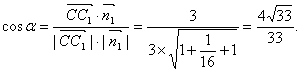
∴C到平面AEC1F的距离为
![]()
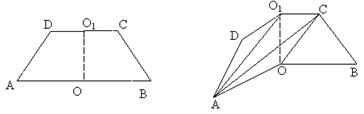 12.(本题满分12分)(2005年高考·湖南卷·理17文18)
12.(本题满分12分)(2005年高考·湖南卷·理17文18)
如图1,已知ABCD是上.下底边长分别为2和6,高为![]() 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
所在直线分别为![]() 轴、y轴、z轴建立空间直角坐标系,
轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1,![]() )
)
|
从而![]()
 所以AC⊥BO1.
所以AC⊥BO1.
(II)解:因为![]() 所以BO1⊥OC,
所以BO1⊥OC,
由(I)AC⊥BO1,所以BO1⊥平面OAC,![]() 是平面OAC的一个法向量.
是平面OAC的一个法向量.
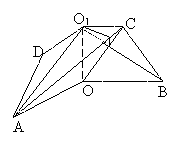 设
设![]() 是0平面O1AC的一个法向量,
是0平面O1AC的一个法向量,
由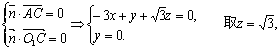 得
得![]() .
.
设二面角O—AC—O1的大小为![]() ,由
,由![]() 、
、![]() 的方向可知
的方向可知![]()
![]() ,
,![]() >,
>,
所以cos![]()
![]() ,
,![]() >=
>=![]()
即二面角O—AC—O1的大小是![]()
解法二(I)证明 由题设知OA⊥OO1,OB⊥OO1,
所以∠AOB是所折成的直二面角的平面角,
|
OC是AC在面OBCO1内的射影.
因为![]()
![]() ,
,
所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1
由三垂线定理得AC⊥BO1.
(II)解 由(I)AC⊥BO1,OC⊥BO1,知BO1⊥平面AOC.
设OC∩O1B=E,过点E作EF⊥AC于F,连结O1F(如图4),则EF是O1F在平面AOC
内的射影,由三垂线定理得O1F⊥AC.
所以∠O1FE是二面角O—AC—O1的平面角.
由题设知OA=3,OO1=![]() ,O1C=1,
,O1C=1,
所以![]() ,
,
从而![]() , 又O1E=OO1·sin30°=
, 又O1E=OO1·sin30°=![]() ,
,
所以![]() 即二面角O—AC—O1的大小是
即二面角O—AC—O1的大小是![]()
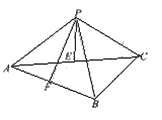 13.(本小题满分12分)(2005年高考·辽宁卷17)
13.(本小题满分12分)(2005年高考·辽宁卷17)
已知三棱锥P—ABC中,E、F分别是AC、AB的中点,
△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P—AB—C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的
球面上,求△ABC的边长.
本小题主要考查空间中的线面关系,三棱锥、球的有关概念及解三角形等基础知识,考
 查空间想象能力及运用方程解未知量的基本方法,满分12分.
查空间想象能力及运用方程解未知量的基本方法,满分12分.
(Ⅰ)证明: 连结CF.
![]()
![]()
![]() ……4分
……4分
(Ⅱ)解法一:![]()
![]() 为所求二面角的平面角. 设AB=a,则AB=a,则
为所求二面角的平面角. 设AB=a,则AB=a,则![]()
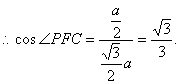 ……………………8分
……………………8分
解法二:设P在平面ABC内的射影为O. ![]() ≌
≌![]() ≌
≌![]()
得PA=PB=PC. 于是O是△ABC的中心. ![]() 为所求二面角的平面角.
为所求二面角的平面角.
设AB=a,则![]()
![]() …………8分
…………8分
(Ⅲ)解法一:设PA=x,球半径为R. ![]()
![]() ,
,![]() 的边长为
的边长为![]() .………12分
.………12分
解法二:延长PO交球面于D,那么PD是球的直径.
连结OA、AD,可知△PAD为直角三角形. 设AB=x,球半径为R.
![]()
![]() .……12分
.……12分
 14.(本小题满分12分)(2005年高考·江西卷·理20文20)如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;
14.(本小题满分12分)(2005年高考·江西卷·理20文20)如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC—D的大小为![]() .
.
解法(一)(1)证明:∵AE⊥平面AA1DD1,A1D⊥AD1,∴A1D⊥D1E
(2)设点E到面ACD1的距离为h,在△ACD1中,AC=CD1=![]() ,AD1=
,AD1=![]() ,
,
故![]()
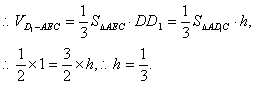
(3)过D作DH⊥CE于H,连D1H、DE,则D1H⊥CE,
∴∠DHD1为二面角D1—EC—D的平面角.
设AE=x,则BE=2-x
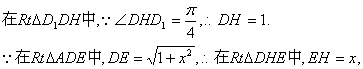

解法(二):以D为坐标原点,直线DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),E(1,x,0),A(1,0,0)C(0,2,0)
(1)![]()
(2)因为E为AB的中点,则E(1,1,0),从而![]() ,
,
![]() ,设平面ACD1的法向量为
,设平面ACD1的法向量为![]() ,则
,则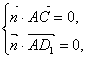
也即![]() ,得
,得![]() ,从而
,从而![]() ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为
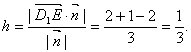
(3)设平面D1EC的法向量![]() ,∴
,∴![]()
由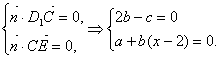 令b=1, ∴c=2,a=2-x,
令b=1, ∴c=2,a=2-x,
∴![]()
依题意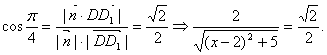
∴![]() (不合,舍去),
(不合,舍去),![]() .
.
∴AE=![]() 时,二面角D1—EC—D的大小为
时,二面角D1—EC—D的大小为![]()
15.(本小题满分13分)(2005年高考·重庆卷·理20)
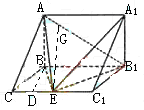
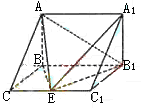 如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=
如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=![]() ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=![]() ,求:
,求:
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
解法一:
(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
又EB1⊥EA,且EA在面BCC1B1内的射影为EB.
由三垂线定理的逆定理知EB1⊥BE,因此BE是异面直线
AB与EB1的公垂线,
在平行四边形BCC1B1中,设EB=x,则EB1=![]() ,
,
作BD⊥CC1,交CC1于D,则BD=BC·![]()
在△BEB1中,由面积关系得![]() .
.
![]() (负根舍去)
(负根舍去)
![]()
解之得CE=2,故此时E与C1重合,由题意舍去![]() .
.
因此x=1,即异面直线AB与EB1的距离为1.
(Ⅱ)过E作EG//B1A1,则GE⊥面BCC1B,故GE⊥EB1且GE在圆A1B1E内,
又已知AE⊥EB1
故∠AEG是二面角A—EB1—A1的平面角.
因EG//B1A1//BA,∠AEG=∠BAE,故![]()
解法二:(Ⅰ)
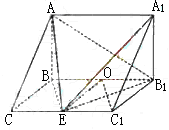
![]()
而BB1C1C得AB⊥EB1从而![]() =0.
=0.

设O是BB1的中点,连接EO及OC1,则在Rt△BEB1中,EO=![]() BB1=OB1=1,
BB1=OB1=1,
因为在△OB1C1中,B1C1=1,∠OB1C1=![]() ,故△OB1C1是正三角形,
,故△OB1C1是正三角形,
所以OC1=OB1=1,
又因∠OC1E=∠B1C1C-∠B1C1O=![]() 故△OC1E是正三角形,
故△OC1E是正三角形,
所以C1E=1,故CE=1,易见△BCE是正三角形,从面BE=1,
即异面直线AB与EB1的距离是1.
(Ⅱ)由(I)可得∠AEB是二面角A—EB1—B的平面角,在Rt△ABE中,由AB=![]() ,
,
BE=1,得tanAEB=![]() .
.
又由已知得平面A1B1E⊥平面BB1C1C,
故二面角A—EB1—A1的平面角![]() ,故
,故
![]()
解法三:
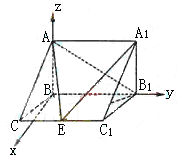 (I)以B为原点,
(I)以B为原点,![]() 、
、![]() 分别为y、z轴建立空间直角坐标系.
分别为y、z轴建立空间直角坐标系.
由于BC=1,BB1=2,AB=![]() ,∠BCC1=
,∠BCC1=![]() ,
,
在三棱柱ABC—A1B1C1中有
B(0,0,0),A(0,0,![]() ),B1(0,2,0),
),B1(0,2,0),
![]()
设![]()
![]()
![]()
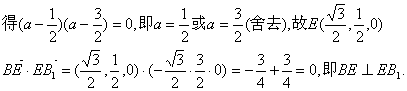
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是异面直线AB、EB1的公垂线,
则![]() ,故异面直线AB、EB1的距离为1.
,故异面直线AB、EB1的距离为1.
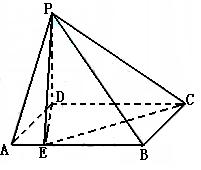
(II)由已知有![]() 故二面角A—EB1—A1的平面角
故二面角A—EB1—A1的平面角![]() 的大小为向量
的大小为向量
![]() 的夹角.
的夹角.
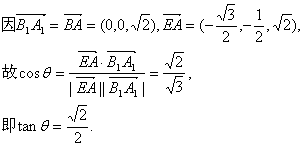
16.(本小题满分13分)(2005年高考·重庆卷·文20)
如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知![]() 求
求
(Ⅰ)异面直线PD与EC的距离;
(Ⅱ)二面角E—PC—D的大小.
解法一:
(Ⅰ)因PD⊥底面,故PD⊥DE,又因EC⊥PE,且DE
是PE在面ABCD内的射影,由三垂直线定理的逆定理知
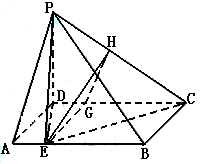 EC⊥DE,因此DE是异面直线PD与EC的公垂线.
EC⊥DE,因此DE是异面直线PD与EC的公垂线.
设DE=x,因△DAE∽△CED,故![]() (负根舍去).
(负根舍去).
从而DE=1,即异面直线PD与EC的距离为1.
(Ⅱ)过E作EG⊥CD交CD于G,作GH⊥PC交PC于H,连接EH. 因PD⊥底面,
故PD⊥EG,从而EG⊥面PCD.
因GH⊥PC,且GH是EH在面PDC内的射影,由三垂线定理知EH⊥PC.
因此∠EHG为二面角的平面角.
在面PDC中,PD=![]() ,CD=2,GC=
,CD=2,GC=![]()
因△PDC∽△GHC,故![]() ,
,
又![]()
故在![]()
![]()
即二面角E—PC—D的大小为![]()
解法二:
 (Ⅰ)以D为原点,
(Ⅰ)以D为原点,![]() 、
、![]() 、
、![]() 分别为x、y、z轴建立空间直角坐标系.
分别为x、y、z轴建立空间直角坐标系.
由已知可得D(0,0,0),P(0,0,![]() ,
,
C(0,2,0)设![]()
![]() 由
由![]() ,
,
即![]() 由
由![]() ,
,
又PD⊥DE,故DE是异面直线PD与CE的公垂线,易得![]() ,故异面直线PD、
,故异面直线PD、
CE的距离为1.
(Ⅱ)作DG⊥PC,可设G(0,y,z).由![]() 得
得![]()
即![]() 作EF⊥PC于F,设F(0,m,n),
作EF⊥PC于F,设F(0,m,n),
则![]()
由![]() ,
,
又由F在PC上得![]()
因![]() 故平面E—PC—D的平面角
故平面E—PC—D的平面角![]() 的大小为向量
的大小为向量![]() 的夹角.
的夹角.
故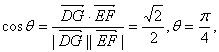 即二面角E—PC—D的大小为
即二面角E—PC—D的大小为![]()
17.(本小题满分14分,第一小问满分6分,第二、第三满分各4分)(2005年高考·江苏卷21)如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=![]() ,∠BAE=∠BCD=∠CDE=1200。
,∠BAE=∠BCD=∠CDE=1200。
(Ⅰ)求异面直线CD与SB所成的角(用反三角函数值表示);
(Ⅱ)证明:BC⊥平面SAB;
(Ⅲ)用反三角函数值表示二面角B-SC-D的大小。(本小问不必写出解答过程)


(21)(Ⅰ)连结BE,延长BC、ED交于点F,
则∠DCF=∠CDF=600,∴△CDF为正三角形,∴CF=DF。
又BC=DE,∴BF=EF。因此,△BFE为正三角形,∴∠FBE=∠FCD=600,∴BE//CD
所以∠SBE(或其补角)就是异面直线CD与SB所成的角。
∵SA⊥底面ABCDE,SA=AB=AE=2,∴SB=![]() ,同理SE=
,同理SE=![]() ,
,
又∠BAE=1200,所以BE=![]() ,从而,cos∠SBE=
,从而,cos∠SBE=![]() ,∴∠SBE=arccos
,∴∠SBE=arccos![]() 。
。
所以异面直线CD与SB所成的角是arccos![]() 。
。
(Ⅱ) 由题意,△ABE为等腰三角形,∠BAE=1200,
∴∠ABE=300,又∠FBE =600,∴∠ABC=900,∴BC⊥BA∵SA⊥底面ABCDE,BC![]() 底面ABCDE,
底面ABCDE,
∴SA⊥BC,又SA![]() BA=A,∴BC⊥平面SAB。
BA=A,∴BC⊥平面SAB。
(Ⅲ)二面角B-SC-D的大小![]() 。
。
18.(2005年高考·浙江卷·理18)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
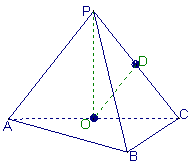 (Ⅰ)当k=
(Ⅰ)当k=![]() 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅱ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
解:方法一:
(Ⅰ) ∵O、D分别为AC、PC中点,![]()
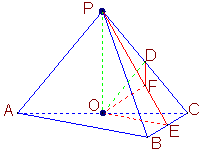
![]() ,
, ![]()
(Ⅱ)![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
又![]() ,
,
![]() PA与平面PBC所成的角的大小等于
PA与平面PBC所成的角的大小等于![]() ,
,
![]()
![]()
(Ⅲ)由(Ⅱ)知,![]() ,∴F是O在平面PBC内的射影
,∴F是O在平面PBC内的射影![]()
∵D是PC的中点,
若点F是![]() 的重心,则B,F,D三点共线,
的重心,则B,F,D三点共线,
∴直线OB在平面PBC内的射影为直线BD,
![]() ,即
,即![]()
![]()
反之,当![]() 时,三棱锥
时,三棱锥![]() 为正三棱锥,
为正三棱锥,
∴O在平面PBC内的射影为![]() 的重心
的重心![]()
方法二:
![]() ,
,![]() ,
,
![]()
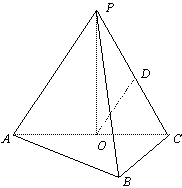
以O为原点,射线OP为非负z轴,建立空间直角坐标系![]() (如图)
(如图)![]()
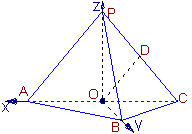 设
设![]() 则
则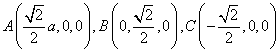 ,
,
设![]() ,则
,则![]()
(Ⅰ)![]() D为PC的中点,
D为PC的中点,
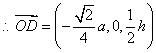 ,
,
又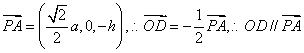 ,
,
![]()
(Ⅱ)![]() ,即
,即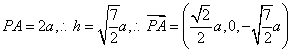 ,
,
可求得平面PBC的法向量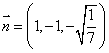 ,
,
![]() ,
,
设PA与平面PBC所成的角为![]() ,则
,则
![]() ,
,
(Ⅲ)![]() 的重心
的重心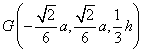 ,
,
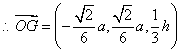 ,
,
![]() ,
,
又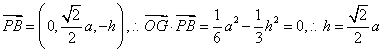 ,
,
![]() ,即
,即![]() ,
,
反之,当![]() 时,三棱锥
时,三棱锥![]() 为正三棱锥,
为正三棱锥,
∴O在平面PBC内的射影为![]() 的重心
的重心![]()
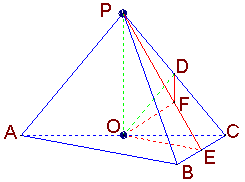
 19.(2005年高考·浙江卷·文18)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=
19.(2005年高考·浙江卷·文18)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=![]() PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证:OD∥平面PAB;
(Ⅱ) 求直线OD与平面PBC所成角的大小.
解:方法一:
(Ⅰ) ∵O、D分别为AC、PC中点,
![]()
![]()
![]()
(Ⅱ)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
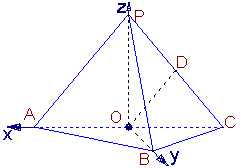
方法二:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
20.(本小题满分12分) (2005年高考·山东卷·理20文20)
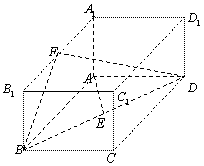 如图,已知长方体
如图,已知长方体![]()
![]()
直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() 垂直
垂直![]() 于
于
![]() ,
,![]() 为
为![]() 的中点.
的中点.
(I)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(II)求平面![]() 与平面
与平面![]() 所成的二面角;
所成的二面角;
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.
解:在长方体![]() 中,以
中,以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴建立如图示空间直角坐标系
轴建立如图示空间直角坐标系
由已知![]() 可得
可得![]() ,
,![]()
又![]() 平面
平面![]() ,从而
,从而![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,又
,又![]() ,
,![]() ,
,![]() 从而易得
从而易得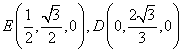
(I)因为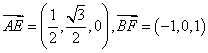 所以
所以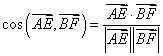 =
=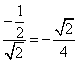
易知异面直线![]() 所成的角为
所成的角为![]()
(II)易知平面![]() 的一个法向量
的一个法向量![]() 设
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() 由
由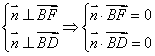
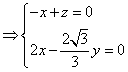
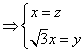
即![]() 所以
所以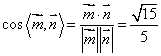 即平面
即平面![]() 与平面
与平面![]() 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为![]()
(III)点![]() 到平面
到平面![]() 的距离,即
的距离,即![]() 在平面
在平面![]() 的法向量
的法向量![]() 上的投影的绝对值,
上的投影的绝对值,
所以距离![]() =
=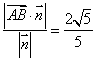 所以点
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]()
21.(本小题满分12分)(2005年高考·天津卷·理19文19)
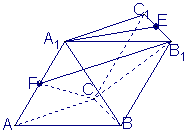 如图,在斜三棱柱
如图,在斜三棱柱![]() 中,
中,![]() ,侧面
,侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点.
的中点.
(Ⅰ)求![]() 与底面ABC所成的角;
与底面ABC所成的角;
(Ⅱ)证明![]() //平面
//平面![]() ;
;
(Ⅲ)求经过![]() 四点的球的体积.
四点的球的体积.
本小题主要考查棱柱、球、二面角、线面关系等基础知识,考查空间想象能力和推理论证能力.满分12分.
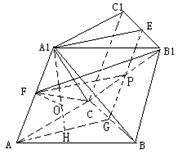 (Ⅰ)解:过A1作A1H⊥平面ABC,垂足为H.
(Ⅰ)解:过A1作A1H⊥平面ABC,垂足为H.
连结AH,并延长交BC于G,连结EG,于是
∠A1AH为A1A与底面ABC所成的角.
∵∠A1AB=∠A1AC, ∴AG为∠BAC的平分线.
又∵AB=AC, ∴AG⊥BC,且G为BC的中点
因此,由三垂线定理,A1A⊥BC.
∵A1A//B1B,且EG//B1B, EG⊥BC 于是
∠AGE为二面角A—BC—E的平面角,即
∠AGE=120°
由于四边形A1AGE为平行四边形,得∠A1AG=60°,
所以,A1A与底面ABC所成的角为60°,
(Ⅱ)证明:设EG与B1C的交点为P,则点P为EG的中点,连结PF.
在平行四边形AGEA1中,因F为A1A的中点,故A1E//FP.
而FP![]() 平面B1FC,A1E//平面B1FC,所以A1E//平面B1FC.
平面B1FC,A1E//平面B1FC,所以A1E//平面B1FC.
(Ⅲ)解:连结A1C,在△A1AC和△A1AB中,由于AC=AB,∠A1AC=∠A1AB,
A1A=A1A,则△A1AC≌△A1AB,故A1C=A1B,由已知得 A1A=A1B=A1C=a.
又∵A1H⊥平面ABC, ∴H为△ABC的外心.
设所求球的球心为O,则O∈A1H,且球心O与A1A中点的连线OF⊥A1A.
在Rt△A1FO中, 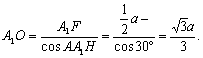
故所求球的半径![]() ,球的体积
,球的体积 ![]()
22.(本小题满分12分)(2005年高考·全国卷Ⅰ·理18文18)
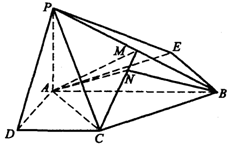
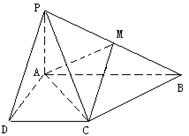 已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DE=
已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DE=![]() AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小.
本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分.
方案一:
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
 ∴由三垂线定理得:CD⊥PD.
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD![]() 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE=![]() ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=![]() ,PB=
,PB=![]() ,
, ![]()
![]()
(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC=![]() ,
,
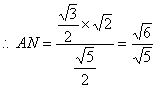 . ∴AB=2,
. ∴AB=2,![]()
故所求的二面角为![]()
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为
A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,![]() .
.
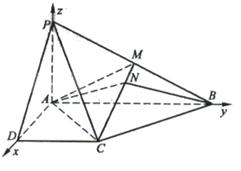
(Ⅰ)证明:因![]()
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
 又DC在面PCD上,故面PAD⊥面PCD.
又DC在面PCD上,故面PAD⊥面PCD.
(Ⅱ)解:因![]()
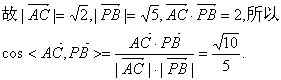
(Ⅲ)解:在MC上取一点N(x,y,z),则存在![]() 使
使![]()
![]()
要使![]()
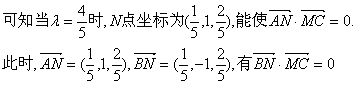
![]() 为所求二面角的平面角.
为所求二面角的平面角.
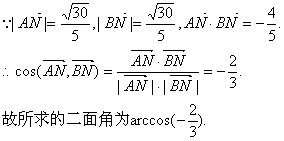
23.(本小题满分12分)(2005年高考·全国卷II·理20文20))
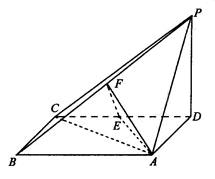 如图,四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.
(Ⅰ)求证:EF⊥平面PAB;
(Ⅱ)设AB=![]() BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.
本小题主要考查直线与平面垂直、直线与平面所成角的有关知识、及思维能力和空间想象能力。满分12分。
证明:(Ⅰ)证明:连结EP, ![]() 底面ABCD,DE在平面ABCD内,
底面ABCD,DE在平面ABCD内,![]() 。
。
又CE=ED,PD=AD=BC,![]()
![]() F为PB中点,∴
F为PB中点,∴![]() 由三垂线定理得
由三垂线定理得![]() ,∴在
,∴在![]() 中,PF=AF。
中,PF=AF。
 又PE=BE=EA,
又PE=BE=EA,
![]()
![]() PB、FA为平面PAB内的相交直线,∴EF
PB、FA为平面PAB内的相交直线,∴EF![]() 平面PAB。
平面PAB。
(Ⅱ)解:不妨设BC=1,则AD=PD=1,AB=![]() ,PA=
,PA=![]() ,AC=
,AC=![]()
∴![]() PAB为等腰直角三角形,且PB=2,F为其斜边中点,BF=1,且AF
PAB为等腰直角三角形,且PB=2,F为其斜边中点,BF=1,且AF![]() PB。
PB。
![]() PB与平面AEF内两条相交直线EF、AF都垂直,∴PB
PB与平面AEF内两条相交直线EF、AF都垂直,∴PB![]() 平面AEF。
平面AEF。
连结BE交AC于G,作GH∥BP交EF于H,则GH![]() 平面AEF,
平面AEF,![]() GAH为AC与平面AEF所成的角。
GAH为AC与平面AEF所成的角。
由![]() EGC∽
EGC∽![]() BGA可知EG=
BGA可知EG=![]() ,
,
由![]() ECH∽
ECH∽![]() EBF可知
EBF可知![]() ,
,
∴![]()
∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
24.(本小题满分12分) (2005年高考·全国卷Ⅲ·理18文19)
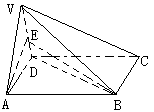
 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(Ⅰ)证明AB⊥平面VAD;
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
证明:方法一:(Ⅰ)证明:
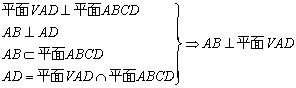
(Ⅱ)解:取VD的中点E,连结AF,BE,
∵△VAD是正三形,
∴AE⊥VD,AE=![]()
∵AB⊥平面VAD, ∴AB⊥AE.
又由三垂线定理知BE⊥VD. 因此,tan∠AEB=![]()
即得所求二面角的大小为![]()
方法二:以D为坐标原点,建立如图所示的坐标图系.
(Ⅰ)证明:不防设作A(1,0,0),
则B(1,1,0), ![]() ,
,
![]()
由![]() 得AB⊥VA. 又AB⊥AD,因而AB与平面VAD内两条相交直线VA,AD都垂直. ∴AB⊥平面VAD.
得AB⊥VA. 又AB⊥AD,因而AB与平面VAD内两条相交直线VA,AD都垂直. ∴AB⊥平面VAD.
(Ⅱ)解:设E为DV中点,则![]() ,
,
![]()
由![]()
因此,∠AEB是所求二面角的平面角,
![]()
解得所求二面角的大小为![]()