试卷类型：A

2003年MAM高考数学仿真试题(七)

MAM:　M-March　A-April　M-May

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

第Ⅰ卷(选择题　共60分)

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.

3.考试结束，监考人将本试卷和答题卡一并收回.

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.集合A={x｜x=(2n+1)π,n∈Z}与集合B={y｜y=(4k±1)π,k∈Z}之间的关系是

A.AB　　　　　　　　　　　　　　　　B.BA　　　　　　　　　　　　 C.A=B　　　　　　　　　　　　 D.A≠B

2.若a=（5，－7），b=（－1，2）且a+λb⊥b，则λ的值为

A.－　　　　　　　　　　　　　　　B.3　　　　　　　　　　　　　　　C. 　　　　　　　　　　　　 D.－3

3.函数y=(0.2)^－x+1的反函数是

A.y=log₅x+1(x＞0)　　　　　　　　　　　　　　　　　　　　　　　　　B.y=log₅(x－1)(x＞1)

C.y=－log₅x－1(x＞0)　　　　　　　　　　　　　　　　　　　　　　 D.y=log₅x－1(x＞0)

4.三门高射炮同时向敌机开火，每门命中的概率分别为，，，则只有一门命中的概率为

A. 　　　　　　　　　　　　　　　 B. 　　　　　　　　　　　　C. 　　　　　　　　　　　　D.

5.a、b∈R⁺则“a＞b”是“a－＞b－”成立的

A.充分不必要条件　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.必要不充分条件

C.充要条件　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.既不充分也不必要条件

6.数列{a_n}是等差数列，S_n是其前n项和且S₅＜S₆,S₆=S₇＞S₈,则下列结论错误的是

A.a₇=0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.d＜0　　　　　　　　　　　　

C.S₉＞S₅ D.S₆与S₇均为S_n的最大值

7.已知A+B+C=0，则直线Ax+By+C=0(A、B、C∈R)被抛物线y²=2x所截得的线段中点M的轨迹方程是

A.y²+y－x+1=0　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.y²－y－x+1=0

C.y²+y+x+1=0　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.y²－y－x－1=0

8.函数y=2sin²x+sin2x是

A.以2π为周期的奇函数

B.以2π为周期的非奇非偶函数

C.以π为周期的奇函数

D.以π为周期的非奇非偶函数

9.若实数x、y满足x²+y²－2x+4y=0则x－2y的最大值为

A. 　　　　　　　　　　　　　　　 B.10　　　　　　　　　　　　　　 C.9　　　　　　　　　　　　　　　D.5+2

10.一个十二面体共8个顶点，其中2个顶点处各有6条棱，其他的顶点处都有相同数目的棱，则其他顶点各有棱的条数为

A.4　　　　　　　　　　　　　　　　　　 B.5　　　　　　　　　　　　　　　C.6　　　　　　　　　　　　　　　D.7

11.用0，1，2，3，4这五个数字组成没有重复数字的四位数，那么，在这些四位数中，是偶数的共有

A.120个　　　　　　　　　　　　　　 B.96个　　　　　　　　　　　　C.60个　　　　　　　　　　　　D.36个

12.已知y=log_a(2－ax)在［0,1］上是x的减函数，则a的取值范围是

A.（0，1）　　　　　　　　　　　　 B.（1，2）　　　　　　　　　C.（0，2）　　　　　　　　　D.［2，+∞］

MAM高考数学仿真试题(七)

第Ⅱ卷(非选择题　共90分)

注意事项：

1.第Ⅱ卷，用钢笔或圆珠笔直接答在试题卷中.

2.答卷前将密封线内的项目填写清楚.

题 号	二	三						总 分
		17	18	19	20	21	22
分 数

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）

13.不等式｜｜＜a(a＞0)的解集为__　　 ___.

14.如果（－）ⁿ的展开式的第八项是含的项，则自然数n的值为__　　 ___.

15.双曲线－y²=1的两个焦点为F₁、F₂，点P在双曲线上，且△PF₁F₂的面积为1，则∠F₁PF₂=____　　 _.

16.将正方形ABCD沿对角线AC折成直二面角后，异面直线AB与CD所成角的大小是_____　　 .

三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）

17.（本小题满分12分）

△ABC中，已知b=1，c=2，且S_△ABC等于以a为边的正三角形的面积，求sin（A+60°）的值.

18.（本小题满分12分）

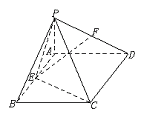如图，已知四棱锥P－ABCD的底面ABCD是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点.

（1）求证：AF∥平面PEC；

（2）若AD=2，CD=2，二面角P－CD－B为45°，求F到平面PEC的距离.

19.（本小题满分12分）

某工厂用平炉（主要使用焦炭，同时必用电）或电炉冶炼合金钢，用平炉冶炼每吨钢的费用为s元，用电炉冶炼每吨钢的费用为p元，若每吨焦炭价为x元，工业用电每万度为y元，则x、y与p、s的关系为：s=5x+2y+50　　p=102y+200.

如果平炉比电炉炼一吨钢的费用低或相同，则用平炉生产，否则用电炉生产.

（1）如果平炉与电炉冶炼费用相同，试将每吨焦炭价格表示为万度电费价的函数；

（2）如果每万度工业用电的价格在60元以上，用平炉生产，那么每吨焦炭的最高限价是多少元？

20.（本小题满分12分）

已知数列{a_n}的相邻两项a_n与a_n+1是方程x²－c_nx+()ⁿ=0的两根，且a₁=2，求数列{c_n}的前2n项之和.

21.（本小题满分12分）

已知常数a＞0，对称轴与坐标轴平行的抛物线C₁与x轴相切于点（－1，0），与直线l:y=2ax相切于点P.

（1）求P点的坐标及C₁的方程；

（2）若抛物线C₂:y=p(x－q)²经过点P，且在P点的切线m与直线l垂直，求p与q的值及m的方程.

22.（本小题满分14分）

已知二次函数f(x)=ax²+bx+c的图象过A（t₁，y₁）、B(t₂,y₂)两点，且满足a²+(y₁+y₂)a+y₁y₂=0.

(1)证明：y₁=－a或y₂=－a；

（2）证明：b²－4ac＞0；

（3）若函数f(x)的图象与x轴的交点为M（x₁,0），N（x₂,0），且x₁＜x₂，证明：x₁＜t₁＜x₂,

x₁＜t₂＜x₂.