试卷类型：A

2003年MAM高考数学仿真试题(六)

MAM:　M-March　A-April　M-May

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

第Ⅰ卷(选择题　共60分)

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.

3.考试结束，监考人将本试卷和答题卡一并收回.

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.不等式（1+x）(1－x)＞0的解集为

A.{x0≤x＜1}　　　　　　　　　　　  　　B.{xx＜0或x≠－1}　

C.{x－1＜x＜1＝　　 　　　　　　　　　　　　D.{xx＜1且x≠－1＝

2.若p为真命题，q为假命题，以下四个命题：

①p且q　②P或q  ③非p  ④非q，其中假命题的个数为

A.1　　　　　　　　　 B.2　　　　  　　　　 C.3　　　　　　　　　D.4

3.已知抛物线x²=4y的焦点F和点A（－1，8），P为抛物线上一点，则PA+PF的最小值是

A.16　　　　 　　　　 B.6　　　　　　　　　 C.12　　　　　　　　　D.9

4.设－＜α＜,－＜β＜，tanα,tanβ是方程x²－3x+4=0的两个不相等的实根，则α+β等于

A.－　　 　　　　　B. 　　　　　　　 C. 　　　　　　　　 D.－

5.有红、黄、蓝三种颜色的小旗各3面，每种颜色的三面小旗上分别标有号码1，2，3，现从中任取3面，它们的颜色和号码都不相同的概率是

A.　　　　　　　　 B.　　　　　　　　 C.　 　　　　　　　 D.

6.某人射8枪，命中4枪，命中的4枪中恰有3枪连在一起的情形的不同种数为

A.720　　 　　　　　　B.480　　　　　　　　 C.224　 　　　　　　　D.20

7.椭圆=1上一点M到焦点F₁的距离为2，N是MF₁的中点，则ON等于

A.2　　　　　　　　　 B.4　　　　　　　　　　C.8　　 　　　　　　 D.

8.如果直线l沿x轴负方向平移3个单位，再沿y轴正方向平移1个单位后，又回到原来的位置，那么直线l的斜率是

A.－　 　　　　　　 B.－3　 　　　　　　　 C. 　　　　　　　　D.3

9.在侧棱长为2，三侧面的顶角为40°的正三棱锥P—ABC中，过A作截面分别交PB，PC于E、F，则△AEF的最小周长是

A.6　　 　　　　　　 B.2　　　 　　　　　C.36　　　　　　　　 D.6

10.若正数a,b,c依次构成公比大于1的等比数列，当x＞1时，log_ax,log_bx,log_cx依次成

A.等差数列　　　　　　　　　　　　　　　　　 B.等比数列　　　　

C.各项倒数成等差数列　　　　　　　　　　　　 D.各项倒数成等比数列

11.实数m,n,x,y满足m²+n²=a,x²+y²=b,那么mx+ny的最大值为

A.　　　　　　　B.　　 　　　　　 C.　　　 　D.

12.用一张钢板制作一个容积为4 m³的无盖长方体水箱，可用的长方形钢板有四种不同的规格（长×宽的尺寸如选项所示，单位为m）.若既要够用，又要所剩最少，则应选择钢板的规格是

A.2×5　 　　　　　　B.2×2.5  　　　　　　　C.2×6.1　 　　　　 D.3×5

第Ⅱ卷(非选择题　共90分)

注意事项：

1.第Ⅱ卷用钢笔或圆珠笔直接答在试题卷中.

2.答卷前将密封线内的项目填写清楚.

题号	二	三						总分
		17	18	19	20	21	22
分数

二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）

13.化简（－）－(－)=________.

14.设y=f(x)是二次函数，方程f(x)=0有两个相等实根且f '(x)=2x+2,则y=f(x)的表达式是________.

15.已知函数f(x)=log₃x+2,x∈［1,9］,则函数y=［f(x)］²+f(x²)的值域是________.

16.对于定义在R上的函数f(x),若实数x₀满足f(x₀)=x₀,则称x₀是函数f(x)的一个不动点，现给定一个实数a∈(4,5),则函数f(x)=x²+ax+1的不动点共有________个.

三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）

17.（本小题满分12分）

已知函数f(x)=Asinωx+Bcosωx(其中A，B，ω为实常数，且ω＞0）的最小正周期为2，并且当x=时，f(x)的最大值为2.

（1）求函数f(x)的表达式；

（2）在区间［］上函数f(x)存在对称轴，求此对称轴方程.

18.（本小题满分12分）

已知数列{a_n}为等差数列，{b_n}为等比数列，且b₁=a₁²,b₂=a₂²,b₃=a₃²(a₁＜a₂),q为等比数列的公比，又q＜1.求:

(1)等比数列的公比q;

(2)又若a₁=－时，等差数列的前10项和为多少？

19.（本小题满分12分）

设有两门高射炮，每一门击中飞机的概率为0.6，用这两门炮同时发射一发炮弹击中飞机的概率为多少？又若有一架敌机入侵领空，欲以99%以上的概率击中它，问至少需要多少门这样的高射炮？

2０.（本小题满分12分）

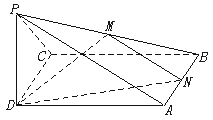
如图，已知正四棱锥P—ABCD的底面为边长是a的正方形，PD⊥底面ABCD，设PD=6，M，N分别为PB，AB的中点.求：

（1）三棱锥P—DMN的体积；

（2）二面角M—DN—C的平面角的正切值.

21.（本小题满分12分）

已知函数f(x)=－x³+ax²+bx在区间（－2，1）内，当x=－1时取得极小值，x=时取得极大值.求：

（1）函数y=f(x)在x=－2时的对应点的切线方程；

（2）函数f(x)在［－2，1］上的最大值与最小值.

22.（本小题满分14分）

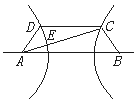如图，已知梯形ABCD中，AB=2CD，点E满足=λ,双曲线过C、D、E三点，且以A、B为焦点，当≤λ≤时，求双曲线离心率e的取值范围.