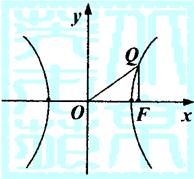
1.椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]() (
(![]() )的准线
)的准线![]() 与x轴相交于点
与x轴相交于点![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 、
、![]() 两点。
两点。
(1)求椭圆的方程及离心率;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设![]() (
(![]() ),过点
),过点![]() 且平行于准线
且平行于准线![]() 的直线与椭圆相交于另一点
的直线与椭圆相交于另一点![]() ,证明
,证明![]() . (14分)
. (14分)
2.
已知函数![]() 对任意实数x都有
对任意实数x都有![]() ,且当
,且当![]() 时,
时,![]() 。
。
(1) ![]() 时,求
时,求![]() 的表达式。
的表达式。
(2) 证明![]() 是偶函数。
是偶函数。
(3) 试问方程![]() 是否有实数根?若有实数根,指出实数根的个数;若没有实数根,请说明理由。当
是否有实数根?若有实数根,指出实数根的个数;若没有实数根,请说明理由。当
3.(本题满分12分)如图,已知点F(0,1),直线L:y=-2,及圆C:![]() 。
。
(1) 若动点M到点F的距离比它到直线L的距离小1,求动点M的轨迹E的方程;
(2) 过点F的直线g交轨迹E于G(x1,y1)、H(x2,y2)两点,求证:x1x2 为定值;
(3) 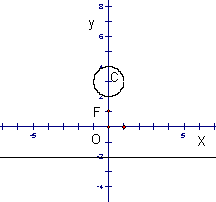 过轨迹E上一点P作圆C的切线,切点为A、B,要使四边形PACB的面积S最小,求点P的坐标及S的最小值。
过轨迹E上一点P作圆C的切线,切点为A、B,要使四边形PACB的面积S最小,求点P的坐标及S的最小值。
4.以椭圆![]() =1(a>1)短轴一端点为直角顶点,作椭圆内接等腰直角三角形,试判断并推证能作出多少个符合条件的三角形.
=1(a>1)短轴一端点为直角顶点,作椭圆内接等腰直角三角形,试判断并推证能作出多少个符合条件的三角形.
5 已知,二次函数f(x)=ax2+bx+c及一次函数g(x)=-bx,其中a、b、c∈R,a>b>c,a+b+c=0.
(Ⅰ)求证:f(x)及g(x)两函数图象相交于相异两点;
(Ⅱ)设f(x)、g(x)两图象交于A、B两点,当AB线段在x轴上射影为A1B1时,试求A1B1的取值范围.
6
已知过函数f(x)=![]() 的图象上一点B(1,b)的切线的斜率为-3。
的图象上一点B(1,b)的切线的斜率为-3。
(1) 求a、b的值;
(2) 求A的取值范围,使不等式f(x)≤A-1987对于x∈[-1,4]恒成立;
(3)
令![]() 。是否存在一个实数t,使得当
。是否存在一个实数t,使得当![]() 时,g(x)有最大值1?
时,g(x)有最大值1?
7
已知两点M(-2,0),N(2,0),动点P在y轴上的射影为H,︱![]() ︱是2和
︱是2和![]() 的等比中项。
的等比中项。
(1) 求动点P的轨迹方程,并指出方程所表示的曲线;
(2) 若以点M、N为焦点的双曲线C过直线x+y=1上的点Q,求实轴最长的双曲线C的方程。
8.已知数列{an}满足![]()
(1)求数列{bn}的通项公式;
(2)设数列{bn}的前项和为Sn,试比较Sn与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
9.已知焦点在![]() 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线![]() 对称.
对称.
(Ⅰ)求双曲线C的方程;
(Ⅱ)设直线![]() 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线![]() 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线![]() 在
在![]() 轴上的截距b的取值范围;
轴上的截距b的取值范围;
(Ⅲ)若Q是双曲线C上的任一点,![]() 为双曲线C的左,右两个焦点,从
为双曲线C的左,右两个焦点,从![]() 引
引![]() 的平分线的垂线,垂足为N,试求点N的轨迹方程.
的平分线的垂线,垂足为N,试求点N的轨迹方程.
10. ![]() 对任意
对任意![]() 都有
都有![]()
(Ⅰ)求![]() 和
和![]() 的值.
的值.
(Ⅱ)数列![]() 满足:
满足:![]() =
=![]() +
+![]() ,数列
,数列![]() 是等差数列吗?请给予证明;
是等差数列吗?请给予证明;
 (Ⅲ)令
(Ⅲ)令![]()
试比较![]() 与
与![]() 的大小.
的大小.
11. :如图,设OA、OB是过抛物线y2=2px顶点O的两条弦,且=0,求以OA、OB为直径的两圆的另一个交点P的轨迹.(13分)
12.知函数f(x)=log3(x2-2mx+2m2+)的定义域为R
(1)求实数m的取值集合M;
(2)求证:对m∈M所确定的所有函数f(x)中,其函数值最小的一个是2,并求使函数值等于2的m的值和x的值.
13.设关于x的方程2x2-tx-2=0的两根为![]() 函数f(x)=
函数f(x)=![]()
(1). 求f(![]() 的值。
的值。
(2)。证明:f(x)在[![]() 上是增函数。
上是增函数。
(3)。对任意正数x1、x2,求证:![]()
14.已知数列{an}各项均为正数,Sn为其前n项的和.对于任意的![]() ,都有
,都有![]() .
.
I、求数列![]() 的通项公式.
的通项公式.
II、若![]() 对于任意的
对于任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
15.(
12分)已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足![]() ·
·![]() =0,
=0,![]() =-
=-![]()
![]() ,
,
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-1,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使得△ABE为等边三角形,求x0的值.
16.(14分)设f1(x)=![]() ,定义fn+1 (x)=f1[fn(x)],an=
,定义fn+1 (x)=f1[fn(x)],an=![]() ,其中n∈N*.
,其中n∈N*.
(1) 求数列{an}的通项公式;
(2)若T2n=a1+2a2+3a3+…+2na2n,Qn=![]() ,其中n∈N*,试比较9T2n与Qn的大小.
,其中n∈N*,试比较9T2n与Qn的大小.
17. 已知![]() =(x,0),
=(x,0),![]() =(1,y),(
=(1,y),(![]() +
+![]()
![]() )
)![]() (
(![]() –
–![]()
![]() ).
).
(I)
求点![]() (x,y)的轨迹C的方程;
(x,y)的轨迹C的方程;
(II)
若直线L:y=kx+m(m![]() 0)与曲线C交于A、B两点,D(0,–1),且有 AD=BD,试求m的取值范围.
0)与曲线C交于A、B两点,D(0,–1),且有 AD=BD,试求m的取值范围.
18.已知函数![]() 对任意实数p、q都满足
对任意实数p、q都满足![]()
![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)设![]() 求证:
求证:![]()
(3)设![]() 试比较
试比较![]() 与6的大小.
与6的大小.
19.已知函数![]() 若数列:
若数列:![]() …,
…,
![]() 成等差数列.
成等差数列.
(1)求数列![]() 的通项
的通项![]() ;
;
(2)若![]() 的前n项和为Sn,求
的前n项和为Sn,求![]() ;
;
(3)若![]() ,对任意
,对任意![]() ,求实数t的取值范围.
,求实数t的取值范围.
20.已知△OFQ的面积为![]()
(1)设![]() 正切值的取值范围;
正切值的取值范围;
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),![]() ,
,
当![]() 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.
(3)设F1为(2)中所求双曲线的左焦点,若A、B分别为此双曲线渐近线l1、l2上的动
|
21、已知函数![]() 是偶函数,
是偶函数,![]() 是奇函数,正数数列
是奇函数,正数数列![]() 满足
满足![]()
①
求![]() 的通项公式;
的通项公式;
②若![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() .
.
22、直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=![]() ,BC=
,BC=![]() .椭圆C以A、B为焦点且经过点D.
.椭圆C以A、B为焦点且经过点D.
(1)建立适当坐标系,求椭圆C的方程;
(2)若点E满足![]()
![]()
![]() ,问是否存在不平行AB的直线l与椭圆C交于M、N两点且
,问是否存在不平行AB的直线l与椭圆C交于M、N两点且![]() ,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
,若存在,求出直线l与AB夹角的范围,若不存在,说明理由.
23、.设函数![]()
(1)求证:对一切![]() 为定值;
为定值;
(2)记![]() 求数列
求数列![]() 的通项公式及前n项和.
的通项公式及前n项和.
24. 已知函数![]() 是定义在R上的偶函数.当X
是定义在R上的偶函数.当X![]() 0时,
0时, ![]() =
=![]() .
.
(I)
求当X<0时, ![]() 的解析式;
的解析式;
(II)
试确定函数![]() =
=![]() (X
(X![]() 0)在
0)在![]() 的单调性,并证明你的结论.
的单调性,并证明你的结论.
(III)
若![]() 且
且![]() ,证明:
,证明:![]() -
-![]() <2.
<2.
25、已知抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() 点,过
点,过![]() 作直线与抛物线交于A、B两点,若线段AB的垂直平分线与X轴交于D(X0,0)
作直线与抛物线交于A、B两点,若线段AB的垂直平分线与X轴交于D(X0,0)
⑴求X0的取值范围。
⑵△ABD能否是正三角形?若能求出X0的值,若不能,说明理由。
26、已知□ABCD,A(-2,0),B(2,0),且∣AD∣=2
⑴求□ABCD对角线交点E的轨迹方程。
⑵过A作直线交以A、B为焦点的椭圆于M、N两点,且∣MN∣=![]() ,MN的中点到Y轴的距离为
,MN的中点到Y轴的距离为![]() ,求椭圆的方程。
,求椭圆的方程。
⑶与E点轨迹相切的直线l交椭圆于P、Q两点,求∣PQ∣的最大值及此时l的方程。
 |
27.(14分)(理)已知椭圆![]() ,直线l过点A(-a,0)和点B(a,ta)
,直线l过点A(-a,0)和点B(a,ta)
(t>0)交椭圆于M.直线MO交椭圆于N.(1)用a,t表示△AMN的面积S;
 (2)若t∈[1,2],a为定值,求S的最大值.
(2)若t∈[1,2],a为定值,求S的最大值.
28.已知函数f(x)= 的图象过原点,且关于点(-1,1)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}(n∈N*)满足:an>0,a1=1,an+1= [f()]2,求数列{an}的通项公式an,并证明你的结论.
30、已知点集![]() 其中
其中![]() 点列
点列![]() 在
在![]() 中,
中,![]() 为
为![]() 与
与![]() 轴的交点,等差数列
轴的交点,等差数列![]() 的公差为1,
的公差为1,![]() 。
。
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() 求
求![]() ;
;
(3)若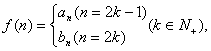 是否存在
是否存在![]() 使得
使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
21.经过抛物线![]() 的焦点F的直线
的焦点F的直线![]() 与该抛物线交于
与该抛物线交于![]() 、
、![]() 两点. (12分)
两点. (12分)
(1)若线段![]() 的中点为
的中点为![]() ,直线的斜率为
,直线的斜率为![]() ,试求点
,试求点![]() 的坐标,并求点
的坐标,并求点![]() 的轨迹方程
的轨迹方程
(2)若直线![]() 的斜率
的斜率![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
1(1)解:由题意,可设椭圆的方程为![]() 。
。
由已知得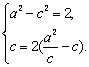 解得
解得![]()
所以椭圆的方程为![]() ,离心率
,离心率![]() 。
。
(2)解:由(1)可得A(3,0)。
设直线PQ的方程为![]() 。由方程组
。由方程组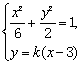
得![]() ,依题意
,依题意![]() ,得
,得![]() 。
。
设![]() ,则
,则![]() , ①
, ① ![]() 。 ②
。 ②
由直线PQ的方程得![]() 。于是
。于是
![]() 。 ③
。 ③
∵![]() ,∴
,∴![]() 。 ④
。 ④
由①②③④得![]() ,从而
,从而![]() 。
。
所以直线PQ的方程为![]() 或
或![]()
(3,理工类考生做)证明:![]() 。由已知得方程组
。由已知得方程组

注意![]() ,解得
,解得![]()
因![]() ,故
,故
![]()
![]() 。
。
而![]() ,所以
,所以![]() 。
。
2 ①f(x)=![]() (2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1,4]上有4个实根
(2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1,4]上有4个实根
3 ①x2=4y ②x1x2=-4 ⑶P(±2,1) SMIN=![]()
4 .解:因a>1,不防设短轴一端点为B(0,1)
设BC∶y=kx+1(k>0)
则AB∶y=-![]() x+1
x+1
把BC方程代入椭圆,
是(1+a2k2)x2+2a2kx=0
∴BC=![]() ,同理AB=
,同理AB=![]()
由AB=BC,得k3-a2k2+ka2-1=0
(k-1)[k2+(1-a2)k+1]=0
∴k=1或k2+(1-a2)k+1=0
当k2+(1-a2)k+1=0时,Δ=(a2-1)2-4
由Δ<0,得1<a<![]()
由Δ=0,得a=![]() ,此时,k=1
,此时,k=1
故,由Δ≤0,即1<a≤![]() 时有一解
时有一解
由Δ>0即a>![]() 时有三解
时有三解
5 解:依题意,知a、b≠0
∵a>b>c且a+b+c=0
∴a>0且c<0
(Ⅰ)令f(x)=g(x),
得ax2+2bx+c=0.(*)
Δ=4(b2-ac)
∵a>0,c<0,∴ac<0,∴Δ>0
∴f(x)、g(x)相交于相异两点
(Ⅱ)设x1、x2为交点A、B之横坐标
则A1B12=x1-x22,由方程(*),知
A1B12=![]()
![]()
![]()
∵![]() ,而a>0,∴
,而a>0,∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∴4[(![]() )2+
)2+![]() +1]∈(3,12)
+1]∈(3,12)
∴A1B1∈(![]() ,2
,2![]() )
)
6、解:(1)![]() =
=![]()
依题意得k=![]() =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3
![]() ,把B(1,b)代入得b=
,把B(1,b)代入得b=![]()
∴a=-3,b=-1
(2)令![]() =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987
∴A≥2004。
(1)
已知g(x)=-![]()
∴![]()
∵0<x≤1,∴-3≤-3x2<0,
①
当t>3时,t-3x2>0,![]()
∴g(x)在![]() 上为增函数,
上为增函数,
g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)
②
当0≤t≤3时, ![]()
令![]() =0,得x=
=0,得x=![]()
列表如下:
| x | (0, |
|
|
|
| + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
g(x)在x=![]() 处取最大值-
处取最大值-![]() +t
+t![]() =1
=1
∴t=![]() =
=![]() <
<![]() 3
3
∴x=![]() <1
<1
③当t<0时,![]() <0,∴g(x)在
<0,∴g(x)在![]() 上为减函数,
上为减函数,
∴g(x)在![]() 上为增函数,
上为增函数,
∴存在一个a=![]() ,使g(x)在
,使g(x)在![]() 上有最大值1。
上有最大值1。
7、解:(1)设动点的坐标为P(x,y),则H(0,y),![]() ,
,![]() =(-2-x,-y)
=(-2-x,-y)
![]() =(2-x,-y)
=(2-x,-y)
∴![]() ·
·![]() =(-2-x,-y)·(2-x,-y)=
=(-2-x,-y)·(2-x,-y)=![]()
![]()
由题意得∣PH∣2=2·![]() ·
·![]()
即![]()
即![]() ,所求点P的轨迹为椭圆
,所求点P的轨迹为椭圆
(2)由已知求得N(2,0)关于直线x+y=1的对称点E(1,-1),则∣QE∣=∣QN∣
双曲线的C实轴长2a=![]() (当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为
(当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为![]()
所以,双曲线C的实半轴长a=![]()
又![]()
∴双曲线C的方程式为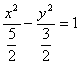
8.(1)![]()
(2)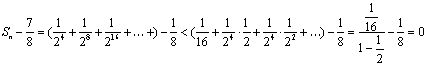
9.解:(Ⅰ)设双曲线C的渐近线方程为y=kx,则kx-y=0
∵该直线与圆![]() 相切,
相切,
∴双曲线C的两条渐近线方程为y=±x.…………………………………………2分
故设双曲线C的方程为![]() .
.
又双曲线C的一个焦点为 ![]()
∴![]() ,
,![]() .
.
∴双曲线C的方程为![]() .………………………………………………4分
.………………………………………………4分
(Ⅱ)由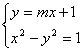 得
得![]() .
.
令![]()
直线与双曲线左支交于两点,等价于方程f(x)=0在![]() 上有两个不等实根.
上有两个不等实根.
因此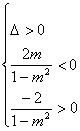 解得
解得![]() .
.
又AB中点为![]() ,
,
∴直线l的方程为![]() .………………………………6分
.………………………………6分
令x=0,得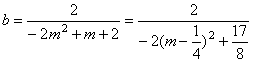 .
.
∵![]() ,
,
∴![]()
∴![]() .………………………………………………8分
.………………………………………………8分
(Ⅲ)若Q在双曲线的右支上,则延长![]() 到T,使
到T,使![]() ,
,
若Q在双曲线的左支上,则在![]() 上取一点T,使
上取一点T,使![]() .
.
根据双曲线的定义![]() ,所以点T在以
,所以点T在以![]() 为圆心,2为半径的圆上,即点T的轨迹方程是
为圆心,2为半径的圆上,即点T的轨迹方程是
![]() ①…………………………………………10分
①…………………………………………10分
由于点N是线段![]() 的中点,设
的中点,设![]() ,
,![]() .
.
则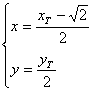 ,即
,即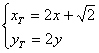 .
.
代入①并整理得点N的轨迹方程为![]() .
.![]() ………………12分
………………12分
10 解:(Ⅰ)因为![]() .所以
.所以![]() .……2分
.……2分
令![]() ,得
,得![]() ,即
,即![]() .……………4分
.……………4分
(Ⅱ)![]()
又![]() ………………5分
………………5分
两式相加
![]() .
.
所以![]() ,………………7分
,………………7分
又![]() .故数列
.故数列![]() 是等差数列.………………9分
是等差数列.………………9分
(Ⅲ)![]()
![]()
![]()
![]() ………………10分
………………10分
![]() ………………12分
………………12分
![]()
所以![]() ……………………………………………………………………14分
……………………………………………………………………14分
11.设直线OA的斜率为k,显然k存在且不等于0
则OA的方程为y=kx
由解得A() ……4分
又由,知OA⊥OB,所以OB的方程为y=-x
由解得B(2pk2,-2pk) ……4分
从而OA的中点为A'(),OB的中点为B'(pk2,-pk) ……6分
所以,以OA、OB为直径的圆的方程分别为
x2+y2-=0
……①
x2+y2-2pk2x+2pky=0
……② ……10分
∵P(x,y)是异于O点的两圆交点,所以x≠0,y≠0
由①-②并化简得y=(k-)x
……③
将③代入①,并化简得x(k2+-1)=2p ……④
由③④消去k,有x2+y2-2px=0
∴点P的轨迹为以(p,0)为圆心,p为半径的圆(除去原点). ……13分
12.(1)由题意,有x2-2mx+2m2+>0对任意的x∈R恒成立
所以△=4m2-4(2m2+)<0
即-m2-<0
∴>0
由于分子恒大于0,只需m2-3>0即可
所以m<-或m>
∴M={mm<-或m>} ……4分
(2)x2-2mx+2m2+=(x-m)2+m2+≥m2+
当且仅当x=m时等号成立.
所以,题设对数函数的真数的最小值为m2+ ……7分
又因为以3为底的对数函数为增函数
∴f(x)≥log3(m2+)
∴当且仅当x=m(m∈M)时,f(x)有最小值为log3(m2+) ……10分
又当m∈M时,m2-3>0
∴m2+=m2-3++3≥2+3=9
当且仅当m2-3=,即m=±时,
log3(m2+)有最小值log3(6+)=log39=2
∴当x=m=±时,其函数有最小值2.
13.解析:(1)。,由根与系数的关系得,![]()
![]()
同法得f(![]()
(2).证明:![]() f/(x)=
f/(x)=![]() 而当x
而当x![]() 时,
时,
2x2-tx-2=2(x-![]() 故当x
故当x![]() 时, f/(x)≥0,
时, f/(x)≥0,
![]() 函数f(x)在[
函数f(x)在[![]() 上是增函数。
上是增函数。
(3)。证明:![]()
![]() , 同理
, 同理![]() .
.
![]()
又f(![]() 两式相加得:
两式相加得:
![]()
即![]()
而由(1),f(![]() 且f(
且f(![]() ,
,
![]()
![]() .
.
14(I)![]() 当
当![]() 时,
时,![]() ,
,
![]() ,又{an}各项均为正数,
,又{an}各项均为正数,![]() .数列
.数列![]() 是等差数列,
是等差数列, ![]()
(II) ![]() ,若
,若![]() 对于任意的
对于任意的![]() 恒成立,则
恒成立,则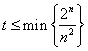 .令
.令![]() ,.当
,.当![]() 时,
时,![]() .又
.又![]() ,
,![]()
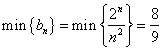 .
.![]()
![]() 的最大值是
的最大值是![]() .
.
15.(1)设点M的坐标为(x,y),由![]() =-
=-![]()
![]() ,得P(0,-
,得P(0,-![]() ),Q(
),Q(![]() ,0), 2分
,0), 2分
由![]() ·
·![]() =0,得(3,-
=0,得(3,-![]() )(x,
)(x,![]() )=0,又得y2=4x, 5分
)=0,又得y2=4x, 5分
由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点. 6分
(2)设直线l:y=k(x+1),其中k≠0,代入y2=4x,得k2x2+2(k2-2)x+k2=0,① 7分
设A(x1,y1),B(x2,y2),
则x1,x2是方程①的两个实根,∴x1+x2=-![]() ,x1x2=1,
,x1x2=1,
所以,线段AB的中点坐标为(![]() ,
,![]() ), 8分
), 8分
线段AB的垂直平分线方程为y-![]() =-
=-![]() (x-
(x-![]() ), 9分
), 9分
令y=0,x0=![]() +1,所以点E的坐标为(
+1,所以点E的坐标为(![]() +1,0)
+1,0)
因为△ABE为正三角形,所以点E(![]() +1,0)到直线AB的距离等于
+1,0)到直线AB的距离等于![]() |AB|,
|AB|,
而|AB|=![]() =
=![]() ·
·![]() , 10分
, 10分
所以,![]() =
=![]() , 11分
, 11分
解得k=±![]() ,得x0=
,得x0=![]() . 12分
. 12分
16.(1)f1(0)=2,a1=![]() =
=![]() ,fn+1(0)=f1[fn(0)]=
,fn+1(0)=f1[fn(0)]=![]() ,
,
an+1=![]() =
=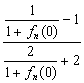 =
=![]() =-
=-![]()
![]() =-
=-![]() an, 4分
an, 4分
∴数列{an}是首项为![]() ,公比为-
,公比为-![]() 的等比数列,∴an=
的等比数列,∴an=![]() (-
(-![]() )n-1. 6分
)n-1. 6分
(2)T2n=a1+2a2+3a3+…+(2n-1)a2n-1+2na2n,
-![]() T2n=(-
T2n=(-![]() a1)+(-
a1)+(-![]() )2a2+(-
)2a2+(-![]() )3a3+…+(-
)3a3+…+(-![]() )(2n-1)a2n-1+(-
)(2n-1)a2n-1+(-![]() )·2na2n
)·2na2n
=a2+2a3+…+(2n-1)a2n-na2n, 8分
两式相减得![]() T2n=a1+a2+a3+…+a2n+na2n,
T2n=a1+a2+a3+…+a2n+na2n,
所以,![]() T2n=
T2n=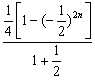 +n×
+n×![]() (-
(-![]() )2n-1=
)2n-1=![]() -
-![]() (-
(-![]() )2n+
)2n+![]() (-
(-![]() )2n-1, 10分
)2n-1, 10分
T2n=![]() -
-![]() (-
(-![]() )2n+
)2n+![]() (-
(-![]() )2n-1=
)2n-1=![]() (1-
(1-![]() ).
∴9T2n=1-
).
∴9T2n=1-![]() ,
,
Qn=1-![]() , 12分
, 12分
当n=1时,22n=4,(2n+1)2=9,∴9T2n<Qn;
当n=2时,22n=16,(2n+1)2=25,∴9T2n<Qn; 13分
当n≥3时,22n=[(1+1)n]2
=(C![]() +C
+C![]() +C
+C![]() +…+C
+…+C![]() )2>(2n+1)2,∴9T2n>Qn. 14分
)2>(2n+1)2,∴9T2n>Qn. 14分
17.解(I)![]() +
+![]()
![]() =(x,0)+
=(x,0)+![]() (1,y)=(x+
(1,y)=(x+![]() ,
,![]() y),
y),
![]() –
–![]()
![]() =(x, 0)
=(x, 0)![]()
![]() (1,y)= (x
(1,y)= (x![]()
![]() ,–
,–![]() y).
y).![]() (
(![]() +
+![]()
![]() )
)![]() (
(![]()
![]()
![]()
![]() ),
),
![]() (
(![]() +
+![]()
![]() )·(
)·(![]()
![]()
![]()
![]() )=0,
)=0, ![]() (x+
(x+![]() )( x
)( x![]()
![]() )+
)+![]() y·(
y·(![]()
![]() y)=0,
y)=0,
故P点的轨迹方程为![]() . (6分)
. (6分)
(II)考虑方程组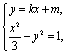 消去y,得(1–3k2)x2-6kmx-3m2-3=0
(*)
消去y,得(1–3k2)x2-6kmx-3m2-3=0
(*)
显然1-3k2![]() 0,
0, ![]() =(6km)2-4(1-3k2)( -3m2-3)=12(m2+1-3k2)>0.
=(6km)2-4(1-3k2)( -3m2-3)=12(m2+1-3k2)>0.
设x1,x2为方程*的两根,则x1+x2=![]() ,x0=
,x0=![]() , y0=kx0+m=
, y0=kx0+m=![]() ,
,
故AB中点M的坐标为(![]() ,
,![]() ),
),
![]() 线段AB的垂直平分线方程为y
线段AB的垂直平分线方程为y![]()
![]() =(
=(![]()
![]() )
)![]() ,
,
将D(0,–1)坐标代入,化简得 4m=3k2![]() 1,
1,
故m、k满足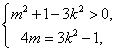 消去k2得 m2
消去k2得 m2![]() 4m>0, 解得 m<0或m>4.
4m>0, 解得 m<0或m>4.
又![]() 4m=3k2
4m=3k2![]() 1>
1>![]() 1,
1, ![]()
![]() 故m
故m![]() (
(![]()
![]() ,0)
,0)![]() (4,+
(4,+![]() ). (12分)
). (12分)
18.(1)解 由已知得![]()
![]() . (4分)
. (4分)
(2)证明 由(1)可 知 ![]() 设
设![]()
![]()
则![]()
![]() .
.
两式相减得![]() +…+
+…+![]()
![]()
![]()
![]() . (9分)
. (9分)
(3)解 由(1)可知![]()
则![]() =
=![]()
故有![]()
![]() =6
=6![]() . (14分)
. (14分)
19.(1)![]()
(2)![]()
(3)![]()
![]()
![]() 为递增数列
为递增数列 ![]() 中最小项为
中最小项为![]()
20.(1)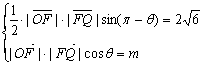
![]()
![]()
![]()
(2)设所求的双曲线方程为![]()
![]() 又由
又由![]()
![]()
当且仅当c=4时,![]() 最小,此时Q的坐标为
最小,此时Q的坐标为![]()
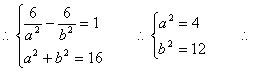 所求方程为
所求方程为![]()
(3)设![]()
![]() 的方程为
的方程为![]() 的方程为
的方程为![]() 则有
则有![]() ①
①
![]() ②
② ![]()
![]()
![]() ③ 设
③ 设![]() 由①②得
由①②得![]()
![]()
![]()
![]() ,
,
![]() 代入③得
代入③得![]()
 的轨迹为
的轨迹为
焦点在y轴上的椭圆.
21、解:(1)![]() 为偶函数
为偶函数 ![]()
![]()
![]()
![]() 为奇函数
为奇函数 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.
的等比数列. ![]()
(2)![]()
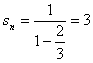
22、解析:(1)如图,以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,![]() A(-1,0),B(1,0)
A(-1,0),B(1,0)
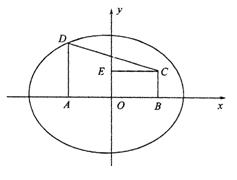
设椭圆方程为:![]()
令![]() ∴
∴
∴ 椭圆C的方程是:![]()
(2)![]() ,
,![]() ,l⊥AB时不符,
,l⊥AB时不符,
设l:y=kx+m(k≠0)
由 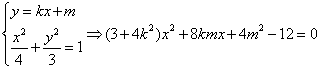
M、N存在![]()
![]()
![]()
设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),MN的中点F(
),MN的中点F(![]() ,
,![]() )
)
∴ ![]() ,
,![]()
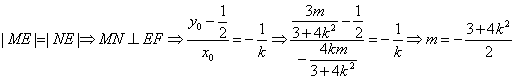
∴![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() 且
且![]()
∴ l与AB的夹角的范围是![]() ,
,![]() .
.
23、(1)![]()
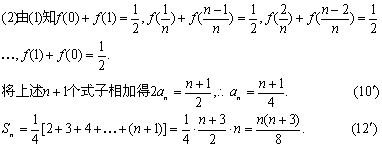
24、(1)当X<0时, ![]()
![]() (3分)
(3分)
(2)函数![]() =
=![]() (X
(X![]() 0)在
0)在![]() 是增函数;(证明略)
(9分)
是增函数;(证明略)
(9分)
(3)因为函数![]() =
=![]() (X
(X![]() 0)在
0)在![]() 是增函数,由x
是增函数,由x![]() 得
得![]() ;
;
又因为![]() ,所以
,所以![]() ,所以
,所以![]() ;
;
因为![]() ,所以
,所以![]() ,且
,且![]() ,即
,即![]() ,
,
所以,-2≤f(x1)
– f(x2) ≤2即![]() -
-![]() <2. (14分)
<2. (14分)
25、解:⑴由题意易得M(-1,0)
设过点M的直线方程为![]() 代入
代入![]() 得
得
![]() ………………………………………(1)
………………………………………(1)
再设A(x1,y1),B(x2,y2)
则x1+x2=![]() ,x1·x2=1
,x1·x2=1
y1+y2=k(x1+1)+k(x2+1)=k(x1+x2)+2k=![]()
∴AB的中点坐标为(![]() )
)
那么线段AB的垂直平分线方程为![]() ,令
,令![]() 得
得
![]() ,即
,即![]()
又方程(1)中△=![]()
⑵若△ABD是正三角形,则需点D到AB的距离等于![]()
![]()
点到AB的距离d=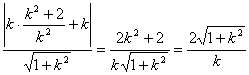
据![]() 得:
得:![]()
∴![]() ,∴
,∴![]() ,满足
,满足![]()
∴△ABD可以为正△,此时![]()
26、解:⑴设E(x,y),D(x0,y0)
∵ABCD是平行四边形,∴![]() ,
,
∴(4,0)+(x0+2,y0)=2(x+2,y)∴(x0+6,y0)=(2x+4,2y)
∴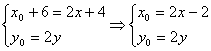
又![]()
即:![]()
∴□ABCD对角线交点E的轨迹方程为![]()
⑵设过A的直线方程为![]()
以A、B为焦点的椭圆的焦距2C=4,则C=2
设椭圆方程为![]() , 即
, 即![]() …………………(*)
…………………(*)
将![]() 代入(*)得
代入(*)得 ![]()
即 ![]()
设M(x1,y1),N(x2,y2)则
![]()
∵MN中点到Y轴的距离为![]() ,且MN过点A,而点A在Y轴的左侧,∴MN中点也在Y轴的左侧。
,且MN过点A,而点A在Y轴的左侧,∴MN中点也在Y轴的左侧。
∴![]() ,∴
,∴![]()
∴![]()
∵![]() ∴
∴![]()
∴![]() 即
即 ![]()
∴![]() ∴
∴![]()
∴![]() ,
, ![]()
![]() ,∵
,∵![]() ,∴
,∴![]()
∴![]()
∴所求椭圆方程为![]()
⑶由⑴可知点E的轨迹是圆![]()
设![]() 是圆上的任一点,则过
是圆上的任一点,则过![]() 点的切线方程是
点的切线方程是![]()
①当![]() 时,
时,![]() 代入椭圆方程得:
代入椭圆方程得:
![]() ,又
,又![]()
∴![]()
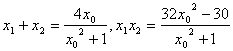
∴![]()
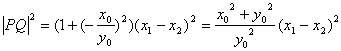
=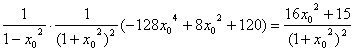
令![]()
则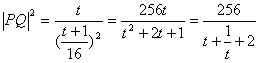 , ∵
, ∵![]()
∴当t=15时, ![]() 取最大值为15 ,
取最大值为15 ,![]() 的最大值为
的最大值为![]() 。
。
此时 ![]() ,∴直线l的方程为
,∴直线l的方程为![]()
②当![]() 时,容易求得
时,容易求得![]()
故:所求![]() 的最大值为
的最大值为![]() ,此时l的方程为
,此时l的方程为![]()
27.解(理)(1)易得l的方程为![]() …1分 由
…1分 由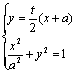 ,得(a2t2+4)y2-4aty=0…2分
,得(a2t2+4)y2-4aty=0…2分
解得y=0或![]() 即点M的纵坐标
即点M的纵坐标![]() ………………4分
………………4分
S=S△AMN=2S△AOM=OA·yM=![]() …7分 (2)由(1)得,
…7分 (2)由(1)得,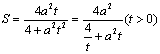
令![]() …………9分 由
…………9分 由![]()
当![]() 时,
时,![]() …10分 若1≤a≤2,则
…10分 若1≤a≤2,则![]() ,故当
,故当![]() 时,Smax=a11分
时,Smax=a11分
若a>2,则![]() 在[1,2]上递增,进而S(t)为减函数. ∴当t=1时,
在[1,2]上递增,进而S(t)为减函数. ∴当t=1时,![]() 13分
13分
综上可得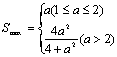 …………14分
…………14分
28. (1) ∵函数f(x)= 的图象过原点,即f(0)=0,∴c =0,∴f(x)= .
又函数f(x)= = b - 的图象关于点(-1,1)成中心对称,∴a=1,b=1,∴f(x)= .(2)由题意有an+1=[ ]2,即 = ,即 = +1,∴ - =1.
∴数列{}是以1为首项,1为公差的等差数列. ∴ =1+(n-1)=n,即 = ,∴an= .∴a2= ,a3= ,a4= ,an= .
29、解:(1)由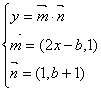 ,得
,得![]() …………2分
…………2分
![]() ,则
,则![]()
![]() …………4分
…………4分
(2)当![]() 时,,
时,,![]()
![]() …………6分
…………6分
![]()
![]() …………8分
…………8分
(3)假设存在符合条件的![]() 使命题成立
使命题成立
当![]() 是偶数时,
是偶数时,![]() 是奇数,则
是奇数,则![]()
由![]() 得
得![]() …………11分
…………11分
当![]() 是奇数时,
是奇数时,![]() 是偶数,则
是偶数,则![]()
由![]() 得
得![]() 无解
无解
综上存在![]() ,使得
,使得![]() …………14分
…………14分
30.解:(1)设![]() ,
,![]() ,直线AB的方程为:
,直线AB的方程为:![]()
把![]() 代入
代入![]() 得:
得:![]()
∴![]() ∴
∴![]()
∴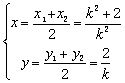 ∴点M的坐标为
∴点M的坐标为![]() ;
;
消去![]() 可得点M的轨迹方程为:
可得点M的轨迹方程为:![]() ;
;
(2)∵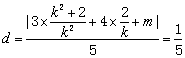
∴![]() ∴
∴![]() ∴
∴![]()
∵![]() ∴
∴![]() ,
,![]() ∴
∴![]() ∴
∴![]()
∴![]() 或
或![]() ∴
∴![]() 或
或![]()
∴![]() ∴
∴![]() 的取值范围为
的取值范围为![]() 。
。