2006年高考数学(理科)模拟试题
|
参考公式:
一. 选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.1+i+i![]() +…+i
+…+i![]() 的值为( )
的值为( )
A.0 B.-1 C.1 D.i
2.若函数f(x)=asin(![]() x+
x+![]() )对任意的x都有
)对任意的x都有
f(![]() )=f(
)=f(![]() ),则f(
),则f(![]() )=( )
)=( )
A.a B-a C.0 D.-a或a
3.不等式![]() <3表示的区域包括(0,0)和(-1,-1),则m的取值范围是
( )
<3表示的区域包括(0,0)和(-1,-1),则m的取值范围是
( )
A.-3<m<3 B.0<m<6 C.-3<m<6 D.0<m<3
4.已知![]() 与
与![]() 为非零向量,下列命题(1)
为非零向量,下列命题(1)![]() (2)
(2)![]() (3)
(3)![]() 且
且![]() //
//![]() .其中可以作为
.其中可以作为![]() =
=![]() 的必要但不充分命题是( )
的必要但不充分命题是( )
A.(2) B.(1)(3) C.(2)(3) D.(1)(2)(3)
5.已知直线![]() 、m,平面
、m,平面![]() 、β,且
、β,且![]() 给出下列命题
给出下列命题
①若![]() ∥β,则
∥β,则![]() ②若
②若![]() ,则
,则![]() ∥β ③若
∥β ③若![]() ⊥β,则
⊥β,则![]() //m ④若
//m ④若![]() ∥m,则
∥m,则![]() ⊥β,其中正确命题的个数是( )
⊥β,其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
6.设0<a<1,实数x,y满足x+![]() =0,则y关于x的函数的图象大致形状是( )
=0,则y关于x的函数的图象大致形状是( )
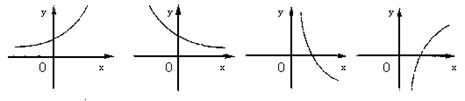
A B C D
7.抛物线x![]() =2y上距离点A(0,a)(a>0)最近的点恰好是顶点,这个结论成立的充要条件是( )
=2y上距离点A(0,a)(a>0)最近的点恰好是顶点,这个结论成立的充要条件是( )
A.a>0 B.![]() C.a
C.a![]() 1
D.0<a
1
D.0<a![]() 1
1
8. 探索以下规律:
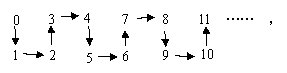
则根据规律,
![]() 从2002到2004,箭头的方向依次是
从2002到2004,箭头的方向依次是
![]()
![]()
![]()
![]()
![]()
![]()
![]() (A) (B) (C) (D)
(A) (B) (C) (D)
9.当x![]() R时,函数f(x)满足
R时,函数f(x)满足![]() ,且
,且![]() ,f(2)=lg15,则f(2004)=(
)
,f(2)=lg15,则f(2004)=(
)
A.-1 B.- lg15 C.1 D. lg ![]()
10.已知x![]() ,不等式
,不等式![]() 恒成立,则实数a的取值范围为( )A
恒成立,则实数a的取值范围为( )A![]() B
B![]() C
C![]() D
D![]()
11. 设随机变量ξ服从正态分布N(0, 1),记Φ(x)=P(ξ< x),则下列结论不正确的是( )
A.Φ(0) =![]() B.Φ(x)=1―Φ(―x)
B.Φ(x)=1―Φ(―x)
C.P(ξ< a) = 2Φ(a) ―1 D.P(ξ> a) = 1―Φ(a)
12.某工厂有100名工人,现需加工5000个甲种零件3000个乙种零件.每个工人每小时能完成4个甲种零件和3个乙种零件.如果你是厂长,为使这批零件尽快完成,应安排加工甲种零件的人数为( )
A.44 B.45 C.44或55 D.55或56
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中的横线上.
13.已知![]() ,则函数y=4
,则函数y=4![]() sinxcosx+cos2x的值域______
sinxcosx+cos2x的值域______
14.在平面直角坐标系中,若方程m(x![]() +y
+y![]() +2y+1)=(x-2y+3)
+2y+1)=(x-2y+3)![]() 表示的曲线是椭圆,则m的取值范围是_____________
表示的曲线是椭圆,则m的取值范围是_____________
15.设f(x![]() )=0,f
)=0,f![]() (x
(x![]() )=
)=![]() ,则
,则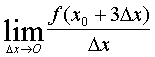 =______
=______
16.在400ml自来水中有1个大肠杆菌,从中随机取出2ml,放到显微镜下观察,发现大肠杆菌的概率是_________
三、解答题:本大题共6小题,满分74分,解答应写出文字说明,证明过程或演算步骤,在相应题目的答题区域内作答.
17.(本小题满分12分)设向量![]() =(1+cosα,sinα),
=(1+cosα,sinα),![]() =(1+cosβ,sinβ),
=(1+cosβ,sinβ),![]() =(1,0),α∈(0,
=(1,0),α∈(0,![]() ),β∈(
),β∈(![]() ,2
,2![]() ),
),![]() 与
与![]() 的夹角为θ1,
的夹角为θ1,![]() 与
与![]() 的夹角为θ2,且θ1―θ2=
的夹角为θ2,且θ1―θ2=![]() ,求
,求![]() 的值
的值
18.(本小题满分12分)甲乙两人独立地破译国际恐怖组织的1个密码,他们能译出的概率分别是![]() 和
和![]() .试求
.试求
1.恰有1个人译出的概率;
2.至多1人译出的概率;
3.若达到译出的概率为![]() ,至少需要多少个乙这样的人?
,至少需要多少个乙这样的人?
19. (本小题满分12分)设f(x) = alnx + bx2 + x在x1=1与x2=2时取得极值,
(1)试确定a、b的值;
(2)求f(x)的单调增区间和减区间;
(3)判断f(x)在x1、x2处是取极大值还是极小值。
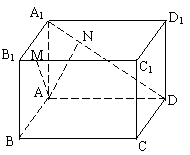 20. (本小题满分12分)如图,在长方体ABCD―A1B1C1D1中,AB=5,AD=8,AA1=
4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求:
20. (本小题满分12分)如图,在长方体ABCD―A1B1C1D1中,AB=5,AD=8,AA1=
4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求:
(1)cos (![]() );
);
(2)直线AD与平面ANM所成的角的大小;
(3)平面ANM与平面ABCD所成角(锐角)的大小.
21. (本小题满分12分)已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足![]() ,
,![]() 。
。
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切线的交点B恒在一条直线上。
22.(本小题满分14分)
已知函数![]() ,设正项数列{
,设正项数列{![]() }的首项
}的首项![]() ,前n项和Sn满足
,前n项和Sn满足![]()
(1)求![]() 的表达式;
的表达式;
(2)在平面直角坐标系内,直线Ln的斜率为an,且Ln与曲线![]() 有且仅有一个公共点,Ln又与y轴交于点Dn(0,bn),当
有且仅有一个公共点,Ln又与y轴交于点Dn(0,bn),当![]()
若![]() 求证:C1+C2+C3…+Cn-n<1.
求证:C1+C2+C3…+Cn-n<1.
参考答案
1.C2.D3.D4.D5.D6.A7.D8.c9.A10.D11.D12.D
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
17.解:∵α∈(0,![]() ),β∈(
),β∈(![]() ,2
,2![]() ), ∴
), ∴![]() ,
,![]()
又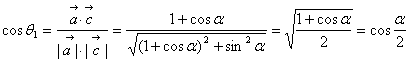 ,
,
![]() ∴
∴![]()
又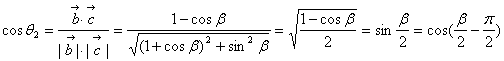
![]() 且
且![]() ,
,![]()
∴![]() ∴
∴![]()
∴![]()
18.(1)![]() (2)
(2)![]() (3)n=17
(3)n=17
19.解(1)令![]() 则2bx2+x+a=0
则2bx2+x+a=0
由题意知:x=1,2是上方程两根,由韦达定理:
 ∴
∴![]()
(2)由(1)知:![]()
令![]() 解得:x<0或1<x<2
解得:x<0或1<x<2
∴f(x)的单调增区间为(1,2) 减区间是(0,1)和(2,+![]() )
)
(3)由(2)知:f(x)在x1=1处取极小值,在x2=2处取极大值。
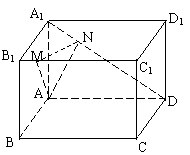 20.
20.
(1)以A为原点,AB、AD、AA1所在直线为x轴,y轴,z轴。
则D(0,8,0),A1(0,0,4),M(5,2,4)
∴![]()
![]()
∵![]() ∴
∴![]()
(2)由(1)知A1D⊥AM,又由已知A1D⊥AN,
∴A1D⊥平面AMN,垂足为N。
因此AD与平面所成的角即是∠DAN。
易知∠DAN = AA1D = arctan2
(3)∵AA1⊥平面ABCD,A1N⊥平面AMN,
∴![]() 和
和![]() 分别成为平面ABCD和平面AMN的法向量。
分别成为平面ABCD和平面AMN的法向量。
设平面AMN与平面ABCD所成的角(锐角)为![]() ,则
,则
![]() =(
=(![]() ,
,![]() )=∠AA1N
= AA1D = arccos
)=∠AA1N
= AA1D = arccos![]()
21.(1)解:设P(a,0),Q(0,b)
则:![]() ∴
∴![]()
设M(x,y)∵![]() ∴
∴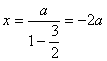
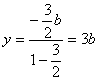
∴![]()
(2)解法一:设A(a,b),![]() ,
,![]() (x1≠x2)
(x1≠x2)
则:直线SR的方程为: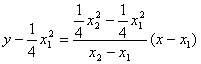 ,
,
即4y = (x1+x2)x-x1x2
∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
对![]() 求导得:y′=
求导得:y′=![]() x
x
∴抛物线上S、R处的切线方程为:
![]() 即4
即4![]() ②
②
![]() 即4
即4![]() ③
③
联立②③,并解之得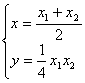 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
故:B点在直线ax-2y-2b=0上
解法二:设A(a,b),当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a)
与![]() 联立消去y得:x2-4kx+4ak-4b=0
联立消去y得:x2-4kx+4ak-4b=0
设![]() ,
,![]() (x1≠x2)
(x1≠x2)
则由韦达定理: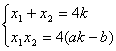
又过S、R点的切线方程分别为:![]() ,
,![]()
联立,并解之得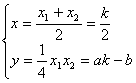 (k为参数)
(k为参数)
消去k,得:ax-2y-2b=0. 故:B点在直线2ax-y-b=0上
22.解:(1)![]() ,
,
所以数列![]() 是以
是以![]() 为首项、
为首项、![]() 为公差的等差数列,……………………2分
为公差的等差数列,……………………2分
![]() ……………………4分
……………………4分
又![]() …………………………………………5分
…………………………………………5分
(2)设Ln: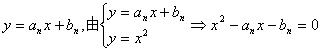 ,
,
据题意方程有相等实根,
![]() …………7分
…………7分
(另解:设Ln与![]() 的公共点为P(
的公共点为P(![]() ),则点P处的切线斜线率
),则点P处的切线斜线率![]()
![]()
令![]() .)
.)
当![]() ……9分
……9分
![]()
…………………………………………………………………………………………11分
![]()
![]() …………………13分
…………………13分
![]() ……………………………………………………………………14分
……………………………………………………………………14分
