中档题过关训练(一)

1、求函数的单调区间，并求f(sinx)的最大值。

2、已知向量=3i-4j，=6i-3j，=(5-m)I-(3+m)j，其中i、j分别是直角坐标系内x轴与y轴正方向上的单位向量。

①若A、B、C能构成三角形，求实数m应满足的条件；

②若△ABC为直角三角形，且∠A为直角，求实数m的值。

3、已知数列{a_n}的前n项之和为S_n，且S_n=a(a_n-1)(a≠0，a≠1，n∈Nⁿ)

(1)求数列{a_n}的通项公式；

(2)数列{b_n}=2n+b(b是常数)，且a₁=b₁，a₂>b₂，求a的取值范围。

4、如图，在三棱锥P-ABC中，PA⊥底面ABC，△ABC为正三角形，D、E分别是BC、CA的中点。

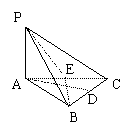(1)证明：平面PBE⊥平面PAC；

(2)如何在BC上找一点F，使AD//平面PEF？并说明理由；

(3)若PA=AB=2，对于(2)中的点F，求三棱锥B-PEF的体积。

5、某种细菌两小时分裂一次，(每一个细菌分裂成两个，分裂所需的时间忽略不计)，研究开始时有两个细菌，在研究过程中不断进行分裂，细菌总数y是研究时间t的函数，记作y=f(t)

(1)写出函数y=f(t)的定义域和值域；

(2)在所给坐标系中画出y=f(t)；(0≤t<6)的图象；

(3)写出研究进行到n小时(n≤0，n∈Z)时细菌的总数有多少个(用关于n的式子表示)。

中档题过关训练(一)

1、f(sinx)有最大值

2、①当m≠时，A、B、C三点能构成三角形；

　　②当m=时，三角形ABC为直角三角形，且∠A=90°。

3、(1)　　　　 (2)

4、(1) ∵PA⊥底面ABC，∴PA⊥BE

又∵△ABC是正三角形，且E为AC的中点，∴BE⊥CA

又PA，∴BE⊥平面PAC∵BE平面PBE，∴平面PBE⊥平面PAC。

(2)取CD的中点F，则点F即为所求。∵E、F分别为CA、CD的中点，∴EF//AD

又EF平面PEF，AD平面PEF，∴AD//平面PEF。(3)

5、 (1)函数y=f(t)的定义域为[0，+∞)；值域为{yy=2ⁿ，n∈N^*}

　　 (2)

　　　(3)y=