2006年高考第一轮总复习试卷
集合与简易逻辑
一、选择题(5×12=60)
1、
已知2a+1<0,关于x的不等式![]() -4ax-5
-4ax-5![]() >0的解集是( )
>0的解集是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2、
已知A={3,a},B=![]() ,A
,A![]() B={1},则A
B={1},则A![]() B等于( )
B等于( )
A、{1,3,a} B、{1,2,3,a} C、{1,2,3} D、{1,3}
3、
满足集合{1,2}![]() M
M![]() {1,2,3,4,5}的集合的个数是( )
{1,2,3,4,5}的集合的个数是( )
A、8 B、7 C、6 D、5
4、
已知非空集合M![]() {1,2,3,4,5},且当
{1,2,3,4,5},且当![]() 时,也有6-
时,也有6-![]() ,则集合M的个数是( )
,则集合M的个数是( )
A、3 B、4 C、5 D、6
5、
若集合A={xx=4n+1,![]() },B={xx=4n-3,
},B={xx=4n-3,![]() },C={xx=8n+1,
},C={xx=8n+1,![]() },则A,B,C的关系是( )
},则A,B,C的关系是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、
已知集合M=![]() ,N=
,N=![]() ,那么y=0时,则有( )
,那么y=0时,则有( )
A、M=N={1,-1} B、M={1,-1},N={(1,0),(-1,0)}
C、M=N={(1,-1)} D、M={1,-1},N ={(1,-1)}
7、 若A、B是两个集合,则下列命题中真命题是( )
A、如果A![]() B,那么A
B,那么A![]() B=B B、如果A
B=B B、如果A![]() B=B,那么A
B=B,那么A![]() B
B
C、如果A![]() B,那么A
B,那么A![]() B=B D、如果A
B=B D、如果A![]() B=B,那么A
B=B,那么A![]() B
B
8、 若命题p的逆命题是q,命题q的否命题是r,则p是r的( )
A、逆命题 B、逆否命题 C、否命题 D、以上判断都不对
9、 用反证法证明命题:若整数系数一元二次方程![]()
![]() 有有理数根,那么a,b,c中至少有一个是偶数时,下列假设中正确的是( )
有有理数根,那么a,b,c中至少有一个是偶数时,下列假设中正确的是( )
A、假设a,b,c都是偶数
B、假设a,b,c都不是偶数
C、假设a,b,c至多有一个是偶数
 D、假设a,b,c至多有两个是偶数
D、假设a,b,c至多有两个是偶数
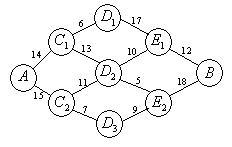
10、如图是一人出差从A城出发到B城去,沿途可能经过的城市的示意图。通过两城市所需时间标在两城市之间的连线上(单位:时),则此人从A城出发到B城所需时间最少要( )小时。
A.48 B.49 C.50 D.46
11、 四个孩子在罗老师的后院玩球,突然传来一阵打碎玻璃的响声,罗老师跑去察看,发现一扇窗户玻璃被打破了,老师问:“谁打破的?”宝宝说:“是可可打破的。”可可说:“是毛毛打破的。”毛毛说:“可可说谎。”多多说:“我没有打破窗子。”如果只有一个小孩说的是实话,那么打破窗户玻璃的应该是( )。
A.多多 B.毛毛 C.可可 D.宝宝
12、已知全集U=R,A![]() U,B
U,B![]() U,如果命题P:
U,如果命题P:![]()
![]() A
A![]() B,则命题“
B,则命题“![]() ”是( )
”是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
二、填空题(4×4=16)
13、已知A:![]() ,B:
,B:![]() >0,则
>0,则![]() 是
是![]() 的______________条件。
的______________条件。
14、已知集合A=![]() ,B=
,B=![]() 且A
且A![]() B={x0<x
B={x0<x![]() 2},A
2},A![]() B={xx>-2},则a=____________,b=_____________。
B={xx>-2},则a=____________,b=_____________。
15、若命题p:一元一次不等式ax+b>0的解集为{xx>![]() },命题q:关于x的不等式(x-a)(x-b)<0的解集为{xa<x<b},则“p且q”,“p或q”,“非p”形式的复合命题中的真命题是____________________
。
},命题q:关于x的不等式(x-a)(x-b)<0的解集为{xa<x<b},则“p且q”,“p或q”,“非p”形式的复合命题中的真命题是____________________
。
16、某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆,为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取______,_______,_______辆.
三、解答题(17-21题每题12分,22题14分)
17、已知集合M={2,a,b},N={2a,2,![]() },其中M=N,求a,b的值。
},其中M=N,求a,b的值。
18、已知集合A={![]() },B ={
},B ={![]() },若
},若![]() ,求实数a的值。
,求实数a的值。
19、设有两个命题:(1)不等式x+x-1>m的解集为R;(2)函数f(x)=-![]() 是减函数。如果这两个命题中有且只有一个真命题,求实数m的取值范围。
是减函数。如果这两个命题中有且只有一个真命题,求实数m的取值范围。
20、已知a为实数,集合A=![]() ,B=
,B=![]() ,C=
,C=![]() ,求a使得
,求a使得![]() 且
且![]() .
.
21、已知p:![]() ,q:
,q:![]() (m>0)若
(m>0)若![]() 是
是![]() 的充分不必要条件,求实数m的取值范围。
的充分不必要条件,求实数m的取值范围。
22、已知下列三个方程![]() ,
,![]() ,
,![]() 中至少有一个方程有实根,求实数a的取值范围。
中至少有一个方程有实根,求实数a的取值范围。
23、(选做题15分)已知二次函数![]() 的图像经过点(-1,0),是否存在常数a,b,c使得不等式
的图像经过点(-1,0),是否存在常数a,b,c使得不等式![]() 对一切实数x都成立?若存在,求出a,b,c;若不存在,请说出理由。
对一切实数x都成立?若存在,求出a,b,c;若不存在,请说出理由。
参考答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | C | D | C | B | C | B | B | A | A | D |
13、必要而不充分
14、a=1,b=-2
15、非P
16、6,30,10
17、a=0,b=1;a=![]() ,b=
,b=![]()
18、![]()
19、![]()
20、a=-2
21、![]()
22、![]() 或
或![]()
23、存在,![]() ,
,![]()
