综合题解法集锦
要点:所谓综合题,是泛指题目本身或在解题过程中,涉及多个知识点和多种数学思想方法、具有较高能力要求的数学题.
如下,我们从八个方面举例,对综合题的解题策略作一探讨.
一、从条件入手——分析条件,化繁为简,注重隐含条件的挖掘.
二、从结论入手---执果索因,搭好联系条件的桥梁.
三、回到定义和图形中来.
四、以简单的、特殊的情况为突破口.
五、构造辅助问题(函数、方程、图形……),换一个角度去思考.
六、通过横向沟通和转化,将各数学分支中不同的知识点串联起来.
七、培养整体意识,把握整体结构。
八、连续性问题——承上启下,层层递进,充分利用已得出的结论.
【例题示范】
1、成等差数列的四个数之和为26,第二数和第三数之积为40,求这四个数.
解:设四个数为![]()
则:![]()
由①: ![]() 代入②得:
代入②得: ![]()
∴ 四个数为2,5,8,11或11,8,5,2.
2、在等差数列![]() 中,若
中,若![]() 求
求![]() .
.
解:∵![]() ∴
∴ ![]() 而
而![]()
3、已知等差数列的前![]() 项和为
项和为![]() ,前
,前![]() 项和为
项和为![]() ,求前
,求前![]() 项和.
项和.
解:由题设 ![]()
![]()
∴![]() 而
而
![]()
从而:
![]()
![]()
4、已知![]() ,
,![]()
![]() 求
求![]() 及
及![]() .
.
解:![]() 从而有
从而有![]()
∵![]() ∴
∴![]()
![]()
![]()
![]()
∴![]() ∴
∴![]()
5、已知![]() 求
求![]() 的关系式及通项公式
的关系式及通项公式![]()
解: ![]()
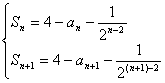
![]() ②-①:
②-①:![]() 即:
即:![]()
将上式两边同乘以![]() 得:
得: ![]()
即:![]()
显然:![]() 是以1为首项,1为公差的AP
是以1为首项,1为公差的AP
∴ ![]()
∴
![]()
6、已知![]() ,求
,求![]() 及
及![]() .
.
解:∵![]() ∴
∴
![]() ∴
∴![]()
设![]() 则
则![]() 是公差为1的等差数列 ∴
是公差为1的等差数列 ∴![]()
又:∵![]() ∴
∴![]() ∴
∴![]()
当![]() 时
时 ![]()
∴![]()
![]()
![]()
7、设![]() 求证:
求证:![]()
证:∵ ![]()
![]()
∴ ![]()
∴ ![]()
∴![]()
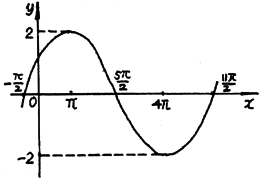
8、已知函数![]() 的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(
的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(![]() )和(
)和(![]() ).
).
(I)求![]() 的解析式;
的解析式;
(II)用列表作图的方法画出函数y=f(x)在长度为一个周期的闭区间上的图象.
解:(Ⅰ)由已知,易得A=2.
![]() ,解得
,解得![]() .
.
把(0,1)代入解析式![]() ,得
,得
![]() .又
.又![]() ,解得
,解得![]() .
.
∴![]() 为所求.…………………………………………6分
为所求.…………………………………………6分
(Ⅱ)
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
| 0 | 2 | 0 |
| 0 |
9、已知函数![]() .
.
(I)指出![]() 在定义域R上的奇偶性与单调性(只须写出结论,无须证明);
在定义域R上的奇偶性与单调性(只须写出结论,无须证明);
(II)若a、b、c∈R,且![]() ,试证明:
,试证明:![]() .
.
解:(Ⅰ)![]() 是定义域
是定义域![]() 上的奇函数且为增函数.
上的奇函数且为增函数.
(Ⅱ)由![]() 得
得![]() .由增函数,得
.由增函数,得![]()
由奇函数,得![]() ∴
∴![]()
同理可得 ![]()
将上三式相加后,得![]() .
.
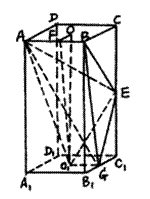
10、已知:如图,长方体ABCD—![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,E为
,E为![]() 的中点,
的中点,![]() 为下底面正方形的中心.求:(I)二面角C—AB—
为下底面正方形的中心.求:(I)二面角C—AB—![]() 的正切值;
的正切值;
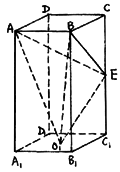 (II)异面直线AB与
(II)异面直线AB与![]() 所成角的正切值;
所成角的正切值;
(III)三棱锥![]() ——ABE的体积.
——ABE的体积.
解:(Ⅰ)取上底面的中心![]() ,作
,作![]() 于
于![]() ,连
,连![]() 和
和![]() .
.
由长方体的性质,得![]() 平面
平面![]() ,由三垂线定理,
,由三垂线定理,
得![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角
的平面角
![]() .
.
在![]() 中,
中,![]()
(Ⅱ)取![]() 的中点G,连
的中点G,连![]() 和
和![]() .
.
易证明![]() ,则
,则![]() 为所求
为所求
![]() .
.![]() .
.
在![]() 中,
中,![]()
(Ⅲ)连![]() ,
,![]() ,由
,由![]() 易证明
易证明![]() 平面
平面![]() .
.
![]()
![]() ∴
∴![]()
11、已知等差数列{![]() }的公差为d,等比数列{
}的公差为d,等比数列{![]() }的公比为q,且,
}的公比为q,且,![]() (
(![]() ),若
),若![]() ,求a的取值.
,求a的取值.
解:由![]() 得
得![]() ,
,![]()
由已知,得![]()
![]()
∵![]() ,∴
,∴![]() 由对数定义得
由对数定义得![]()
当![]() ,
,![]() 时,得
时,得![]() ,
,![]() .
.
当![]() ,
,![]() 时,得
时,得![]() .这与已知
.这与已知![]() 相矛盾.
相矛盾.
当![]() ,
,![]() 时,得
时,得![]() .
.
综上:当![]() 时,
时,![]()
当![]() ,
,![]() 时,
时,![]() 的取值集合为空集
的取值集合为空集
当![]() ,
,![]() 时,
时,![]()
12、已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,如图:
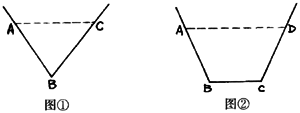
图①的过水断面为等腰△ABC,AB=BC,过水湿周![]()
图②的过水断面为等腰梯形![]() ∥
∥![]() ,过水湿周
,过水湿周![]() .若
.若![]() 与梯形ABCD的面积都为S,
与梯形ABCD的面积都为S,
(I)分别求![]() 的最小值;
的最小值;
(II)为使流量最大,给出最佳设计方案.
解(Ⅰ)在图①中,设![]() ,
,![]() .
.
则![]() .由于
.由于![]() 、
、![]() 、
、![]() 皆为正值,可解得
皆为正值,可解得![]() .
.
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
所以![]() .
.
在图②中,设![]() ,
,![]() .
.![]() 可求得
可求得
![]() ,
,![]()
解得![]() .
.
![]() .
.
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
(Ⅱ)由于![]() ,则
,则![]() 的最小值小于
的最小值小于![]() 的最小值.
的最小值.
所以在方案②中当![]() 取得最小值时的设计为最佳方案.
取得最小值时的设计为最佳方案.
13、已知:如图,射线OA为y=2x(x>0),射线OB为y= –2x(x>0),动点P(x, y)在![]() 的内部,
的内部,![]() 于N,四边形ONPM的面积为2..
于N,四边形ONPM的面积为2..
(I)动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
 (II)确定y=f(x)的定义域.
(II)确定y=f(x)的定义域.
解:(Ⅰ)设![]() ,
,![]()
![]() .
.
则![]() ,
,![]()
由动点![]() 在
在![]() 的内部,得
的内部,得![]() .
.
∴![]() ,
,![]()
∴![]()
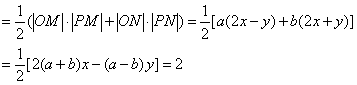
∴![]() ①
①
又![]() ,
,![]()
分别解得![]() ,
,![]()
代入①式消去![]() 、
、![]() ,并化简得
,并化简得![]() .
.
∵![]() ,∴
,∴![]() .
.
(Ⅱ)由![]() 在
在![]() 内部,得
内部,得![]() .
.
又垂足![]() 必须在射线
必须在射线![]() 上,否则
上,否则![]() 、
、![]() 、
、![]() 、
、![]() 四点不能构成四边形,所以还必须满足条件
四点不能构成四边形,所以还必须满足条件![]()
∴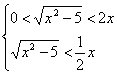
![]()
![]()
所以![]() 的定义域为
的定义域为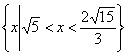
14、解关于x的不等式:loga(x2-x-2)>loga(x-![]() )+1(a>0,a≠1)
)+1(a>0,a≠1)
解:原不等式等价于![]() ……①
……①
1°当![]() 时,①式可化为
时,①式可化为
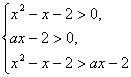 从而
从而![]() 即
即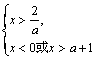
∴![]()
2°当![]() 时,①式可化为
时,①式可化为
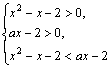 从而
从而![]() 即
即![]() ∴
∴![]() Φ
Φ
综上所述,当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;当
;当![]() 时,不等式的解集为Φ
时,不等式的解集为Φ
15、在三角形ABC中,三内角满足A+C=2B,![]() ,求cos
,求cos![]() 的值
的值
解:∵A+C=2B,∴A+C=120°,B=60°
又∵![]() ,∴
,∴![]()
∴![]()
即![]()
![]()
令![]() ,则上式为
,则上式为![]()
∴![]()
∵![]() ,∴
,∴![]()
16、已知复数z1=2-![]() x+xi,z2=
x+xi,z2=![]() y—1+(
y—1+(![]() -y)i,x、y属于R,若z1=z2且argz1/z2=90º,求
-y)i,x、y属于R,若z1=z2且argz1/z2=90º,求![]() 的值
的值
解:∵![]() ∴
∴![]()
∴![]()
![]() ∴
∴![]()
解得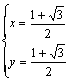
∴![]() ,
,
![]()
∴![]()
![]()
∴![]()
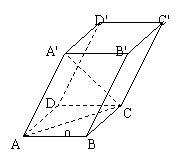 17、如图,平行六面体ABCD-A'B'C'D'中,AC=2
17、如图,平行六面体ABCD-A'B'C'D'中,AC=2![]() ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
(1)求侧棱AA'与底面ABCD所成角的大小;
(2)求侧面A'ADD'底面ABCD所成二面角的正切值;
(3)求四棱锥C-A'ADD'的体积.
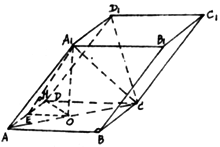
解:(I)连![]() ,则
,则![]() 平面
平面![]() 于
于![]()
∴![]() 就是侧棱
就是侧棱![]() 与底面
与底面![]() 所成的角
所成的角
在![]() 中,
中,![]()
![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]() ,即侧棱
,即侧棱![]() 与底面
与底面![]() 所成角为45°,
所成角为45°,
(II)在等腰![]() 中,
中,![]() ,∴
,∴![]() ,且O为AC中点,
,且O为AC中点,
过O作![]() 于E,连
于E,连![]() 。∵
。∵![]() 平面ABCD于O,
平面ABCD于O,
由三垂线定理,知![]() ,
,
∴∠![]() 是侧面
是侧面![]() 与底面ABCD所成二面角的平面角。
与底面ABCD所成二面角的平面角。
∵∠ABC=![]() ,
,![]() ,∴底面ABCD是正方形。
,∴底面ABCD是正方形。
∴![]()
![]()
![]() 。 在
。 在![]() 中,
中,![]() 。
。
即所求二面角的正切值为![]() 。
。
(Ⅲ)由(Ⅱ)知,![]()
![]() 。
。
∴![]() 。
。
∵![]() ,∴
,∴![]() 。
。
∵![]() ,∴平面
,∴平面![]() ,它们的交线是
,它们的交线是![]() 。
。
过O作![]() ,则
,则![]() 。
。
![]() 。
。
又∵![]() 的中点,∴点C到平面
的中点,∴点C到平面![]() 的距离
的距离![]() 。
。
∴![]() 。
。
另解:![]() 。
。
18、在工厂生产中,若机器更新过早,则生产潜力未能充分发挥而造成浪费;若更新过迟,老机器生产效率低,维修与损耗费用大,也会造成浪费.因此,需要确定机器使用的最佳年限(即机器使用多少年平均费用最小)
某工厂用7万元购买了一台新机器,运输安装费2千元,每年投保、动力消耗固定的费用为2千元;每年的保养、维修、更换易损件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,……,即每年增加1千元,问这台机器的最佳使用年限是多少年?并求出年平均费用的最小值.
解:设使用![]() 年为最佳年限,则每年的平均费用
年为最佳年限,则每年的平均费用![]()
![]()
![]()
![]()
![]() (万元)。
(万元)。
当且仅当![]() ,即
,即![]() ,即
,即![]() 时取等号。
时取等号。
答:这台机器最佳使用年限为12年,且年平均费用的最小值为1.55万元。
19、已知数列{an}满足a1=2,对于任意的n∈N,都有an>0,
且(n+1)a![]() +anan+1-na
+anan+1-na![]() =0,又知数列{bn}:b1=2n-1+1
=0,又知数列{bn}:b1=2n-1+1
(1)求数列{an}的通项an以及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn和Tn的大小关系,并说明理由.
解:(Ⅰ)∵![]()
∴![]() 。
。
∴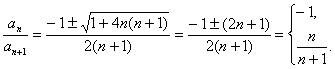
∴![]() ,∴
,∴![]() 。 即
。 即![]() 。
。
∴![]()
![]() 。
。
∴![]() ,∴又
,∴又![]() ,∴
,∴![]() 。
。
∴![]()
![]() 。
。
(Ⅱ)∵![]() ,
,
∴![]()
![]()
![]() 。
。
(Ⅲ)![]()
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() 。
。
猜想:当![]() 时,
时,![]() 。 即
。 即![]() 。亦即
。亦即![]() 。
。
下面用数学归纳法证明:
![]() 当
当![]() 时,前面已验证成立;
时,前面已验证成立;
![]() 假设
假设![]() 时,
时,![]() 成立,那么当
成立,那么当![]() 时,
时,
![]()
![]()
![]()
![]() 。
。
∴当![]() 时,
时,![]() 也成立。
也成立。
由以上![]() 、
、![]() 可知,当
可知,当![]() 时,有
时,有![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
20、将两副三角板放成如图所示的形状,使二面角D-AC-B成直二面角。
已知:BC=CD,∠ACD=∠ABC=900.求:二面角C-AB-D的大小。
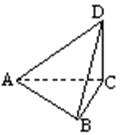 证:如图∵平面ACD^平面ABC,CD^AC,
证:如图∵平面ACD^平面ABC,CD^AC,
∴CD^平面ABC.
∵斜线BD在平面ABD上的射影为BC,AB^BC,
∴AB^BD.即∠DBC为二面角
C-AB-D的平面角。
∵BC=CD,CD^BC,∴∠DBC=450翰林汇
21、正方形ABCD和正方形ABEF折成一个二面角,M、N分别是对角线AC和BF上的点,且AM=FN(如图),求证:MN//平面BEC.
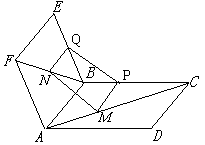 证明:如图,分别过M、N作
证明:如图,分别过M、N作
MP∥DC交BC于P,NQ ∥EF交
EB于Q,连接PQ ∵EF∥AB∥CD,∴MP∥NQ
又∵AM=FN,∴在正方形ABEF
和正方形ABCD中,MP=NQ
∴ 四边形 MPQN为平行四边形
∴MN∥PQ,∵![]()
∴MN∥平面EBC
22、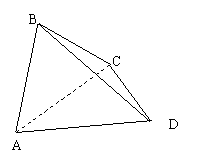
 矩形ABCD(AB≤BC)中,AC=2
矩形ABCD(AB≤BC)中,AC=2![]() ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=![]() ,求AB、BC的长.
,求AB、BC的长.
翰林汇
翰林汇解:如图,
分别过B、D作BE⊥AC于E,DF⊥AC于F,
设∠BAC=θ,则AB=ACcosθ=2cosθ,
BE=DE=ABsinθ=sin2θ,
AE=ABcosθ=2cos2θ∴EF=AC-2AE
=2=-2cos2θ
折叠后,在平面ACD内过E作EG∥FD,且EG=FD,连接DG、BG、BD,则∠BEG为二面角B-AC-D的平面角,∴∠BEG=90°
于是BG=BE=sin2θ=2sin2θ
∴BG2+DG2=BD2,即:(2sin2θ)2+(-2cos2θ)2=5
∴4(cos2θ)2=1,∴cos2θ=±,
∵AB≤BC,∴cos2θ=-∴cosθ=,故AB=![]() ,BC=
,BC=![]()
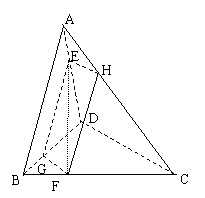 23、在三棱锥A-BCD中,E、F分别是线段AD、BC上的点,满足
23、在三棱锥A-BCD中,E、F分别是线段AD、BC上的点,满足![]() ,AB=CD=3,且AB与CD所成的角为60o,求EF的长.
,AB=CD=3,且AB与CD所成的角为60o,求EF的长.
解:如图,过E 分别作EG∥AB
交BD于G,EH∥DC交AC于H,
连接GH、FH,由条件,易知
EGFH为平行四边形。
∴∠GEH为异面直线AB与CD
所成的角或其补角。∴∠GEH=60°或120°
又EG=AB=2,EH=AB=1,
由余弦定理得:EF==![]() 或
或![]()
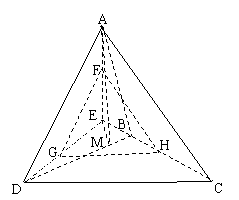
翰林汇24、如图,△ABC和△DBC所在平面互相垂直 ,AB=BC=BD,∠CBA=∠DBC=120o,求
(1) AD与平面BCD的成角;
(2) AD与BC的成角;
(3) 二面角A-BD-C的正切值.
解:(1)如图,过A作AE⊥CB与CB的延长线交与E,连接DE,
∵平面ABC⊥平面DBC∴AE⊥平面DBC,
 ∴∠ADE即为AD与平面CBD所成的角。
∴∠ADE即为AD与平面CBD所成的角。
∵AB=BD,∠CBA=∠DBC,EB=EB
∴∠ABE=∠DBE,∴△DBE≌△ABE
∴DE⊥CB且DE=AE
∴∠ADB=45°∴AD与平面CBD
所成的角为45°
(2)由(1)知CB⊥平面ADE
∴AD⊥BC即AD与BC所成的角为90°.
(3)过E作EM⊥BD于M
由(2)及三垂线定理知,AM⊥BD,
∴∠AME为二面角A-BD-C的平面角的补角.
∵AE=BE=2ME,∴tg∠AME=2,故二面角A-BD-C的正切值为-2.
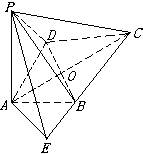
25、如图:已知平面四边形ABCD,AC、BD相交于O,AB=AD,CB=CD,
∠ABC=120°,且PA⊥平面ABCD.
(1)若AB=PA=![]() ,求P到直线BC的距离;
,求P到直线BC的距离;
(2)求证平面PBD⊥平面PAC.
证明(1)延长CB,过A在平面![]() 内作AE⊥CB,垂足为E.
内作AE⊥CB,垂足为E.
∵∠ABC=120°,∴∠ABE=60°,在Rt△ABE中:AE=AB·sin60°=![]() ·
·![]() =
=![]()
∵PA⊥平面![]() ,AE⊥EB,∴AE是PE在平面
,AE⊥EB,∴AE是PE在平面![]() 内的射影,
内的射影,
∴PE⊥EB,∴PE为点P到BC的距离.在Rt△PAE中:
 PE=
PE=![]() .
.
(2)在四边形ABCD中,取BD中点O,连AO、CO,
∵AB=AD,CD=CB,BO=OD,
∴AO⊥BD,CO⊥BD, ∴A、O、C共线,∴AC⊥BD.
又PA⊥![]() ,∴PA⊥BD,
,∴PA⊥BD,
∴BD⊥平面PAC,∵BD![]() 平面PBD, ∴平面PBD⊥平面PAC.
平面PBD, ∴平面PBD⊥平面PAC.
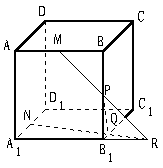
26、如图,正方体ABCD-A1B1C1D1的棱长为8cm,M、N、P分别是AB、A1D1、BB1的中点;(1)画出过M、N、P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线;(2)设过M、N、P三点的平面与B1C1交于点Q,求PQ的长;
解:(1)设M、N、P三点确定的平面为α,则α与平面AA1B1B的交线为直线MP,设![]() ,则RN是α与平面A1B1C1D1的交线,设
,则RN是α与平面A1B1C1D1的交线,设![]() ,则直线PQ就是所要画的平面α与平面BB1C1C的交线;
,则直线PQ就是所要画的平面α与平面BB1C1C的交线;

(2)正方体的棱长为8cm,B1R=BM=4cm,![]() ,
,
故B1Q=![]() 4=
4=![]() (cm),在Rt△PB1Q中,B1P=4cm,B1Q=
(cm),在Rt△PB1Q中,B1P=4cm,B1Q=![]() cm,
cm,

![]() (cm)
(cm)
27、如图,四棱锥V-ABCD中,∠BCD=∠BAD=90°,
又∠BCV=∠BAV=90°,求证:VD⊥AC;
证明:∠BCD=∠BAD=90°![]() BC⊥CD,BA⊥AD
BC⊥CD,BA⊥AD
∠BCV=∠BAV=90°![]() BC⊥CV,BA⊥AV,
BC⊥CV,BA⊥AV,
∴BC⊥平面VCD,BA⊥平面VAD ∴BC⊥VD,BA⊥VD
∴VD⊥平面ABC,∴VD⊥AC
28、过点S引三条长度相等不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,
∠BSC=90°,求证:平面ABC⊥平面BSC。
证明:作AO⊥平面SBC,O为垂足,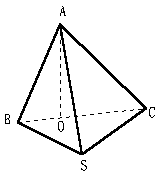
∵SA=SB,∠ASB=60°,∴AB=AS,同理AS=AC,∴AB=AS=AC,∴O为△BSC的外心,又∠BSC=90°,故O为BC中点,即AO在平面ABC内,所以平面ABC⊥平面BSC。
29、三棱锥P-ABC中,三侧棱PA、PB、PC两两相互垂直,三侧面面积分别为S1、S2、S3,底面积为S,三侧面与底面分别成角α、β、γ,(1)求S(用S1、S2、S3表示);(2)求证:cos2α+cos2β+cos2γ=1;

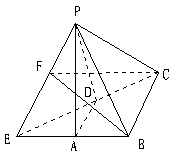 解:设PA=a,PB=b,PC=c,则S1=
解:设PA=a,PB=b,PC=c,则S1=![]() ab ,S2=
ab ,S2=![]() bc,S3=
bc,S3=![]() ca,
ca,
作PD⊥BC于D,连AD,易证BC⊥平面PAD,
于是BC⊥AD;S△ABC=![]() BC×AD,在Rt△APD中,AD2=a2+PD2,
BC×AD,在Rt△APD中,AD2=a2+PD2,
在Rt△BPC中,PD2=![]() ,
,
∴AD2=a2+![]()
∴S△ABC2=(![]() BC×AD)2=
BC×AD)2=![]() (a2b2+b2c2+c2a2)=
(a2b2+b2c2+c2a2)=![]()
∴![]()
证明:由(1)知,PD⊥BC,AD⊥BC,∴∠PDA是侧面PBC与底面ABC所成二面角的平面角,不妨设∠PDA=α,
PD2=![]() ,AD2=
,AD2=![]()
∴cos2α=![]() ;同理cos2β=
;同理cos2β=![]() ;
;
cos2γ=![]() ;∴cos2α+cos2β+cos2γ=1
;∴cos2α+cos2β+cos2γ=1
30、如图,四棱锥P-ABCD的侧棱PA⊥底面ABCD,底面ABCD是直角梯形,其中∠DAB=∠CBA=90°,又AD=AB=![]() BC,∠APB=arcsin
BC,∠APB=arcsin![]() ,试求侧面APB与侧面CPD所成的角。
,试求侧面APB与侧面CPD所成的角。
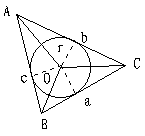 解:设AD=AB=
解:设AD=AB=![]() BC=3a,由Rt△PAB≌Rt△PAD,∠APB=arcsin
BC=3a,由Rt△PAB≌Rt△PAD,∠APB=arcsin![]() ,得PD=PB=5a,PA=4a,延长CD、BA交于E,连PE,作BF⊥PE于F,连CF,可证BC⊥平面PBE,则CF⊥PE(
三垂线定理),从而∠BFC是二面角B-PE-C的平面角,设其为θ; 显然AD是△EBC的中位线,∴EA=AB=3a,即EB=6a,可得PE=PB=5a
,得PD=PB=5a,PA=4a,延长CD、BA交于E,连PE,作BF⊥PE于F,连CF,可证BC⊥平面PBE,则CF⊥PE(
三垂线定理),从而∠BFC是二面角B-PE-C的平面角,设其为θ; 显然AD是△EBC的中位线,∴EA=AB=3a,即EB=6a,可得PE=PB=5a
在△PBE中,用面积关系得:PE×BF=BE×PA
∴BF=![]()
由Rt△BCF,![]() ,∴
,∴![]() ;
;
本题还可以用射影面积法。
31、多面体表面积为S,外切于表面积为36π(平方单位)的球,求这个多面体的体积;
分析:可仿照平面几何类似问题,连结三角形的内切圆圆心和各个顶点的线段,将三角形面积分为三个部分,且有S=![]() r(a+b+c);
r(a+b+c);
解:球的半径R=3,连结球心和多面体各个顶点
,得到的锥体体积之和就是多面体的体积,这些锥体的高都是半径R,故V=![]() =S(立方单位)。
=S(立方单位)。
32、给定一个圆锥和两个平面α、β,其中α∥β,且它们与圆锥底面平行,若平面α把圆锥侧面分成面积相等的两部分,平面β把圆锥分成体积相等的两部分,求夹在α、β间的几何体的体积与圆锥体积之比。
分析:本题涉及到截锥性质:截面积与底面积的比为对应元素的平方比,截得的圆锥的体积与原圆锥的体积之比是对应元素的立方比。
解:设给定圆锥的底面半径为R,高为H,则V圆锥=![]() πR2H;
πR2H;
设平面α、β与圆锥侧面相交所得两圆半径分别为r1和r2,
由截锥性质得:![]()
显然r2>r1,即平面β比平面α离圆锥底面近些,又设截得的两圆锥的高分别是h1和h2,则夹在α、β间的圆台的高h,有:
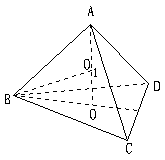 h= h2-h1=
h= h2-h1=![]() ;
;
V圆台=![]() π×
π×![]() ×(
×(![]() )
)
=![]() ×
×![]() πR2H
πR2H
∴V圆台:V圆锥=![]()
33、在一个每边长均为1的正三棱锥内部有13个点,其中任三点不共线,任四点不共面,试证:其中至少有一个以这些点中的四个点为顶点的三棱锥,其体积V![]()
证明:设棱长均为1的正三棱锥为A-BCD,AO是它的高,今在AO上取一点O1,使O1A=O1B=O1C=O1D,可求得OB=![]() ,AO=
,AO=![]() ,
,
进而求得O1A=O1B=O1C=O1D=![]() ;
;
以O1为点,以A-BCD得四个面为底面的四个三棱锥显然等积,且V'=![]() ;
;
在三棱锥内部的13个点,因为其中任三点不共线,任四点不共面,由抽屉原理,至少有四点落在以O1为顶点的四个小三棱锥的同一个三棱锥内,那幺这四点为顶点的三棱锥的体积V![]() 。
。
34、进货原价为80元的商品400个,按90元一个售出时,可全部卖出。已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?
解:设售价为![]() 元时利润为
元时利润为![]() ,此时售量为
,此时售量为![]()
![]()
当![]() 时,
时,![]() (元)。
(元)。
答:售价为95元时获利最大,其最大值为4500元。
35、20个劳动力种50亩地,这些地可种蔬菜、棉花、水稻。这些作物每亩地所需劳力和预计产值如下表。应怎样计划才能使每亩地都能种上作物(水稻必种),所有劳力都有工作且作物预计总产值达最高?
| 作物 | 劳力/亩 | 产值/亩 |
| 蔬菜 | 1/2 | 0.6万元 |
| 棉花 | 1/3 | 0.5万元 |
| 水稻 | 1/4 | 0.3万元 |
解:设种![]() 亩水稻(0<x≤50),
亩水稻(0<x≤50),![]() 亩棉花(0<x≤50)时,总产值为
亩棉花(0<x≤50)时,总产值为![]() 且每个劳力都有工作。
且每个劳力都有工作。
![]() 且
且![]() 、
、![]() 满足
满足![]()
即![]()
欲使![]() 为最大,则
为最大,则![]() 应为最小,故当
应为最小,故当![]() (亩)时,
(亩)时,![]() 万元,此时
万元,此时![]() (亩)。
(亩)。
故安排1人种4亩水稻,8人种24亩棉花,11人种22亩蔬菜时农作物总产值最高且每个劳力都有工作。
36、某企业在今年年初向银行贷款![]() 万元,年利率为
万元,年利率为![]() ;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
解:设平均每年末应向银行偿还![]() 万元,则每年尚欠银行款依次为:
万元,则每年尚欠银行款依次为:
![]()
……
第五年欠款应等于零,即:
![]() …
…![]()
∴![]() 故平均每年末向银行偿还金额
故平均每年末向银行偿还金额![]() 万元。
万元。
37、某市1994年底人口为20万,人均住房面积为8![]() ,计划1998年底人均住房面积达10
,计划1998年底人均住房面积达10![]() 。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万
。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万![]() (结果以万
(结果以万![]() 为单位,保留两位小数)。
为单位,保留两位小数)。
解:设平均每年至少要新增住房面积![]() 万
万![]() 。四年共新增住房面积4
。四年共新增住房面积4![]() 万
万![]() 。此时住房总面积应为
。此时住房总面积应为![]() 万
万![]() 。另一方面,到1998年底总人口为20(1+1%)4万。按人均10
。另一方面,到1998年底总人口为20(1+1%)4万。按人均10![]() 计,1998年底应有住房面积为20×10×(1+1%)4万
计,1998年底应有住房面积为20×10×(1+1%)4万![]() 。据题意有:
。据题意有:
![]()
因![]() 故
故![]() 即
即![]()
故该城市每年至少要新增住房面积12、03万![]() ,才可达人均住房面积10
,才可达人均住房面积10![]() 的目标。
的目标。
38、铁道机车运行1小时所需的成本由两部分组成,固定部分为![]() 元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
元,变动部分与运行速度V(千米/小时)的平方成正比。比例系数为k(k≠0)。如果机车匀速从甲站开往乙站,为使成本最省应以怎样的速度运行?
解:设以速度V匀速运行成本最省,甲、乙两站相距S千米,则机车匀速从甲站到乙站所需时间为![]() 总成本为
总成本为![]() 元。
元。
![]()
仅当![]() 时,
时,![]() 有最小值,
有最小值,
故机车以速度![]() 千米/小时匀速运行时,成本最省。
千米/小时匀速运行时,成本最省。
39、某渔场养鱼,鱼的重量增长率第一年为400%,以后每年重量增长率都是前一年的三分之一。同时鱼每年要损失预计重量的10%。预计养鱼的费用第一年是鱼苗成本的20%,以后每年的费用M(t)与年数t满足关系式![]() (其中
(其中![]() 为鱼苗成本,
为鱼苗成本,![]() )。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
)。问该渔场的鱼养几年后全部捕捞,鱼的产值高且费用较少(设鱼苗价30元/斤,成鱼市场价7元/斤)。
解:设第![]() 年鱼的产值
年鱼的产值![]() 为最高。p为鱼苗总重量,则
为最高。p为鱼苗总重量,则
![]() ,
,
![]()

![]() ……,
……,
![]()
当![]()
即第4年鱼的产值最高;另一方面,
![]()
当![]() 或4时,
或4时,![]()
下面比较第4年比第3年增加的产值G与该年投入的费用![]() 的大小。
的大小。
若G≠0则取![]() ;
;
若![]() 则取
则取![]()
![]()
∴取![]() ,即该渔场三年后捕捞,鱼的总产值高且费用较少。
,即该渔场三年后捕捞,鱼的总产值高且费用较少。
40、过椭圆![]() 的左焦点F1的弦AB,过A,B分别向左准线引垂线,垂足分别为M,N,当线段MN最大时,求直线AB的方程。
的左焦点F1的弦AB,过A,B分别向左准线引垂线,垂足分别为M,N,当线段MN最大时,求直线AB的方程。
解:由已知方程得F1(-4,0),设直线AB方程:y = tg![]() (x+4),代入椭圆方程
(x+4),代入椭圆方程![]() =
=![]() ,当sin
,当sin![]() 时,MN最大
时,MN最大![]() ,
,
此时![]() ∴直线方程为:
∴直线方程为:![]() .
.
41、已知椭圆C:![]() (a>b>0)的长轴两端点为A、B,
(a>b>0)的长轴两端点为A、B,
(1)过焦点F作垂直于长轴的弦PP′,当tg∠APB=![]() 时,求C的离心率;
时,求C的离心率;
(2)如果C上存在一点Q,且∠AQB=1200,求C的离心率的范围。
解:(1)设F为右焦点;P在x轴下方,横坐标为c,则纵坐标为![]() .
.
kPA=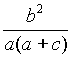 ,kPB=
,kPB=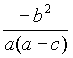 .
.
∴tg∠APB=![]() ,∴
,∴![]() ,∴e=
,∴e=![]() .
.
(2)设θ(x,y),由对称性,不妨设θ在x轴上方,即y>0.
kAQ=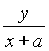 ,kBQ=
,kBQ=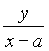 ,∴
,∴![]() =tg∠AQB=
=tg∠AQB=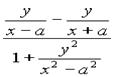 .
.
∴![]() =(x2+y2-a2)+2ay=0.
=(x2+y2-a2)+2ay=0.
此方程与椭圆方程联立,可求出y=0或![]() .由y=0,得Q与A或B重合,舍去.当
.由y=0,得Q与A或B重合,舍去.当![]() 时,由Q在椭圆上半部.
时,由Q在椭圆上半部.
∴![]() ≤b,∴
≤b,∴![]() ,∴e∈
,∴e∈![]() .
.
42、按复利计算利息的一种储蓄,本金为![]() 元,每期利率为
元,每期利率为![]() ,设本利和为
,设本利和为![]() ,存期为
,存期为![]() ,写出本利和
,写出本利和![]() 随存期
随存期![]() 变化的函数式,如果存入本金1000元,每期利率2.25%,试计算5期后的本利和是多少?
变化的函数式,如果存入本金1000元,每期利率2.25%,试计算5期后的本利和是多少?
解:已知本金为![]() 元
元
1期后的本利和为![]() ;
;
2期后的本利和为![]() ;
;
3期后的本利和为![]() ;……
;……
![]() 期后的本利和为
期后的本利和为![]()
将![]() (元),
(元),![]() =2.25%,
=2.25%, ![]() 代入上式得
代入上式得
![]()
由计算器算得![]() (元) 答:复利函数式为
(元) 答:复利函数式为![]() ,
,
5期后的本利和为1117.68元
评述:此题解答的过程体现了解题的思路,再现了探究问题的过程,容易被学生接受。
43、某乡镇现在人均一年占有粮食360千克,如果该乡镇人口平均每年增长1.2%,粮食总产量平均每年增长4%,那么![]() 年后若人均一年占有
年后若人均一年占有![]() 千克粮食,求出函数
千克粮食,求出函数![]() 关于
关于![]() 的解析式。
的解析式。
分析:此题解决的关键在于恰当引入变量,抓准数量关系,并转化成数学表达式,具体解答可以依照例子。
解:设该乡镇现在人口量为M,则该乡镇现在一年的粮食总产量为360M。
经过1年后
该乡镇粮食总产量为360M(1+4%),
人口量为M(1+1.2%)
则人均占有粮食为![]() ;
;
经过2年后:人均占有粮食为![]() ……
……
经过![]() 年后:人均占有粮食
年后:人均占有粮食![]()
即所求函数式为:![]()
评述:这是一个有关平均增长率的问题,如果原来的产值的基础数为N,平均增长率为P,则对于时间![]() 的总产值
的总产值![]() 可以用下面的公式,即
可以用下面的公式,即![]()
解决平均增长率的问题,常用这个函数式。
44、购买一件售价为5000元的商品,采用分期付款方法.每期付款数相同,购买后1个月付款一次,过1个月再付一次,如此下去,到第12次付款后全部付清.如果月利率为0.8%,每月利息按复利算(上月利息要计入下月本金),那么每期应付款多少(精确到1元)?
解:设每期付款x元,根据题意,得到
![]()
所以![]() .
.
由等比数列前n项和的公式得![]()
![]() ,由计算器算得x≈439(元).
,由计算器算得x≈439(元).
答:每期应付款约439元.
解法二:设每期付款x元,第n期后欠款数记作an那么,
第1期后的欠款数为![]()
第2期后的欠款数为![]()
![]()
第3期后的欠款数为![]()
![]() .
.
……
第12期后的欠款数为![]()
![]()
因为第12期全部付清,所以a12=0即
![]() ,
,
![]()
解得 x≈439(元).
答:每期应付款约439元.
