承德市2006年高考模拟试题（二）
文科数学
命题人：廖洪学 审题人：贾增辉
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至3页。第Ⅱ卷3到9页。考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷
注意事项：
1．考生务必将自己的姓名、准考证号填写在第Ⅱ卷上．
2．每小题选出答案后，将所选答案填在第Ⅱ卷的答题卡处，不能答在第I卷上．
参考公式：
如果事件A、B互斥，那么 球是表面积公式
如果事件A、B相互独立，那么 其中R表示球的半径
球的体积公式
如果事件A在一次试验中发生的概率是P，那么 
n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的中四选项中，只有一项是符合题目要求的）
1．已知全集U=R，集合
（ ）
A．{xx<2} B．{xx≤2} C．{x－1<x≤2} D．{x－1≤x<2}
2．设函数
的值等于 （ ）
A．
B．
C．
D．0
3．已知等比数列{an}的前n项和是Sn,S5=2，S10=6，则a16+a17+a18+a19+a20= （ ）
A．8 B．12 C．16 D．24
4．已知
，C为线段AB上距A较近的于个三等分点，D为线段CB上距C
较近的一个三等分点，则用
、
表示
的表达式为 （ ）
A．
B．
C．
D．
5．已知y=f(x)是定义在R上的奇函数，当x>0时，f(x)=x－1，那么不等式f(x)<的解集是 （ ）
A{x0<x<
} B{x－<x<0}
C{x－<x<0或0<x<} D{xx<－或0≤x<}
6．曲线
的一条切线平行于直线y=4x－1，则切点P0的坐标为 （ ）
A．（0，－2）或（1，0） B．（1，0）或（－1，－4）
C．（－1，－4）或（0，－2） D．（1，0）或（2，8）
7．若奇函数
（ ）
A．0 B．1 C． D．5
8．椭圆
的焦点在y轴上，长轴长是短轴长的两倍，则m的值为 （ ）
A．
B． C．2 D．4
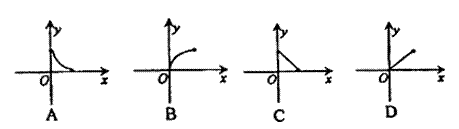
9．一个棱锥被平行于底面的截面截成一个小棱锥和一个棱台（用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫棱台），若小棱锥的体积为y，棱台的体积为x，则y关于x的函数图象大致形状为 （ ）
 |
10．已知
则实数a的取值范围
是 （ ）
A．（－∞，－2）∪（1，+∞） B．（－2，1）
C．
D．
11．设实数
满足条件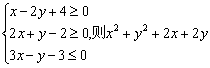
的最大值为 （ ）
A．23 B．25 C．
D．5
12．若对于任意的
，函数
，则称在[a，b]上
可以替代
.若
，则下列函数中可以在[4，16]替代是（ ）
A．
B．
C．
D．
二、填空题（本大题共4小题，每小题4分，共16分.请将答案填在题中的横线上）
13．设
则
=
14．设P是双曲线
上一点，双曲线的一条渐近线方程为
，F1、F2分别是双曲线的左、右焦点.若PF1=3，则点P到双曲线右准线的距离是
.
15．北京市某中学要把9台型号相同的电脑送给西部地区的三所希望学校，每所小学至少得到2台，不同送法的种数共有 种.
16．购买手机的“全球通”卡，使用须付“基本月租费”（每月需交的固定费用）50元，在市内通话时每分钟另收话费0.40元；购买“神州行”卡，使用时不收“基本月租费”，但在市内通话时每分钟话费为0.60元，若某用户每月手机费预算为120元，则它购买
卡才合算.
第Ⅱ卷
注意事项：
1．用钢笔或圆珠笔直接答在试题卷中。2．答卷前将密封线内的项目填写清楚。
一、选择题答题卡：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 选项 |
二、填空题答题卡：
⒔ 。⒕ 。⒖ 。⒗ 。
三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤）
| 得分 | 评卷人 |
|
|
（17）（本大题满分12分）
甲、乙两人独立解出某一道数学题的概率相同，已知该题被甲或乙解出的概率为0.36，求：（1）甲独立解出该题的概率；
（2）甲、乙中有且只有一个解出该题的概率.
| 得分 | 评卷人 |
|
|
（18）（本大题满分12分）
设
是平面上的两个向量，且
互相垂直
（1）求λ的值；
（2）若
的值.
| 得分 | 评卷人 |
|
|
（19）（本大题满分12分）
函数f（x）=1-2a cosx-2sin2x的最小值为g（a）（a∈R）
（1）求g（a）的表达式；（2）若g（a）=，求a及此时f（x）的最大值
| 得分 | 评卷人 |
|
|
（20）（本大题满分12分）
|
（1）求CD的长；
（2）求证：AF⊥BD；
（3）求平面ADF与平面ABC
所成的较小的二面角的大小.
| 得分 | 评卷人 |
|
|
（21）（本大题满分12分）
已知数列
的前n项和为Sn，且
（1）求证：
为等差数列；
（2）求满足
的自然数n的集合.
| 得分 | 评卷人 |
|
|
（22）（本大题满分14分）
已知椭圆
两焦点分别为F1、F2，P是椭圆在第一象限弧上一点，并满足
=1，过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点，
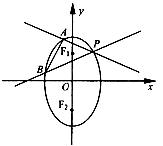（1）求P点坐标；
（2）求证直线AB的斜率为定值；
（3）求△PAB面积的最大值.
承德市2006年高考模拟试卷（二） 文科数学
参考答案及评分标准
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | A | D | B | C | A | C | C | A | C |
二、填空题
13．1 14．
15．10 16．神州行
三、解答题：
17．解：（1）设甲、乙独立解出该题的概率为x，则甲、乙均未解出该题的概率为
，该题被甲或乙解出的概率为1－=0.36，解得x=0.2，故甲独立解出该题的概率为0.2. ……………………（6分）
（2）0.2×0.8+0.8×0.2=0.32，即甲、乙中有且只有一个解出该题的概率为0.32 ……12分
18.解：
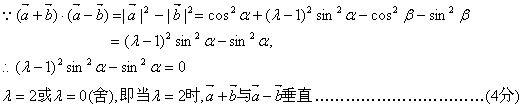
（2）当垂直时，
，则
|
|
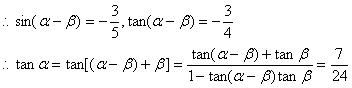
19．解：（1）f（x）=1-2a cosx-2sin2x=2 cos2x-2a cosx -2a-1
设h（t）=2t2-2a t -2a-1=2（t-
）2 -
-2a-1，t=
cosx ∈
。
①当<-1时，即a<-2时，g（a）=h（t）min= h（-1）=1。
|
≤1时，即-2≤a≤2时，g（a）=h（t）min= h（）=--2a-1。
③当>1时，即a>2时，g（a）=h（t）min= h（1）=1-4 a。
（2）当a<-2时，g（a）=1≠；
当a>2时，g（a）=h（t）min= h（1）=1-4 a=，得a=
；
|
-2a-1=，则a= -3（舍）或a= -1。
|
）2 +。
当cosx= 1时，f（x）有最大值为5。
20．方法一：（1）取AB中点G，连FG、CG，则FG//AE，又AE和CD都垂直平面ABC，
所以AE//CD，所以FG//CD，所以F、G、C、D四点共面.又平面
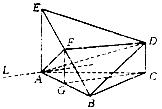FGCD∩平面ABC=CG，DF//平面ABC，所以DF//CG，所以四边形FGCD是平行四边形，所以CD=FG=AE=1.………………（4分）
（2）直角三角形ABE中，AE=AB，F是BE的中点，
所以AF⊥BE，又△ABC中，AC=BC，G是AB中
点，所以CG⊥AB，又AE垂直于平面ABC，所以
AE⊥CG，又AE∩AB=A，所以CG⊥面ABE.因为
DF//CG，所以DF⊥面ABE，AF⊥BE，由三垂线定
理得AF⊥BD.……（8分）
（3）设面ADF∩面ABC=L，因为DF//平面ABC，所以DF//L，又DF⊥面ABE，所以L⊥面ABE，所以L⊥AF，L⊥AB，所以∠EAB即为二面角的平面角.直角三角形ABE中，易得∠FAB=45°，所以平面ADF与平面ABC所形成的较小的二面角为45°…………（12分
方法二：取AB的中点G，∵AB=BC，∴CG⊥AB
又∵AE⊥平面ABC，∴GF⊥平面ABC以G
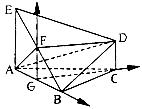为原点，GB、GC、GF所在的直线为x, y,
z建
立空间直角坐标系，则A（－1，0，0）B（1，0，0），
E（－1，0，2）F（0，0，1），设C（0，t，0）
∵DF//平面ABC，则D（0，t，1）
∴
即CD的长为1…………………………（4分）
（2）
=（1，0，1），
=（－1，t，1）∵·=－1+1=0，∴AF⊥BD（8分）
（3）∵=（1，0，1），
=（0，t，0），设
=(x, y, z)是平面ADF的一个法向量，
∴
GF⊥平面ABC，则
=（0，0，1）是平面ABC的一个法向量，设平面ADF与平面ABC所成的二面角（锐角）为θ，则
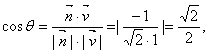所以θ=45°
即：平面ADF与平面ABC所成的较小的二面角为45°……………………（12分）
21． （1）证明：
∴
∴是公差为－1的等差数列. ………………6分
（2）解：
∴
∴
………………8分
解得 
∴满足的自然数n的集合为{3，4，5，7}. …………12分
22．解：（1）由题可得F1(0, 
), F2(0, －), 设P(x0, y0)(x0>0,
y0>0)
则
在曲线上，则
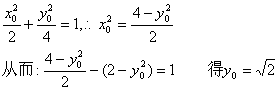
则点P的坐标为（1，）………………………………（2分）
（2）由题意知，两直线PA、PB的斜率必存在，设PB的斜率为k(k>0)
则BP的直线方程为：y－=k(x－1)
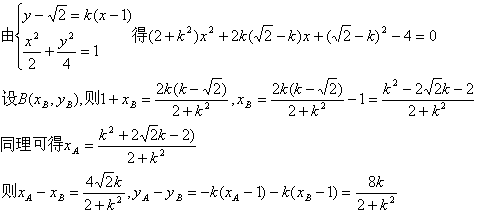
所以：AB的斜率
为定值…………………………（8分）
（3）设AB的直线方程：
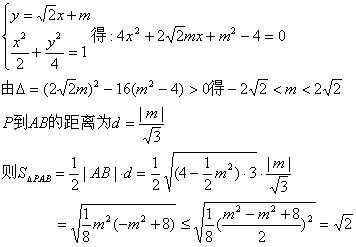
当且仅当m=±2∈（－2，2）取等号
∴三角形PAB面积的最大值为………………………………（14分）