高考数学中档题精选（1）

1.　  已知函数f(x)=+cos².

(1) 求函数f(x)的最小正周期和值域；

(2)  求函数f(x)的单调递增区间.

解：(1) y=sin 

　　　　  =

　　　　  ==

∴T=,值域y∈[].

(2)由2kπ-≤3x+≤2kπ+,k∈Z.得:(k∈Z).

2.　  设数列{a_n}的前n项和为S_n,已知a₁=1,S_n=na_n-2n(n-1)(n∈N)

(1)求证数列{a_n}为等差数列，并写出其通项公式；

(2)是否存在非零常数p、q使数列{}是等差数列？若存在，试求出p、q应满足的关系式，若不存在，请说明理由.

解：（1）当n≥2时，a_n=S_n-S_n-1=na_n-(n-1)a_n-1-4(n-1)，即a_n-a_n-1=4(n≥2)

∴{a_n}为等差数列.∵a₁=1,公差d=4,∴a_n=4n-3.

（2）若{}是等差数列，则对一切n∈N，都有＝An+B,

即S_n=(An+B)(pn+q),又S_n==2n²-n,∴2n²-n=Apn²+(Aq+Bp)n+Bq

要使上式恒成立，当且仅当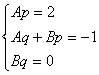，∵q≠0,∴B＝0，∴=-2,

即：p+2q=0.

3.　  已知正三棱锥A-BCD的边长为a，E、F分别为AB、BC的中点，且AC⊥DE.

（Ⅰ）求此正三棱锥的体积；

（Ⅱ）求二面角E-FD-B的正弦值.

解：（Ⅰ）作AO⊥平面BCD于O,由正三棱锥的性质

可知O为底面中心，连CO,则CO⊥BD,由三垂线定理

知AC⊥BD，又AC⊥ED,∴AC⊥平面ABD,∴AC⊥AD,

AB⊥AC,AB⊥AD.在Rt△ACD中，由AC²+AD²=2AC²=a²

可得：AC=AD=AB=.

∴V=V_B-ACD=.

（Ⅱ）过E作EG⊥平面BCD于G，过G作GH⊥FD于H，连EH，由三垂线定理知EH⊥FD,即∠EHG为二面角E-FD-B的平面角.

∵EG＝AO 而AO＝,∴EG=.

又∵ED＝∵EF∥AC，∴EF⊥DE.∴在Rt△FED中，EH＝∴在Rt△EGH中，sin∠EHG＝

*选做题：定义在区间（－1,1）上的函数f(x)满足：①对任意x、y∈（－1,1）都有f(x)+f(y)=f();②当x∈（－1,0）时，f(x)>0.

（Ⅰ）求证：f(x)为奇函数；

（Ⅱ）试解不等式f(x)+f(x-1)>f().

解：（Ⅰ）令x=y=0,则f(0)+f(0)=f(0),∴f(0)=0.

又令x∈（－1,1），则-x∈（－1,1），而f(x)+f(-x)=

∴f(-x)=-f(x),即f(x)在（－1,1）上是奇函数.

（Ⅱ）令－1<x₁<x₂<1,则x₁-x₂<0,1-x₁x₂>0,

于是f(x₁)-f(x₂)=f(x₁)+f(-x₂)=f()>0,即f(x₁)>f(x₂),所以f(x)在定义域上为减函数.从而f(x)+f(x-1)>f()等价与不等式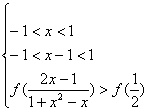

高考数学中档题精选（2）

1. 已知z是复数，且arg(z-i)=,z=.求复数z.

解法1.设复数z-i的模为r(r>0),则z-i=r(cos+isin),

∴，

解得r=,z=1+2i.

解法2.设z=x+yi,则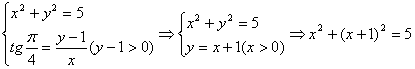

解得x=1或－2(舍去)，所以z=1+2i.

解法3.设则

解得：

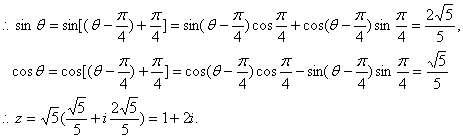
2. 已知f(x)=sin²x-2(a-1)sinxcosx+5cos²x+2-a,若对于任意的实数x恒有f(x)≤6成立，求a的取值范围.

解：f(x)=(1-a)sin2x+2cos2x+5-a=sin(2x+ψ)＋5-a.(ψ为一定角，大小与a有关).

∵x∈R,∴[f(x)]_max=5-a+,[f(x)]_min=5-a-.

由f(x)≤6,得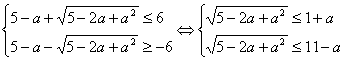

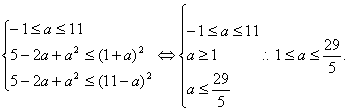
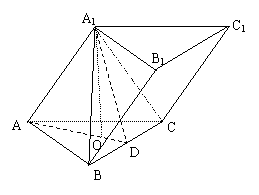3.斜三棱柱ABC-A₁B₁C₁的底面是边长为2的正三角形，顶点A₁在底面的射影O是△ABC的中心，异面直线AB与CC₁所成的角为45°.

(1)求证：AA₁⊥平面A₁BC；

(2)求二面角A₁－BC-A的平面角的正弦值；

(3)求这个斜三棱柱的体积.

(1)由已知可得A₁-ABC为正三棱锥，∠A₁AB=45°

∴∠AA₁B=∠AA₁C=90°即AA₁⊥A₁B,AA₁⊥A₁C

∴AA₁⊥平面A₁BC

(2)连AO并延长交BC于D,则AD⊥BC，连A₁D,

则∠ADA₁为所求的角。由已知可得 AD＝Absin60°＝,

AA₁=Absin45°=,∴sin∠ADA₁=

(3)在Rt△AA₁D中，A₁D=∴A₁O=

∴V_柱＝S_△ABC·A₁O=·4·sin60°·.

*选做题：已知函数f(x)=log_a(ax-)(a>0,a≠1)

(1)求函数f(x)的定义域；

(2)若函数y=f(x)是增函数，求a的取值范围.

解：（1）由ax->0　得x>.即f(x)的定义域为（，＋∞）

(2)设x₁>x₂>,则a

∴(ax₁-)-(ax₂-)=(>0,

∴ax₁-> ax₂-∵f(x)是增函数，∴f(x₁)>f(x₂)∴a>1.

高考数学中档题精选（3）

1.　　　已知△ABC的外接圆直径为1,且角A、B、C成等差数列，若角A、B、C所对的边长分别为a、b、c，求a²+c²的取值范围.

解法1：由A、B、C成等差数列，得2B=A+C，又A+B+C=180°∴B＝60°

设A=60°+α，B=60°－α，由0°<A,C<120°得－60°<α<60°,

由正弦定理得：a=2RsinA=sinA,c=2RsinC=sinC

则 a²+c² =sin²A+sin²C=

=1－[cos(120°+2α)+cos(120°－2α)]

=1+cos2α

∵－60°<α<60°-120°<2α<120°∴－<cos2α≤1　∴a²+c²∈().

解法2：由正弦定理得：b=2RsinB=sinB=

由余弦定理得：b²=a²+c²-2accosB,∴a²+c²= ∵a>0,c>0,∴a²+c²> ,

又∵ac≤∴a²＋c²≤　即a²+c²≤.

∴<a²+c²≤

2.已知等差数列{a_n}中，a₁=1,公差d≠0,若S_n=a₁+a₂+……+a_n，S^'_2n=a_n+1+a_n+2+……+a_3n，且S_n与S'_2n的比与n无关.

(1)　 求等差数列{a_n}的通项公式；

(2)　 求的值.

解：（1）设

即2－d+nd=p(8nd+4－2d),所以n(8pd－d)+4p－2pd+d－2=0与n无关，且d≠0，

则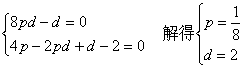，即等差数列的通项公式是a_n=2n－1.

（2）

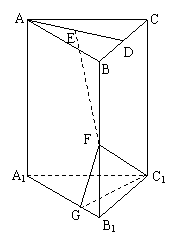3.如图，已知直三棱柱ABC－A₁B₁C₁中，AB=AC，D为

BC中点，F为BB₁上一点，BF=BC=2,FB₁=1.

(1)　 求证：AD⊥平面BB₁C₁C;

(2)　 若E为AD上不同于A、D的任一点，求证：EF⊥FC₁;

(3)　 若A₁B₁=3,求FC₁与平面AA₁B₁B所成角的大小.

解：如图，（1）∵AB=AC且D为BC中点，∴AD⊥BC

∵ABC－A₁B₁C₁是直三棱柱，∴平面ABC⊥平面BB₁C₁C

∴AD⊥平面BB₁C₁C.

(2)连结DF,DC₁,由已知可求得DF=,FC­₁=DC₁=,

DF²+FC₁²=DC₁²,∴∠DFC₁=90°，即DF⊥CF₁，由三垂线

定理知EF⊥FC₁.

(3)作C₁G⊥A₁B₁, 垂足为G,则C₁G⊥平面AA₁B₁B,∴∠C₁FG即为所求的角.

在Rt△ABD中，可求得AD=2.由C₁G·A₁B₁=AD·BC

得 C₁G = ∴sin∠C₁FG＝

∴∠C₁FG＝arcsin.

*选做题：设函数f(x)的定义域为R，对于任意实数x、y，总有f(x+y)=f(x)f(y)，且当x>0时，0<f(x)<1.

(1)　 证明：f(0)=1，且x<0时，f(x)>1；

(2)　 证明：f(x)在R上单调递减；

(3)　 设M={(x,y)f(x²)f(y²)>f(1)}，N={(x,y)f(ax-y+2)=1,a∈R}，若M∩N=φ，试确定a的取值范围.

证明：(1)在f(x+y)=f(x)f(y)中，令x=1,y=0,得f(1)=f(1)f(0)，因为0<f(1)<1,所以f(0)=1.

取y＝－x>0,则f(x－x)=f(x)f(－x)=1,即f(x)=,∵0<f(－x)<1,∴f(x)>1.

(2)设x₁<x₂，则x₂－x₁>0，于是，0<f(x₂－x₁)<1,f(x₁)>0,

∴f(x₂)－f(x₁)=f[(x₂－x₁)+x₁]－f(x₁)=f(x₂－x₁)f(x₁)－f(x₁)=f(x₁)[f(x₂－x₁)－1]<0,

∴f(x)在R上单调递减.

(3)解：由f(x²)f(y²)>f(1)，得f(x²+y²)>f(1)，即x²+y²<1；

由f(ax－y+2)=1=f(0)，得ax－y+2=0

由若M∩N=φ，得，解得－≤a≤.