高考数学第一轮总复习试卷
复 数
第I卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
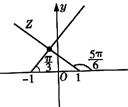
1.已知复数z-1的辐角为![]() ,z+1的辐角为
,z+1的辐角为![]() ,则复数z是( )
,则复数z是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.把复数-1+i所对应的向量绕原点按顺时针方向旋转120°,所得向量对应的复数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.把复数1+i对应的点向右平移一个单位,再向下平移一个单位得到点A,把所得向量![]() 按逆时针方向旋转120°,得到向量
按逆时针方向旋转120°,得到向量![]() ,则B点对应复数为( )
,则B点对应复数为( )
A.![]() B.0
B.0
C.![]() D.
D.![]()
4.已知![]() 是方程
是方程![]() 的两根,且
的两根,且![]() ,则
,则![]() 等于( )
等于( )
A.1+i B.1-i C.-i D.i
5.已知方程![]() 有实根b,且z=a+bi,则z等于( )
有实根b,且z=a+bi,则z等于( )
A.2-2i B.2+2i C.-2+2i D.-2-2i
6.已知z=1+i,复数![]() ,那么w的三角形式为( )
,那么w的三角形式为( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
7.已知复数2-i的辐角主值是θ,则![]() 的辐角主值是( )
的辐角主值是( )
A.![]() B.2π-θ C.
B.2π-θ C.![]() D.
D.![]()
8.若![]() ,则复数
,则复数![]() 的辐角主值是( )
的辐角主值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.复数![]() 在复平面上对应的点分别是A、B,O为坐标原点,若
在复平面上对应的点分别是A、B,O为坐标原点,若![]() ,
,![]() ,则△AOB的面积为( )
,则△AOB的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
10.如果复数z适合z+2+2i=z,那么z-1+i的最小值为( )
A.4
B.![]() C.2
D.
C.2
D.![]()
11.已知复数z=x+yi(x,y∈R,![]() )满足z-1=x,那么复数Z在复平面上的对应点(x,y)的轨迹是( )
)满足z-1=x,那么复数Z在复平面上的对应点(x,y)的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
12.已知z≤1,则z-2i的辐角主值的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第II卷 (非选择题 共90分)
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中横线上)
13.设![]() ,则
,则![]() 。
。
14.若z=sin50°+icos50°,则![]() 。
。
15.虚线z满足![]() 是实数,且
是实数,且![]() ,则z=______________。
,则z=______________。
16.关于x的实系数方程![]() 的两虚根分别为
的两虚根分别为![]() ,且
,且![]() ,则a=________________。
,则a=________________。
三、解答题(本大题共6个小题,共74分,解答应写出必要文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知z∈C,![]()
(1)求z的最小值;
(2)若![]() ,求z。
,求z。
18.(本小题满分12分)
在△ABC中,∠A,∠B,∠C的对边分别为a,b,c。若![]() 。
。
(1)求cos(B-C)的值;
(2)设复数z=sin(B+C)-icos(B-C),求![]() 的值。
的值。
19.(本小题满分12分)
已知三边都不相等的三角形ABC的三内角A、B、C满足sinAcosB+sinB=sinAcosC+sinC,设复数![]() ,求
,求![]() 的值。
的值。
20.(本小题满分12分)
已知![]() ,求
,求![]() 。
。
21.(本小题满分12分)
设z是虚数,![]() 是实数,且-1<w<2。
是实数,且-1<w<2。
①求z的值及z的实部的取值范围;
②设![]() ,求证u为纯虚数;
,求证u为纯虚数;
③求![]() 的最小值。
的最小值。
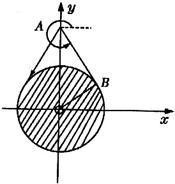
22.(本小题满分14分)
复平面上点A,B对应的复数分别为![]() ,点P对应的复数为z,
,点P对应的复数为z,![]() 的辐角主值为
的辐角主值为![]() ,当P在以原点为圆心,1为半径的上半圆周(不包括两个端点)上运动时,求
,当P在以原点为圆心,1为半径的上半圆周(不包括两个端点)上运动时,求![]() 的最小值。
的最小值。
参考答案
一、选择题
1.B 数形结合
2.C ![]()
3.A ![]() ,
,![]()
4.D ![]() ,
,![]() ,
,![]()
5.A ![]() 得
得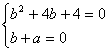
∴![]()
6.D
![]()
7.C ![]() 数形结合
数形结合![]()
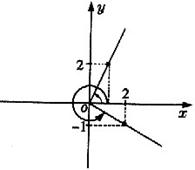
8.C ![]()
又![]() ∴
∴![]() ∴
∴![]()
9.B ![]()
10.D 数形结合![]() z对应点的轨迹为(0,0)与(-2,-2)线段的中垂线,
z对应点的轨迹为(0,0)与(-2,-2)线段的中垂线,![]() 表示乙到(1,-1)距离,最小值为
表示乙到(1,-1)距离,最小值为![]()
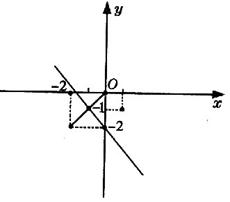
11.D ![]() ∴
∴![]()
即![]()
12.C 数形结合![]() 表示单位圆内部,A(0,2),AB为圆切线,
表示单位圆内部,A(0,2),AB为圆切线,![]()
∴ ![]() ,最大辐角为
,最大辐角为![]()
二、填空题
13.1 14.![]() 15.±i 16.
15.±i 16.![]()
提示:
13.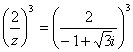
14.
![]()
![]()
15.设![]()
![]()
则 ![]() ,则
,则![]() ①
①
又 ![]() ∴
∴![]() ②
②
由①、②知 a=0,![]()
16.![]() ,
,![]()
设![]() ,则
,则![]() (
(![]() 且
且![]() )
)
则 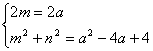
又 ![]() ∴
∴![]() 或
或![]()
∴ ![]() ∴
∴![]() 或
或![]()
又![]()
∴ a<1,故![]() .
.
三、解答题
17.(1)设![]() 由已知得 a=b+1 ①
由已知得 a=b+1 ①
∵ ![]()
∴![]()
(2)∵![]()
∴![]() 且a>0与①式联立得
且a>0与①式联立得![]() ,
,![]()
∴![]()
18.(1)由![]() 得
得![]()
∴![]() ,
,![]()
由![]() 得
得![]()
∴ ![]()
∴![]()
(2)∵
![]() ,
,![]()
∴![]() ∴
∴![]() ∴
∴![]()
19.解:∵ ![]()
∴![]()
得![]()
∵ ![]()
∴![]() ,
,![]() 。
。
又![]() ,
,
∴![]() ,
,![]() 。
。
上式化简为![]()
∴![]()
![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
20.设![]() ,
,![]() (∵
(∵![]() )
)
∴![]() ,
,![]()
∴![]()
∴![]()
![]()
∴![]()
21.(1)设![]()
![]()
由已知![]() 为实数,∴
为实数,∴![]() ,
,
又b≠0,∴![]() ,∴
,∴![]()
∴![]() ,又
,又![]() 。
。
∴z的实部取值范围为![]()
(2)![]()
∴b≠0,∴得证
(3)![]()
当a=0时取“=”号
22.由已知,设![]()
![]()
∴ 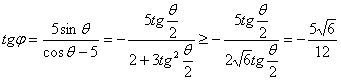
又![]() 。
。 ![]()
∴![]() 的最小值是
的最小值是![]()