2004-2005届高考数学仿真试题（三）（广东）

命题：廖美东　　　　　　　　  考试时间：2005-4-9

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.

注意事项：

1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.

2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.

3.考试结束，监考人将本试卷和答题卡一并收回.

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　  正棱锥、圆锥的侧面积公式

P（A+B）=P（A）+P（B）　　　　　　　　　　　 

如果事件A、B相互独立，那么　　　　　　　　　　　  其中c表示底面周长，l表示斜

P（AB）=P（A）P（B）　　　　　　　　　　　  高或母线长

如果事件A在一次试验中发生的概率是　　　　　　　　 球的体积公式

P，那么n次独立重复试验中恰好发生k次的概率　　　　

　　　　　　　　　　　　　　  其中R表示球的半径

第Ⅰ卷（选择题　共50分）

一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.已知集合P=｛(x,y)｜y=,Q=｛(x,y)｜y=a^x+,且P∩Q=,那么k的取值范围是

A.(－∞,1)　　　　　　　　　　B.(－∞,　　　　　　　　　　C.(1,+∞)　　　　　　　　　　　　　　D.(－∞,+∞)

2.已知sinθ=－,θ∈(－,0),则cos(θ－)的值为

A.－　　　　　　　　　　B.　　　　　　　　　　　　C.－　　　　　　　　　D.

3.双曲线kx²+5y²=5的一个焦点是（0，2），则k等于

A.　　　　　　　　　　　　　　B.－　　　　　　　　　　　　 C.　　　　　　　　　　　　D.－

4.已知a=(2,1),b=(x,1),且a+b与2a－b平行，则x等于

A.10　　　　　　　　　　　　　　　　　 B.－10　　　　　　　　　　　　 C.2　　　　　　　　　　　　　　　D.－2

5.数列1,3,5,7,…,(2n－1)+的前n项之和为S_n，则S_n等于

A.n²+1－　　　　　　　　B.2n²－n+1－　　　　 C.n²+1－　　　　　　　D.n²－n+1－

6.已知非负实数x,y满足2x+3y－8≤0且3x+2y－7≤0,则x+y的最大值是

A.　　　　　　　　　　　　　　B.　　　　　　　　　　　　　　　　　 C.3　　　　　　　　　　　　　　　D.2

7.一个凸多面体的面数为8，各面多边形的内角总和为16π，则它的棱数为

A.24　　　　　　　　　　　　　　　　　 B.22　　　　　　　　　　　　　　 C.18　　　　　　　　　　　　　　　　　 D.16

8.若直线x+2y+m=0按向量a=(－1,－2)平移后与圆C：x²+y²+2x－4y=0相切，则实数m的值等于

A.3或13　　　　　　　　　　　B.3或－13　　　　　　　　　 C.－3或7　　　　　　　　　　D.－3或－13

9.设F₁、F₂为椭圆+y²=1的两个焦点，P在椭圆上，当△F₁PF₂面积为1时，·的值为

A.0　　　　　　　　　　　　　　　B.1　　　　　　　　　　　　　　　C.2　　　　　　　　　　　　　　　D.

10.显示屏有一排7个小孔，每个小孔可显示0或1，若每次显示其中3个孔，但相邻的两孔不能同时显示，则该显示屏能显示信号的种数共有

A.10　　　　　　　　　　　　　　　　　 B.48　　　　　　　　　　　　　　 C.60　　　　　　　　　　　　　　　　　 D.80

第Ⅱ卷(非选择题  共100分)

二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中横线上）

11.锐角△ABC中，若B=2A，则的取值范围是___________.

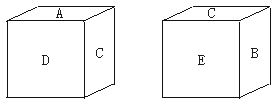12.一个正方体的六个面上分别标有字母A、B、C、D、E、F，右图是此正方体的两种不同放置，则与D面相对的面上的字母是_________.

13.随机抽取甲、乙两位同学在平时数学测验中的5次成绩如下：

甲	88	92	85	94	91
乙	92	87	85	86	90

从以上数据分析，甲、乙两位同学数学成绩较稳定的是_________同学.

14.给出以下命题：

①已知向量，，满足条件++=0，且｜｜=｜｜=｜｜=1，则△P₁P₂P₃为正三角形；

②已知a＞b＞c,若不等式恒成立，则k∈(0,2);

③曲线y=x³在点(1,)处切线与直线x+y－3=0垂直；

④若平面α⊥平面γ,平面β∥平面γ，则α∥β.

其中正确命题的序号是___________.

三、解答题(本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤)

15.（本小题满分12分）

甲、乙两名篮球运动员，投篮的命中率分别为0.7与0.8.

(1)如果每人投篮一次，求甲、乙两人至少有一人进球的概率；

(2)如果每人投篮三次，求甲投进2球且乙投进1球的概率.

16.(本小题满分12分)

已知向量a=(cos,sin),b=(cos,－sin),且x∈［,］.

(1)求a·b及｜a+b｜;

(2)求函数f(x)=a·b－｜a+b｜的最小值.

17.（本小题满分13分）

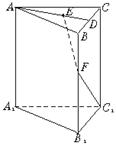
如图，已知直三棱柱ABC—A₁B₁C₁，AB=AC，F为BB₁上一点，D为BC的中点，且BF=2BD.

（1）当为何值时，对于AD上任意一点总有EF⊥FC₁;

(2)若A₁B₁=3，C₁F与平面AA₁B₁B所成角的正弦值为,当在（1）所给的值时，求三棱柱的体积.

18.（本小题满分13分）

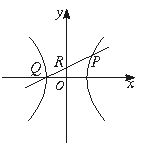
一条斜率为1的直线l与离心率为的双曲线=1(a＞0,b＞0)交于P、Q两点，直线l与y轴交于R点，且·=－3,=3,求直线与双曲线的方程.

19.(本小题满分14分)

已知点B₁（1,y₁）,B₂(2,y₂),…,B_n(n,y_n),…(n∈N^*)顺次为直线y=+上的点，点A₁（x₁,0），A₂(x₂,0),…,A_n(x_n,0)顺次为x轴上的点，其中x₁=a(0＜a＜1).对于任意n∈N^*，点A_n、B_n、A_n+1构成以B_n为顶点的等腰三角形.

(1)求数列｛y_n｝的通项公式，并证明它为等差数列；

（2）求证：x_n+2－x_n是常数，并求数列｛x_n｝的通项公式.

(3)上述等腰△A_nB_nA_n+1中是否可能存在直角三角形，若可能，求出此时a的值；若不可能，请说明理由.

20.（本小题满分16分）

已知函数f(x)=x³+(b－1)x²+cx(b、c为常数).

(1)若f(x)在x=1和x=3处取得极值，试求b、c的值.

(2)若f(x)在x∈(－∞,x₁),(x₂,+∞)上单调递增且在x∈(x₁,x₂)上单调递减，又满足x₂－x₁＞1,求证：b²＞2(b+2c);

(3)在（2）的条件下，若t＜x₁,试比较t²+bt+c与x₁的大小，并加以证明.

2004-2005届高考数学仿真试题（三）（广东）

参考答案

一1.B  2.A　3.B　4.C  5.A　6.C　7.D  8.D　9.A　10.D

二  11.(,)　12.B　13.乙　14.①③

三15.设甲投中的事件记为A，乙投中的事件记为B，

（1）所求事件的概率为：

P=P(A·)+P(·B)+P(A·B)

=0.7×0.2+0.3×0.8+0.7×0.8

=0.94.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

（2）所求事件的概率为：

P=C0.7²×0.3×C0.8×0.2²

=0.042336.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

16.（1）a·b=coscos+sin(－sin)

=coscos－sinsin

=cos(+)

=cos2x.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分

a+b=(cos+cos,sin－sin)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3分

∴｜a+b｜===

=2｜cosx｜.　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　5分

∵x∈［,］,∴｜a+b｜=－2cosx.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

（2）f(x)=a·b－｜a+b｜=cos2x－(－2cosx)=cos2x+2cosx=2cos²x+2cosx－1

=2(cosx+)²－.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

∵x∈［,］,∴－1≤cosx≤0,

∴当cosx=－时，［f(x)］_min=－.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

17.（1）由三垂线定理得C₁F⊥DF,易证Rt△BDF≌Rt△B₁FC₁,

∴B₁F=BD=BF,∴=2.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

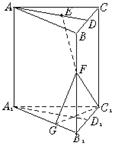（2）在平面A₁B₁C₁中，过C₁作C₁G⊥A₁B₁于G，连FG，

易证∠C₁FG就是C₁F与侧面AA₁B₁B所成的角，　　　　　　　　8分

则有=,C₁G=C₁F,

△A₁B₁C₁中，取B₁C₁的中点D₁，连A₁D₁，设B₁F=x,由C₁G·A₁B=B₁C·A₁D₁,

解得x=1,∴BB₁=3,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

∴V=B₁G·A₁D₁·BB₁=6.　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 13分

18.∵e=,∴b=2a²,

∴双曲线方程可化为2x²－y²=2a²,　　　　　　　　　　　　　　　　 2分

设直线方程为y=x+m,

由得x²－2mx－m²－2a²=0.　　　　　　　　　4分

∵Δ=4m²+4(m²+2a²)＞0,

∴直线一定与双曲线相交，　　　　　　　　　　　　　　　　　　　　　6分

设P(x₁,y₁),Q(x₂,y₂),

则x₁+x₂=2m,x₁x₂=－m²－2a²,

∵=3,

∴x_R=,x₁=－3x₂,

∴x₂=－m,－3x₂²=－m²－2a²,

消去x₂得，m²=a²,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

·=x₁x₂+y₁y₂=x₁x₂+(x₁+m)(x₂+m)

=2x₁x₂+m(x₁+x₂)+m²

=m²－4a²

=－3,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 10分

∴m=±1,a²=1,b²=2,直线方程为y=x±1,

双曲线方程为x²－=1.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 13分

19.（1）y_n=n+,y_n+1－y_n=,

∴数列｛y_n｝是等差数列，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

（2）由题意得，=n,

∴x_n+x_n+1=2n,　　　　　　　　　　　　　　 ①

x_n+1+x_n+2=2(n+1),　　　　　　　　　　　　②

①、②相减，得x_n+2－x_n=2,

∴x₁,x₃,x₅,…,x_2n－1,…成等差数列；

x₂,x₄,x₆,…,x_2n,…成等差数列，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分

∴x_2n－1=x₁+2(n－1)=2n+a－2,

x_2n=x₂+(n－1)·2=(2－a)+(n－1)·2

=2n－a,

∴x_n=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　7分

（3）当n为奇数时，A_n(n+a－1,0),A_n+1 (n+1－a,0)

所以｜A_nA_n+1｜=2(1－a);

当n为偶数时，A_n(n－a,0),A_n+1 (n+a,0),

所以｜A_nA_n－1｜=2a,

作B_nC_n⊥x轴于C_n,则｜B_nC_n｜=n+.

要使等腰三角形A_nB_nA_n+1为直角三角形，必须且只须｜A_nA_n+1｜=2｜B_nC_n｜.　 　 12分

所以，当n为奇数时，有2(1－a)=2(n+),

即12a=11－3n,(*)

当n=1时，a=;

当n=3时，a=;

当n≥5时，方程(*)无解.

当n为偶数时，12a=3n+1,同理可求得a=.

综上，当a=,或a=或a=时，存在直角三角形.　　　　　　　　　　　　　　　　　　　　 16分

20.（1）f′(x)=x²+(b－1)x+c,

由题意得，1和3是方程x²+(b－1)x+c=0的两根，

∴　解得　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

（2）由题得，

当x∈(－∞,x₁),(x₂,+∞)时，f′(x)＞0

x∈(x₁,x₂)时，f′(x)＜0,

∴x₁,x₂是方程x²+(b－1)x+c=0的两根，

则x₁+x₂=1－b,x₁x₂=c,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　7分

∴b²－2(b+2c)=b²－2b－4c

=［1－(x₁+x₂)］²－2［1－(x₁+x₂)］－4x₁x₂

=(x₁+x₂)²－4x₁x₂－1

=（x₂－x₁)²－1,

∵x₂－x₁＞1,

∴(x₂－x₁)²－1＞0,

∴b²＞2(b+2c).　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　9分

（3）在（2）的条件下，由上一问知

x²+(b－1)x+c=(x－x₁)(x－x₂),

即x²+bx+c=(x－x₁)(x－x₂)+x,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

所以，t²+bt+c－x₁=(t－x₁)(t－x₂)+t－x₁,

=(t－x₁)(t+1－x₂)，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分

∵x₂＞1+x₁＞1+t,∴t+1－x₂＜0,

又0＜t＜x₁,∴t－x₁＜0,

∴(t－x₁)(t+1－x₂)＞0,

即t²+bt+c＞x₁.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 16分