2004-2005届高考数学仿真试题(四)(广东)
命题:廖美东 考试时间:2005-4-13
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么 其中c表示底面周长,l表示斜
P(AB)=P(A)P(B) 高或母线长
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k次的概率
![]()
![]() 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.命题p:a2+b2<0(a,b∈R);命题q:a2+b2≥0(a,b∈R),下列结论正确的是
A.“p或q”为真 B.“p且q”为真
C.“非p”为假 D.“非q”为真
2.已知向量a=(cos75°,sin75°),b=(cos15°,sin15°),那么|a-b|的值是
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
3.正项等比数列{an}满足:a2·a4=1,S3=13,bn=log3an,则数列{bn}的前10项的和是
A.65 B.-65 C.25 D.-25
4.空间四边形四条边所在的直线中,互相垂直的直线最多有
A.2对 B.3对 C.4对 D.5对
5.P为椭圆![]() =1上一点,F1、F2为焦点,如果∠PF1F2=75°,∠PF2F1=15°,则椭圆的离心率为
=1上一点,F1、F2为焦点,如果∠PF1F2=75°,∠PF2F1=15°,则椭圆的离心率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.有下面四个命题,其中正确命题的序号是
①“直线a、b为异面直线”的充分而不必要条件是“直线a、b不相交”;
②“直线l⊥平面α内所有直线”的充要条件是“l⊥平面α”;
③“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
④“直线a∥平面α”的必要而不充分条件是“直线a平行于α内的一条直线.”
A.①③ B.②③ C.②④ D.③④
7.如果a1、a2、a3、a4、a5、a6的平均数(期望)为3,那么2(a1-3)、2(a2-3)、2(a3-3)、2(a4-3)、2(a5-3)、2(a6-3)的平均数(期望)是
A.0 B.3 C.6 D.12
8.如果函数y=log2|ax-1|(a≠0)的图象的对称轴方程是x=-2,那么a等于
A.![]() B.-
B.-![]() C.2 D.-2
C.2 D.-2
9.若f(x)=ax3+3x2+2,且f′(-1)=4,则a等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知抛物线y=ax2的焦点为F,准线l与对称轴交于点R,过抛物线上一点P(1,2)作PQ⊥l,垂足为Q,则梯形PQRF的面积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
11.已知x、y满足线性约束条件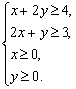 则线性目标函数z=3x+2y的最小值是_________.
则线性目标函数z=3x+2y的最小值是_________.
12.(1-x+x2)3(1-2x2)4=a0+a1x+a2x2+…+a14x14,则a1+a3+a5+…+a11+a13=___________.
13.有三个球和一个正方体,第一个球与正方体各个面相内切,第二个球与正方体各条棱相切,第三个球过正方体各顶点,则这三个球的面积之比为___________.
14.设函数f(x)=sin(wx+![]() )(w>0,-
)(w>0,-![]() <
<![]() <
<![]() ,给出以下四个结论:
,给出以下四个结论:
①它的周期为π;②它的图象关于直线x=![]() 对称;③它的图象关于点(
对称;③它的图象关于点(![]() ,0)对称; ④在区间(-
,0)对称; ④在区间(-![]() ,0)上是增函数.
,0)上是增函数.
以其中两个论断为条件,另两个论断作结论写出你认为正确的一个命题:
________________________________________________________________________.
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分12分)
沿某大街在甲、乙、丙三个地方设有红、绿交通信号灯,汽车在甲、乙、丙三个地方通过(绿灯亮通过)的概率分别为![]() ,
,![]() ,
,![]() ,对于在该大街上行驶的汽车,
,对于在该大街上行驶的汽车,
求:(1)在三个地方都不停车的概率;
(2)在三个地方都停车的概率;
(3)只在一个地方停车的概率.
16.(本小题满分12分)
已知平面向量a=(![]() ,-1),b=(
,-1),b=(![]() ,
,![]() ),若存在不为零的实数k和角α,使向量c=a+ (sinα-3)b,d=-ka+(sinα)b,且c⊥d,试求实数k的取值范围.
),若存在不为零的实数k和角α,使向量c=a+ (sinα-3)b,d=-ka+(sinα)b,且c⊥d,试求实数k的取值范围.
17.(本小题满分13分)
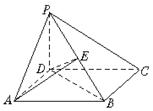 如图,四棱锥P—ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P—ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
求证:(1)平面PAC⊥平面PBD;
(2)求PC与平面PBD所成的角;
(3)在线段PB上是否存在一点E,使得PC⊥平面ADE?若存在,请加以证明,并求此时二面角A—ED—B的大小;若不存在,请说明理由.
18.(本小题满分13分)
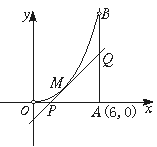 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
(1)试用t表示切线PQ的方程;
(2)试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[![]() ,64],试求出点P横坐标的取值范围.
,64],试求出点P横坐标的取值范围.
19.(本小题满分14分)
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足![]() ·
·![]() =0,
=0,![]() =-
=-![]()
![]() ,
,
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-1,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使得△ABE为等边三角形,求x0的值.
20.(本小题满分16分)
设f1(x)=![]() ,定义fn+1 (x)=f1[fn(x)],an=
,定义fn+1 (x)=f1[fn(x)],an=![]() ,其中n∈N*.
,其中n∈N*.
(1)求数列{an}的通项公式;
(2)若T2n=a1+2a2+3a3+…+2na2n,Qn=![]() ,其中n∈N*,试比较9T2n与Qn的大小,并说明理由.
,其中n∈N*,试比较9T2n与Qn的大小,并说明理由.
2004-2005届高考数学仿真试题(四)(广东)
参考答案
1.A 2.D 3.D 4.B 5.A 6.C 7.A 8.B 9.D 10.C
11.![]() 12.-13
13.1∶2∶3
14.①②
12.-13
13.1∶2∶3
14.①②![]() ③④或①③
③④或①③![]() ②④
②④
15.(1)P=![]() ×
×![]() ×
×![]() =
=![]() . 4分
. 4分
(2)P=![]() ×
×![]() ×
×![]() =
=![]() 8分
8分
(3)P=![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() =
=![]() . 12分
. 12分
16.∵c⊥d,
∴c·d=0, 2分
即[a+(sinα-3)b]·[-ka+(sinα)b]=0, 4分
也即-ka2+a·b·sinα-k(sinα-3)a·b+sinα(sinα-3)b2=0,
又∵a=(![]() ,-1),b=(
,-1),b=(![]() ,
,![]() ),
),
∴a·b=0,且a2=|a|2=4,b2=|b|2=1, 6分
∴-4k+sinα(sinα-3)=0, 8分
k=![]() (sinα-
(sinα-![]() )2-
)2-![]() , 10分
, 10分
而-1≤sinα≤1,
∴当sinα=-1时,k取最大值1;
当sinα=1时,k取最小值-![]() .
.
所以所求k的取值范围为[-![]() ,1] 12分
,1] 12分
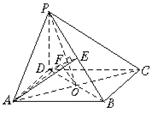 17.(1)∵PD⊥底面ABCD,
17.(1)∵PD⊥底面ABCD,
∴AC⊥PD,
又∵底面ABCD为正方形,
∴AC⊥BD,而PD与BD交于点D,
∴AC⊥平面PBD, 2分
又AC![]() 平面PAC,
平面PAC,
∴平面PAC⊥平面PBD. 4分
(2)记AC与BD相交于O,连结PO,由(1)知,
AC⊥平面PBD,
∴PC在平面PBD内的射影是PO,
∴∠CPO就是PC与平面PBD所成的角, 6分
∵PD=AD,
∴在Rt△PDC中,PC=![]() CD,
CD,
而在正方形ABCD中,OC=![]() AC=
AC=![]() CD,
CD,
∴在Rt△POC中,有∠CPO=30°.
即PC与平面PBD所成的角为30°. 8分
(3)在平面PBD内作DE⊥PO交PB于点E,连AE,
则PC⊥平面ADE.以下证明:
由(1)知,AC⊥平面PBD,
∴AC⊥DE,
又PO、AC交于点O,
∴DE⊥平面PAC,
∴DE⊥PC,(或用三垂线定理证明)
而PD⊥平面ABCD,∴PD⊥AD,
又∵AD⊥CD,∴AD⊥平面PCD,∴AD⊥PC,
∴PC⊥平面ADE,由AC⊥平面PBD,
∴过点O作OF⊥DE于F,
连AF,由三垂线定理可得,AF⊥DE,
∴∠OFA是二面角A—ED—B的平面角, 10分
设PD=AD=a,在Rt△PDC中,
求OF=![]() a,
a,
而AO=![]() a,
a,
∴在Rt△AOF中,∠OFA=60°,
即所求的二面角A—ED—B为60°. 13分
18.(1)设点M(t,t2),
又f′(x)=2x,
∴过点M的切线PQ的斜率为k=2t, 2分
∴切线PQ的方程为y-t2=2t(x-t),
即y=2tx-t2. 4分
(2)由(1)可求得P(![]() ,0),Q(6,12t-t2)
,0),Q(6,12t-t2)
∴g(t)=S△QAP=![]() (6-
(6-![]() t)(12t-t2)
t)(12t-t2)
=![]() t3-6t2+36t,(0<t<
t3-6t2+36t,(0<t<![]() , 6分
, 6分
由于g′(t)=![]() t2-12t+36,
t2-12t+36,
令g′(t)<0,则4<t<12,
又0<t<6,∴4<t<6,
∴g(t)的单调递减区间为(4,6),
因此m的最小值为4. 8分
(3)由(2)得,g(t)在(4,6)上递减,
∴此时S△QAP∈(g(6),g(4))=(54,64),
令g′(t)>0,得0<t<4,
∴g(t)在(0,4)上递增.
∴此时S△QAP∈(g(0),g(4))=(0,64),
又g(4)=64,
∴函数g(t)的值域为(0,![]() . 10分
. 10分
由![]() ≤g(t)≤64,得1≤t<6,
≤g(t)≤64,得1≤t<6,
∴![]() ≤
≤![]() <3,
<3,
∴点P的横坐标∈[![]() ,
,![]() . 13分
. 13分
19.(1)设点M的坐标为(x,y),由![]() =-
=-![]()
![]() ,得P(0,-
,得P(0,-![]() ),Q(
),Q(![]() ,0), 2分
,0), 2分
由![]() ·
·![]() =0,得(3,-
=0,得(3,-![]() )(x,
)(x,![]() )=0,
)=0,
又得y2=4x, 5分
由点Q在x轴的正半轴上,得x>0,
所以,动点M的轨迹C是以(0,0)为顶点,以(1,0)为焦点的抛物线,除去原点. 6分
(2)设直线l:y=k(x+1),
其中k≠0,代入y2=4x,
得k2x2+2(k2-2)x+k2=0,① 7分
设A(x1,y1),B(x2,y2),
则x1,x2是方程①的两个实根,
∴x1+x2=-![]() ,x1x2=1,
,x1x2=1,
所以,线段AB的中点坐标为(![]() ,
,![]() ), 9分
), 9分
线段AB的垂直平分线方程为
y-![]() =-
=-![]() (x-
(x-![]() ), 11分
), 11分
令y=0,x0=![]() +1,
+1,
所以点E的坐标为(![]() +1,0)
+1,0)
因为△ABE为正三角形,所以点E(![]() +1,0)到直线AB的距离等于
+1,0)到直线AB的距离等于![]() |AB|,
|AB|,
而|AB|=![]()
=![]() ·
·![]() , 13分
, 13分
所以,![]() =
=![]() ,
,
解得k=±![]() ,得x0=
,得x0=![]() . 14分
. 14分
20.(1)f1(0)=2,a1=![]() =
=![]() ,
,
fn+1(0)=f1[fn(0)]=![]() ,
,
an+1=![]() =
=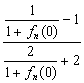 =
=![]()
=-![]()
![]() =-
=-![]() an, 4分
an, 4分
∴数列{an}是首项为![]() ,公比为-
,公比为-![]() 的等比数列,
的等比数列,
∴an=![]() (-
(-![]() )n-1. 6分
)n-1. 6分
(2)T2n=a1+2a2+3a3+…+(2n-1)a2n-1+2na2n,
-![]() T2n=(-
T2n=(-![]() a1)+(-
a1)+(-![]() )2a2+(-
)2a2+(-![]() )3a3+…+(-
)3a3+…+(-![]() )(2n-1)a2n-1+(-
)(2n-1)a2n-1+(-![]() )·2na2n
)·2na2n
=a2+2a3+…+(2n-1)a2n-na2n, 9分
两式相减得![]() T2n=a1+a2+a3+…+a2n+na2n,
T2n=a1+a2+a3+…+a2n+na2n,
所以,![]() T2n=
T2n=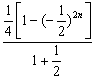 +n×
+n×![]() (-
(-![]() )2n-1=
)2n-1=![]() -
-![]() (-
(-![]() )2n+
)2n+![]() (-
(-![]() )2n-1, 11分
)2n-1, 11分
T2n=![]() -
-![]() (-
(-![]() )2n+
)2n+![]() (-
(-![]() )2n-1=
)2n-1=![]() (1-
(1-![]() ).
).
∴9T2n=1-![]() ,
,
Qn=1-![]() , 13分
, 13分
当n=1时,22n=4,(2n+1)2=9,∴9T2n<Qn;
当n=2时,22n=16,(2n+1)2=25,∴9T2n<Qn; 14分
当n≥3时,22n=[(1+1)n]2
=(C![]() +C
+C![]() +C
+C![]() +…+C
+…+C![]() )2>(2n+1)2,
)2>(2n+1)2,
∴9T2n>Qn. 16分