陕西远东一中02-03年高考数学模拟(四)
2003届国防科技工业
命 题:刘康宁
编 审:数学试题研究组
参考公式:
sin![]() cosβ=
cosβ=![]()
![]()
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
S台侧=![]() (c′+c)l
(c′+c)l
其中c′、c分别表示上下底面周长,l表示斜高或母线长
球的体积公式
V球=![]() πR3
πR3
其中R表示球的半径
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数![]() 在x=2时有最小值,则
在x=2时有最小值,则![]() 的一个值是
的一个值是
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.【理】极坐标平面内,定点P(1,![]() )到曲线
)到曲线![]() 上的点的最短距离是
上的点的最短距离是
A. 1
B.![]() C.
C.![]() D.
D.![]()
【文】已知点P(0,1),M是圆![]() 上任意一点,则PM的最小值是
上任意一点,则PM的最小值是
A.1
B.![]() C.
C.![]() D.
D.![]()
3.在下列四个正方体中,能得出PQ⊥MN的是
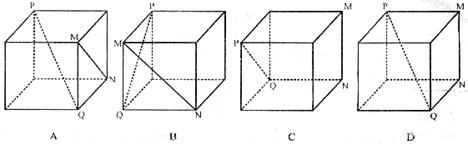
4.实数a、b、c满足![]() <
<![]() ,则下列不等式中成立的是
,则下列不等式中成立的是
A.a>b-c B.a<b+c
C.![]() >
>![]() D.
D.![]() <
<![]()
5.设全集为R,集合E=![]() <4或x>6
<4或x>6![]() ,F=
,F=![]() <x<4
<x<4![]() ,则
,则
A.![]() ∪F=R
B.E∪
∪F=R
B.E∪![]() =R
C.
=R
C.![]() ∪
∪![]() =R
D.E∪F=R
=R
D.E∪F=R
6.抛物线![]() (
(![]() >0)与直线ax+y-4=0的一个交点是(1,2),则抛物线
>0)与直线ax+y-4=0的一个交点是(1,2),则抛物线
的焦点到该直线的距离是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.Sn表示等差数列![]() 的前n项和,已知
的前n项和,已知![]() ,那么
,那么![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
8.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么,这个圆锥轴截面顶角的余弦值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
9.【理】设函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() 的值等于
的值等于
A.![]() B.
B. ![]() C. 0
D.
C. 0
D.![]()
【文】若![]()
A. -3 B. 3 C. -2 D.2
10.已知椭圆![]() 有公共的焦点,那么双曲线的渐近线方程是
有公共的焦点,那么双曲线的渐近线方程是
A. ![]() B.
B. ![]()
C.
![]() D.
D.![]()
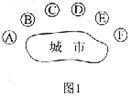 11.某市为改善生态环境,计划对城市外围A、B、C、D、E、
11.某市为改善生态环境,计划对城市外围A、B、C、D、E、
F六个区域(如图1)进行治理,第一期工程拟从这六个区域中
选取三个,根据要求至多有两个区域相邻,则不同的选取方案
共有
A.6 B.10
C.16 D.15
12.已知函数f(x)=ax2+bx+c(a≠0)在区间![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且对于任意实数x , f(x)≥0恒成立,则a+b+c的最小值是
上是减函数,且对于任意实数x , f(x)≥0恒成立,则a+b+c的最小值是
A.1 B.-1 C.2 D.-2
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.已知![]() 的展开式中不含x的项是
的展开式中不含x的项是![]() ,则正数a的值是_________。
,则正数a的值是_________。
 14.已知y=f(x)的反函数是f-1(x),且f-1(x)=
14.已知y=f(x)的反函数是f-1(x),且f-1(x)=
![]() ,
,![]() ,则方程f(x)=2003的解是_________。
,则方程f(x)=2003的解是_________。
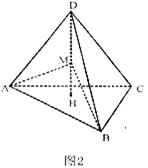
15.如图2,正四面体ABCD的棱长为1,H是顶点D的底面
ABC上的射影,M在DH上,且使得∠ABC=90°,则DM的长
为__________。
16.设双曲线![]() (a>0,b>0)的右准线与两条渐近线相交于A、B两点,F为右焦点,以AB为直径的圆恰过点F,则双曲线的离心率为_________。
(a>0,b>0)的右准线与两条渐近线相交于A、B两点,F为右焦点,以AB为直径的圆恰过点F,则双曲线的离心率为_________。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
在复平面上复数z1=2+i对应的点Z1,将向量![]() 沿顺时针方向旋转锐角
沿顺时针方向旋转锐角![]() 所得向量
所得向量![]() 对应的复数z2,且tg
对应的复数z2,且tg![]() =
=![]() 。若△ABC的内角A=argz1,B=argz2最长边为1。
。若△ABC的内角A=argz1,B=argz2最长边为1。
(Ⅰ)求角C的大小;
(Ⅱ)求△ABC的最短边的长。
18.(本小题满分12分)
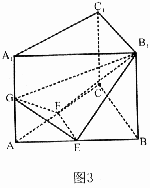 如图3,在直三棱柱ABC—A 1B 1C
1中,AC=BC=A 1A=2,∠ACB=90°,E、F、G分别是AB、AC、AA1的中点。
如图3,在直三棱柱ABC—A 1B 1C
1中,AC=BC=A 1A=2,∠ACB=90°,E、F、G分别是AB、AC、AA1的中点。
(Ⅰ)求证:B 1C1∥平面EFG;
(Ⅱ)求三棱锥B1-EFG的体积。
19.(本小题满分12分)
一艘轮船在航行过程中的燃料费与它的速度立方成正比例关系,其它与速度无关的费用为每小时96元。已知在速度为每小时10千米时,每小时的燃料费是6元。要使行驶1千米所需的费用总和最小,这艘轮船的速度应确定为每小时多少千米?
20.(本小题满分12分)
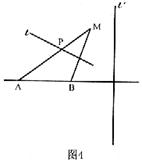 【理】如图4,A、B是两个定点,且AB=4。动点M到
【理】如图4,A、B是两个定点,且AB=4。动点M到
A点的距离是6,线段MB的垂直平分线![]() 交MA于点P
交MA于点P
,直线![]() ′垂直于直线AB,且B点到
′垂直于直线AB,且B点到![]() ′的距离为
′的距离为![]() 。若
。若
以AB所在直线为x轴,AB的垂平分线为y轴建直角坐标系。
(Ⅰ)求证:点P到点B的距离与到直线![]() ′的距离之比为定值;
′的距离之比为定值;
(Ⅱ)若点P到A、B两点的距离之积为m,当m取最大值时,
求P点的坐标。
【文】设各项均为正数的数列的前n项和为S n,且存在正数t,使得对所有正整数n,都有![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)如果![]()
![]() <t,求t的取值范围。
<t,求t的取值范围。
21.(本小题满分12分)
【理】已知数列![]() 的前三项依次为
的前三项依次为![]() ,
,![]() ,
,![]() ,前n项和为S n,且Sn=an3+bn2+cn(a、b、c∈R)。
,前n项和为S n,且Sn=an3+bn2+cn(a、b、c∈R)。
(Ⅰ)求S n的表达式;
(Ⅱ)若数列![]() 满足b n=an+1-an,
满足b n=an+1-an,![]() 为数列
为数列![]() 的前n项和,试求使得
的前n项和,试求使得![]() -2003取得最小值的n的值;
-2003取得最小值的n的值;
 (Ⅲ)若Tn=
(Ⅲ)若Tn=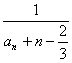 ,求证:
,求证:![]() <
<![]() (n≥2)。
(n≥2)。
【文】如图5,A、B是两个定点,且AB=4。动点M到
A点的距离是6,线段MB的垂直平分线![]() 交MA于点P。
交MA于点P。
直线![]() ′垂直于直线AB,且B点到
′垂直于直线AB,且B点到![]() ′的距离为
′的距离为![]() 。若以
。若以
AB所在直线为x轴,AB的垂直平分线为y轴建立直角坐标系。
(Ⅰ)求证:点P点到点B的距离与到直线![]() ′的距离之比为定值;
′的距离之比为定值;
(Ⅱ)若点P到A、B两点的距离之积为m,当m取最大值时,求P点的坐标。
22.(本小题满分14分)
【理】已知函数f(x)对任意的x∈R都有f(x)=1-![]() ,且f(0)=m(m>0,且m≠1)。
,且f(0)=m(m>0,且m≠1)。
(Ⅰ)求f(2)及f(4)的值;
(Ⅱ)求证:f(x)是周期函数,并求出它的一个周期;
(Ⅲ)若f(1)=![]() ,求f(22n+7)的值(n∈N)。
,求f(22n+7)的值(n∈N)。
【文】已知函数f(x)=![]() (a>0,a≠1),对定义域内的任意x都有f(2-x)+f(2+x)=0。
(a>0,a≠1),对定义域内的任意x都有f(2-x)+f(2+x)=0。
(Ⅰ)求实数m的值;
(Ⅱ)若当![]() 时,f(x)的取值范围恰为
时,f(x)的取值范围恰为![]() ,求实数a、b的值。
,求实数a、b的值。