北京朝阳02-03年高考数学(文)模拟(二)

数  学（文史类）

　　　本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。

第Ⅰ卷（选择题， 共50分）

参考公式：

　　　 三角函数的和差化积公式　　　　　　　　　　  正棱台、圆台的侧面积公式

　　　 　　　　 

　　　　  其中、分别表示上、下底面

　 　　　　　 周长，表示斜高或母线长

　　　　　　　　　　　　　　　　　　　　　 球体的体积公式

　　　　　　 其中R表示的半径

一、选择题：本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，

只有一项是符合题目要求的。

1．已知全集I={1，2，3，4，5}，A∩B={2}，，则等于　　　　　　　（　　）

　　　 A．{3}　　　　　　　　　　 B．{5}　　　　　　　　　　 C．{1，2，4}　　　　　D．{3，5}

2．若，下列关系式中不成立的个数是　　　　　　　　　　　　　　　　　　　（　　）

　　　 ①　　　　　　　　　　　　　　　　　　　　　　　②

　　　 ③　　　　　　　　　　　　　　　　　④

　　　 A．4个　　　　　　　　　　B．3个　　　　　　　　　　C．2个　　　　　　　　　　D．1个

3．一个半径为的半球内切于轴截面顶角为的圆锥，半球的底面在圆锥的底面内，则

　　等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　B．2：1　　　　　　　　　

　　　 C．2：　　　　　　　　　　　　　　　　　　　　　　　D．1：2

4．若双曲线的离心率为2，则双曲线的离心率为

　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　　　D．2

5．把y=cosx的图象上所有点的横坐标缩小到原来的一半，纵坐标不变，然后把图象向左平移单位，得到新的函数图象，其解析式为　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　D．

6．在北纬45°圈上有M、N两地，它们 在纬度圈上的弧长是（R是地球的半径），

　 则M、N两地的球面距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　　 D．

7．在△ABC中，若且A、B为锐角，那么C为锐角的充要条件是（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　 B．　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　D．

8．6个乒乓球运动员，每两个人都可以组成一对双打选手，从中选出两对双打选手的选法有

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．15种　　　　　　　　　　　　　　　　　　　　　　　　　B．90种　　　　　　　　　

　　　 C．105种　　　　　　　　　　　　　　　　　　　　　　　　D．110种

9．在数列中，则等于　　　　　　　　　　　　　 （　　）

　　　 A．81　　　　　　　　　　　　　　　　　　　　　　　　　　　B．50　　　　　　　　　　　

　　　 C．－13　　　　　　　　　　　　　　　　　　　　　　　　　D．－46

10．两游泳者在50米游泳池的对边上同时开始游泳，1人以每秒2.5米、另一人以每秒

　 米的速度进行，他们游了4分种，若不计转向时的时间，则他们迎面闪过的次数为（　　）

　　　 A．7次　　　　　　　　　　　　　　　　　　　　　　　　　 B．8次　　　　　　　　　　

　　　 C．9次　　　　　　　　　　　　　　　　　　　　　　　　　 D．10次

第Ⅱ卷（非选择题， 共100分）

二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中横线上.

11．函数的单调递减区间是　　　　  .

12．抛物线的通径（过焦点垂直于轴的弦）的长为　　　　　  .

13．圆锥的轴截面为等边三角形SAB，S为顶点，C是底面圆周上AB的三等分点，

AC=CB，则二面角C—SA—B的正切值为　　　　　 .

14．已知曲线：C₁：y²=ax,与C₁关于点（1，1）对称的曲线为C₂，且C₁、C₂有两个不同的交点，如果过这两个交点的直线的倾斜角为45°，那么实数a的值是　　　　　  .

三、解答题：本大题共6小题，共84分. 解答应写出文字说明，证明过程或演算步骤.

15．（本小题满分14分）

设非零复数满足为纯虚数， 求、.

16．（本小题满分14分）

　　　 关于的方程的解都大于1. 求实数的取值范围.

17．（本小题满分14分）

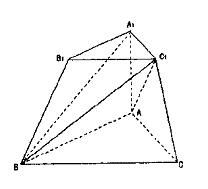
　　　 在三棱台ABC—A₁B₁C₁中，侧棱A₁A⊥底面ABC，且AC=BC₁=2A₁C₁，

∠BAC=∠BC₁C=90°.

　　　 （Ⅰ）求证：CC₁⊥平面ABC₁；

　　　 （Ⅱ）求AC与BC₁所成的角；

　　　 （Ⅲ）若A₁C₁=，求AA₁的长.

18．（本小题满分14分）

　　　 2002年底某县的绿化面积只占全县总面积的40%，从2003年开始，计划每年将非绿化面积的8%绿化，由于修路和盖房等用地，原有绿化面积的2%被非绿化.

　　　 （Ⅰ）设该县的总面积为1，2002年底绿化面积为，经过年后绿化的面积为求证：

　　　 （Ⅱ）求数列的第项；

　　　 （Ⅲ）至少需要多少年的努力，才能使绿化率超过60%.（

19．（本小题满分14分）

　　　 已知：函数在（－1，1）上有定义，且满足、有

　　　 （Ⅰ）求

　　　 （Ⅱ）证明在上为奇函数；

　　　 （Ⅲ）在数列中， 求f(x_n)

20．（本小题满分14分）

　　　 已知：椭圆

　　　 （Ⅰ）若点P是椭圆C内部一点，求证：

　　　 （Ⅱ）若椭圆上存在不同的两点关于直线对称，试求、满足的关系式.