试卷类型：A
2003年MAM高考数学仿真试题(四)
MAM: M-March A-April M-May
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟
第Ⅰ卷(选择题 共60分)
注意事项：
1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上
2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.
3.考试结束，监考人将本试卷和答题卡一并收回.
一、选择题（本大题共12小题，每小题5分，共60分.在每小题的四个选项中，只有一项是符合题目要求的）
1.已知函数y=f(x)的反函数f-–1(x)=2x+1，则f(1)等于
A.0 B.1 C.－1 D.4
2.小王打算用70元购买面值分别为20元和30元的两种IC卡电话卡.若他至少买一张，则不同的买法一共有_____________种
A.5 B.6 C.7 D.8
3.已知直线l1：x+ay+3=0与直线l2：x-2y+1=0垂直，则a的值为
A.2 B.－2 C.
－
D.
4.对于函数f(x)=ax2+bx+c(a≠0)作代换x=g(t)，则不改变函数f(x)的值域的代换是
A.g(t)=2t B.g(t)=t C.g(t)=sint D.g(t)=log2t
5.函数y=4sin(
+x)sin(-x)是
A.周期为2π的偶函数 B.周期为2π的奇函数
C.周期为π的偶函数 D.周期为π的奇函数
6.把长12厘米的细铁丝截成两段，各自围成一个正三角形，那么这两个正三角形面积之和的最小值是
A.
cm2 B.4
cm2
C.3
cm2 D.2
cm2
7.在北纬45°圈上有甲、乙两地，它们的经度分别是东经140°与西经130°，设地球半径为R，则甲、乙两地的球面距离是
A.πR B.
πR
C.
πR D.
πR
8.在等差数列{an}中，a1+a15=24,则a2+a16－a10的值为
A.24 B.12 C.20 D.－8
9.已知抛物线C1：y=2x2与抛物线C2关于直线y=－x对称，则C2的准线方程是
A.x=－
B.x=
C.x= D.x=－
10.学校要从4名爱好摄影的同学中选派3名分别参加校外摄影小组的3期培养（每期只派1名），由于时间上的冲突，甲、乙两人都不能参加第1期培训，则不同的选派方式有
A.6种 B.8种 C.12种 D.16种
11.将函数y=x+2的图象按a=（6，－2）平移后，得到的新图象的解析式为
A.y=x+10 B.y=x－6
C.y=x+6 D.y=x－10
12.△ABC中，AB=9，AC=15，∠BAC=120°，△ABC所在平面外一点P到三个顶点A、B、C的距离都是14，那么点P到平面α的距离为
A.7 B.9 C.11 D.13
MAM高考数学仿真试题(四)
第Ⅱ卷(非选择题 共90分)
注意事项：
1.第Ⅱ卷，用钢笔或圆珠笔直接答在试题卷中.
2.答卷前将密封线内的项目填写清楚.
| 题 号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分 数 | ||||||||
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13.在（1+x）5+(1+x)6+(1+x)7的展开式中，x4项的系数是____________.
14.双曲线与椭圆9x2+25y2=225有相同的焦点，且过点(3,-1)，则双曲线的渐近线方程是_____________.
15.如果tan(α+β)=
,tan(β－)=,那么tan(α+)的值是_____________.
16.正三棱锥的一个侧面的面积与底面积之比为2︰3，则这个三棱锥的侧面和底面所成二面角的度数为_____________
三、解答题（本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17.（本小题满分12分）
已知函数f(x)=sin(x+
)+sin(x－)+cosx+a(a∈R,a是常数).
（1）求函数f(x)的最小正周期；
（2）若x∈［－
,］时，f(x)的最大值为1，求a的值.
18.（本小题满分12分）
设人的某一特征（如眼睛大小）是由他一对基因所决定，以d表示显性基因，r表示隐性基因，则具有dd基因的人为纯显性，具有rr基因的人为纯隐性，具有rd基因的人为混合性.纯显性与混合性都显露显性基因决定的某一特征，孩子从父母身上各得到一个基因，假定父母都是混合性，问：
（1）1个孩子有显性决定特征的概率是多少？
（2）2个孩子中至少有一个显性决定的特征的概率是多少？
19.（本小题满分12分）
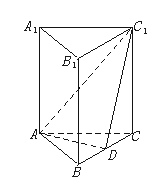
如图，正三棱柱各棱都相等，D是BC上一点，AD⊥C1D
（1）求证：截面ADC1⊥侧面BCC1B1；
（2）求二面角C—AC1—D的大小.
20.（本小题满分12分）
已知二次函数f(x)=ax2+bx(a,b为常数且a≠0)满足条件：
f(－x+5)=f(x－3),且方程f(x)=x有等根.
（1）求f(x)的解析式；
（2）是否存在实数m,n(m＜n),使f(x)的定义域和值域分别是［m,n］和［3m,3n］?如果存在，求出m,n的值；若不存在，说明理由.
21.（本小题满分12分）
椭圆
=1(a＞b＞0)的两焦点为F1(0,－c),F2(0,c)(c＞0),离心率e=
,焦点到椭圆上点的最短距离为2-.
(1)求椭圆的方程；
（2）设P、Q为椭圆与直线y=x+1两个交点，求tanPOQ的值.
22.（本小题满分14分）
有一条生产流水线，由于改进了设备，预计第一年产量的增长率为150%，以后每年的增长率是前一年的一半，设原来的产量为a.
(1)写出改进设备后的第一年，第二年，第三年的产量，并写出第n年与第n-1年（n≥2,n∈N+）的产量之间的关系式；
（2）由于设备不断老化，估计每年将损失年产量的10%，照这样下去，以后每年的产量是否始终是逐年提高？若是，请给予证明；若不是，请说明从第几年起，产量将比上一年减少.