06 直线与圆
一、选择题
1.(安徽10)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 有公共点,则直线
有公共点,则直线![]() 的斜率的取值范围为( D )
的斜率的取值范围为( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.(安徽11)若![]() 为不等式组
为不等式组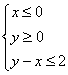 表示的平面区域,则当
表示的平面区域,则当![]() 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线![]() 扫过
扫过![]() 中的那部分区域的面积为 ( C )
中的那部分区域的面积为 ( C )
A.![]() B.1 C.
B.1 C.![]() D.5
D.5
3.(北京6)若实数![]() 满足
满足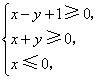 则
则![]() 的最小值是( A )
的最小值是( A )
A.0 B.![]() C.1 D.2
C.1 D.2
4.(福建10)若实数x、y满足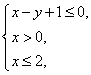 则
则![]() 的取值范围是( D )
的取值范围是( D )
A.(0,2) B.(0,2) C.(2,+∞) D.[2,+∞)
5.(广东6)经过圆x2+2x+y2=0的圆心G,且与直线x+y=0垂直的直线方程是( C )
A.x-y+1=0 B.x-y-1=0
C.x+y-1=0 D.x+y+1=0
6.(宁夏10)点![]() 在直线
在直线![]() 上,且
上,且![]() 满足
满足![]() ,则点
,则点![]() 到坐标原点距离的取值范围是( B )
到坐标原点距离的取值范围是( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(湖南3)已条变量![]() 满足
满足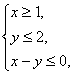 则
则![]() 的最小值是( C )
的最小值是( C )
A.4 B.3 C.2 D.1
8.(辽宁3)圆![]() 与直线
与直线![]() 没有公共点的充要条件是( B
)
没有公共点的充要条件是( B
)
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
9.(辽宁9)已知变量![]() 满足约束条件
满足约束条件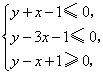 则
则![]() 的最大值为( B )
的最大值为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.(全国Ⅰ10)若直线![]() 与圆
与圆![]() 有公共点,则( D )
有公共点,则( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.(全国Ⅱ3)原点到直线![]() 的距离为( D )
的距离为( D )
A.1 B.![]() C.2 D.
C.2 D.![]()
12.(全国Ⅱ6) 设变量![]() 满足约束条件:
满足约束条件: ,则
,则![]() 的最小值为( D )
的最小值为( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.(山东11) 若圆![]() 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线![]() 和
和![]() 轴相切,则该圆的标准方程是( B )
轴相切,则该圆的标准方程是( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.(上海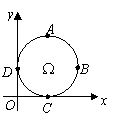 15)如图,在平面直角坐标系中,
15)如图,在平面直角坐标系中,![]() 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域(含边界),A、B、C、D是该圆的四等分点.若点![]() 、点
、点![]() 满足
满足![]() 且
且![]() ,则称P优于
,则称P优于![]() .如果
.如果![]() 中的点
中的点![]() 满足:不存在
满足:不存在![]() 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( D )
中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( D )
A.![]()
![]() B.
B.![]()
C.![]() D.
D.![]()
15.(四川6)直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() ,再向右平移1个单位,所得到的直线为( A )
,再向右平移1个单位,所得到的直线为( A )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
16.(天津2) 设变量![]() 满足约束条件
满足约束条件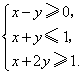 则目标函数
则目标函数![]() 的最大值为( D
)
的最大值为( D
)
A.2 B.3 C.4 D.5
17.(浙江10)若![]() ,且当
,且当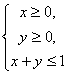 时,恒有
时,恒有![]() ,则以
,则以![]() ,b为坐标点
,b为坐标点![]() 所形成的平面区域的面积等于 (
C )
所形成的平面区域的面积等于 (
C )
(A)![]() (B)
(B)![]() (C)1
(D)
(C)1
(D)![]()
18.(重庆3)曲线C:![]() (
(![]() 为参数)的普通方程为 (
C )
为参数)的普通方程为 (
C )
(A)(x-1)2+(y+1)2=1 (B) (x+1)2+(y+1)2=1
(C) (x-1)2+(y-1)2=1 (D) (x-1)2+(y-1)2=1
19.(重庆4)若点P分有向线段![]() 所成的比为-
所成的比为-![]() ,则点B分有向线段
,则点B分有向线段![]() 所成的比是( A )
所成的比是( A )
(A)-![]() (B)-
(B)-![]() (C)
(C)
![]() (D)3
(D)3
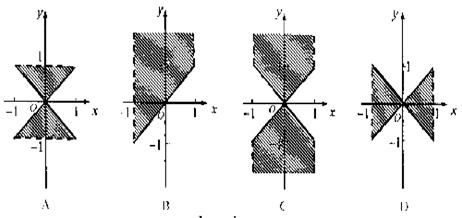
20.(湖北5).在平面直角坐标系![]() 中,满足不等式组
中,满足不等式组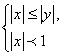 的点
的点![]() 的集合用阴影表示为下列图中的 ( C )
的集合用阴影表示为下列图中的 ( C )
21.(陕西5) 直线![]() 与圆
与圆![]() 相切,则实数
相切,则实数![]() 等于( A )
等于( A )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
二、填空题
1.(福建14)若直线3x+4y+m=0与圆x2+y2-2x+4y+4=0没有公共点,则实数m的取值范围是 ______________. ![]()
2.(广东12)若变量x,y满足 则z=3x+2y的最大值是________.70
则z=3x+2y的最大值是________.70
3.(湖南14)将圆![]() 沿x轴正向平移1个单位后所得到圆C,则圆C的方程是________,若过点(3,0)的直线
沿x轴正向平移1个单位后所得到圆C,则圆C的方程是________,若过点(3,0)的直线![]() 和圆C相切,则直线
和圆C相切,则直线![]() 的斜率为_____________.
的斜率为_____________.
![]() ;
; ![]()
4.(江苏9)在平面直角坐标系中,设三角形![]() 的顶点分别为
的顶点分别为![]() ,点P(0,p)在线段AO上(异于端点),设
,点P(0,p)在线段AO上(异于端点),设![]() 均为非零实数,直线
均为非零实数,直线![]() 分别交
分别交![]() 于点
于点![]() ,一同学已正确算的
,一同学已正确算的![]() 的方程:
的方程:![]() ,请你求
,请你求![]() 的方程: ( )
的方程: ( )![]() (
(![]() )
)
5.(全国Ⅰ13)若![]() 满足约束条件
满足约束条件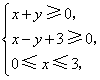 则
则![]() 的
的
最大值为 .9
6.(山东16) 设![]() 满足约束条件
满足约束条件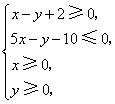
则![]() 的最大值为
.11
的最大值为
.11
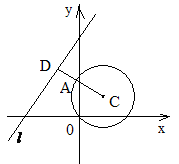 7.(上海11)在平面直角坐标系中,点
7.(上海11)在平面直角坐标系中,点![]() 的坐标分别为
的坐标分别为![]() .如果
.如果![]() 是
是![]() 围成的区域(含边界)上的点,那么当
围成的区域(含边界)上的点,那么当![]() 取到最大值时,点
取到最大值时,点![]() 的坐标是 ______ .
的坐标是 ______ .![]()
8.(四川14)已知直线![]() 与圆
与圆![]() ,
,
则![]() 上各点到
上各点到![]() 的距离的最小值为_______
的距离的最小值为_______![]() ______。
______。
9.(天津15) 已知圆![]() 的圆心与点
的圆心与点![]() 关于直线
关于直线![]() 对称.
对称.
直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,
两点,
![]() 且
且![]() ,则圆
,则圆![]() 的方程为
.
的方程为
.
10.(重庆15)已知圆C: ![]() (a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a=
.-2
(a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a=
.-2
11.
12.(湖北15).圆![]() 的圆心坐标为 (3,-2),和圆C关于直线
的圆心坐标为 (3,-2),和圆C关于直线![]() 对称的圆C′的普通方程是
. (x+2)2+(y-3)2=16
对称的圆C′的普通方程是
. (x+2)2+(y-3)2=16
三、解答题
1.(宁夏20)(本小题满分12分)
已知![]() ,直线
,直线![]() :
:![]() 和圆
和圆![]() :
:![]() .
.
(Ⅰ)求直线![]() 斜率的取值范围;
斜率的取值范围;
(Ⅱ)直线![]() 能否将圆
能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
解:(Ⅰ)直线![]() 的方程可化为
的方程可化为![]() ,
,
直线![]() 的斜率
的斜率![]() ,····························································································· 2分
,····························································································· 2分
因为![]() ,
,
所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
所以,斜率![]() 的取值范围是
的取值范围是![]() .········································································· 5分
.········································································· 5分
(Ⅱ)不能.················································································································ 6分
由(Ⅰ)知![]() 的方程为
的方程为
![]() ,其中
,其中![]() .
.
圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
圆心![]() 到直线
到直线![]() 的距离
的距离
![]() .·············································································································· 9分
.·············································································································· 9分
由![]() ,得
,得![]() ,即
,即![]() .从而,若
.从而,若![]() 与圆
与圆![]() 相交,则圆
相交,则圆![]() 截直线
截直线![]() 所得的弦所对的圆心角小于
所得的弦所对的圆心角小于![]() .
.
所以![]() 不能将圆
不能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段弧. 12分
的两段弧. 12分
2.(江苏18)(16分)
设平面直角坐标系xoy中,设二次函数![]() 的图像与两坐标轴有三个交点,经过这三个交点的圆记为C。求:
的图像与两坐标轴有三个交点,经过这三个交点的圆记为C。求:
(1)求实数b的取值范围
(2)求圆C的方程
(3)问圆C是否经过某定点(其坐标与b无关)?请证明你的结论。
【解析】:本小题考查二次函数图像和性质、圆的方程的求法。
(1)令x=0,得抛物线于y轴的交点是(0,b)
令f(x)=0,得x2+2x+b=0,由题意b≠0且△>0,解得b<1且b≠0
(2)设所求圆的一般方程为x2+ y2+Dx+Ey+F=0
令y=0,得x2+Dx+F=0,这与x2+2x+b=0是同一个方程,故D=2,F=b
令x=0,得y2+ Ey+b=0,此方程有一个根为b,代入得E=-b-1
所以圆C的方程为x2+ y2+2x -(b+1)y+b=0
(3)圆C必过定点(0,1),(-2,1)
证明如下:将(0,1)代入圆C的方程,得左边= 02+ 12+2×0-(b+1)×1+b=0,右边=0
所以圆C必过定点(0,1);
同理可证圆C必过定点(-2,1)。