08 立体几何
一、选择题
1.(安徽3).已知![]() 是两条不同直线,
是两条不同直线,![]() 是三个不同平面,下列命题中正确的是省( B )
是三个不同平面,下列命题中正确的是省( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
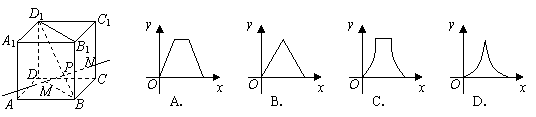
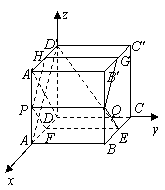
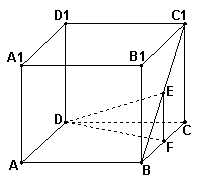
2.(北京8)如图,动点![]() 在正方体
在正方体![]() 的对角线
的对角线![]() 上,过点
上,过点![]() 作垂直于平面
作垂直于平面![]() 的直线,与正方体表面相交于
的直线,与正方体表面相交于![]() .设
.设![]() ,
,![]() ,则函数
,则函数![]() 的图象大致是( B )
的图象大致是( B )
3.(福建6)如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
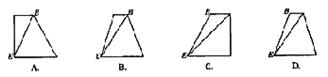
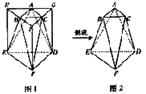
4.(广东7)将正三棱柱截去三个角(如图1所示A,B,C分别是△CHI三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( A )
5.(宁夏12)已知平面![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() ,则下列四种位置关系中,不一定成立的是( D )
,则下列四种位置关系中,不一定成立的是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(湖南5)已知直线m,n和平面![]() 满足
满足![]() ,则 ( D )
,则 ( D )
![]()
![]() 或
或![]()
![]()
![]() 或
或![]()
7.(湖南9)长方体![]() 的8个顶点在同一个球面上,且AB=2,AD=
的8个顶点在同一个球面上,且AB=2,AD=![]() ,
,
![]() ,则顶点A、B间的球面距离是( B )
,则顶点A、B间的球面距离是( B )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2![]()
8.(江西9).设直线![]() 与平面
与平面![]() 相交但不垂直,则下列说法中正确的是( B )
相交但不垂直,则下列说法中正确的是( B )
A.在平面![]() 内有且只有一条直线与直线
内有且只有一条直线与直线![]() 垂直
垂直
B.过直线![]() 有且只有一个平面与平面
有且只有一个平面与平面![]() 垂直
垂直
C.与直线![]() 垂直的直线不可能与平面
垂直的直线不可能与平面![]() 平行
平行
D.与直线![]() 平行的平面不可能与平面
平行的平面不可能与平面![]() 垂直
垂直
9.(辽宁12)在正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,则在空间中与三条直线
的中点,则在空间中与三条直线![]() ,
,![]() ,
,![]() 都相交的直线( D )
都相交的直线( D )
A.不存在 B.有且只有两条 C.有且只有三条 D.有无数条
10.(全国Ⅰ11)已知三棱柱![]() 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,![]() 在底面
在底面![]() 内的射影为
内的射影为![]() 的中心,则
的中心,则![]() 与底面
与底面![]() 所成角的正弦值等于( B )
所成角的正弦值等于( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.(全国Ⅱ8)正四棱锥的侧棱长为![]() ,侧棱与底面所成的角为
,侧棱与底面所成的角为![]() ,则该棱锥的体积为( B )
,则该棱锥的体积为( B )
A.3 B.6 C.9 D.18
12.(全国Ⅱ12)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( C )
A.1 B.![]() C.
C.![]() D.2
D.2
13.(山东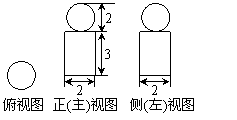 6) 右图是一个几何体的三视图,根据图中数据,
6) 右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.(上海13)给定空间中的直线l及平面![]() .条件“直线l与平面
.条件“直线l与平面![]() 内两条相交直线都垂直”是“直线l与平面
内两条相交直线都垂直”是“直线l与平面![]() 垂直”的( C )
垂直”的( C )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
15.(四川8)设![]() 是球心
是球心![]() 的半径
的半径![]() 的中点,分别过
的中点,分别过![]() 作垂直于
作垂直于![]() 的平面,截球面得两个圆,则这两个圆的面积比值为:( D )
的平面,截球面得两个圆,则这两个圆的面积比值为:( D )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
16.(四川 10)设直线
10)设直线![]() 平面
平面![]() ,过平面
,过平面![]() 外一点
外一点![]() 与
与![]() 都成
都成![]() 角的直线有且只有:( B )
角的直线有且只有:( B )
(A)1条 (B)2条 (C)3条 (D)4条
17.(四川12)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为![]() 的菱形,则该棱柱的体积等于( B )
的菱形,则该棱柱的体积等于( B )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
18.(天津5) 设![]() 是两条直线,
是两条直线,![]() 是两个平面,则
是两个平面,则![]() 的一个充分条件是( C
)
的一个充分条件是( C
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
19.(浙江9)对两条不相交的空间直线![]() 和
和![]() ,必定存在平面
,必定存在平面![]() ,使得 ( B
)
,使得 ( B
)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
20.(重庆11)如题(11)图,模块①-⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为 ( A )
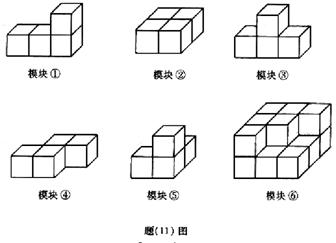
(A)模块①,②,⑤ (B)模块①,③,⑤
(C)模块②,④,⑥ (D)模块③,④,⑤
21.(湖北4).用与球必距离为1的平面去截面面积为![]() ,则球的体积为 ( D )
,则球的体积为 ( D )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
22.(陕西8)长方体![]() 的各顶点都在半径为1的球面上,其中
的各顶点都在半径为1的球面上,其中![]() ,则两
,则两![]() 点的球面距离为( C )
点的球面距离为( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
23.(陕西10) 如图,![]() 到
到![]() 的距离分别是
的距离分别是![]() 和
和![]() ,
,![]() 与
与![]() 所成的角分别是
所成的角分别是![]() 和
和![]() ,
,![]() 在
在![]() 内的射影分别是
内的射影分别是![]() 和
和![]() ,若
,若![]() ,则( D )
,则( D )
 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题
1.(安徽16)已知点![]() 在同一个球面上,
在同一个球面上,![]()
![]() 若
若![]()
![]()
![]() ,则
,则![]() 两点间的球面距离是
两点间的球面距离是
![]()
2.(福建15)若三棱锥的三条侧棱两两垂直,且侧棱长均为
![]() ,则其外接球的表面积是 . 9
,则其外接球的表面积是 . 9![]() 3.(广东15)(几何证明选讲选做题)已知PA是圆O的切点,切点为A,PA=2.AC是圆O的直径,PC与圆O交于B点,PB=1,则圆O的半径R=________.
3.(广东15)(几何证明选讲选做题)已知PA是圆O的切点,切点为A,PA=2.AC是圆O的直径,PC与圆O交于B点,PB=1,则圆O的半径R=________.![]()
4.(宁夏14)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为![]() ,底面周长为3,则这个球的体积为 .
,底面周长为3,则这个球的体积为 .![]()
5.(江西15)连结球面上两点的线段称为球的弦.半径为4的球的两条弦![]() 的长度分别等于
的长度分别等于![]() 、
、![]() ,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为
.5
,每条弦的两端都在球面上运动,则两弦中点之间距离的最大值为
.5
6.(辽宁14)在体积为![]() 的球的表面上有A、B,C三点,AB=1,BC=
的球的表面上有A、B,C三点,AB=1,BC=![]() ,A,C两点的球面距离为
,A,C两点的球面距离为![]() ,则球心到平面ABC的距离为_________.
,则球心到平面ABC的距离为_________.![]()
7.(全国Ⅰ16)已知菱形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 将
将![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,则点
,则点![]() 到
到![]() 所在平面的距离等于
.
所在平面的距离等于
.![]()
8.(全国Ⅱ16)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ;
充要条件② .
(写出你认为正确的两个充要条件)
两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.
注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.
9.(浙江15)已知球O的面上四点A、B、C、D,DA![]() 平面ABC,AB
平面ABC,AB![]() BC,DA=AB=BC=
BC,DA=AB=BC=![]() ,则球O点体积等于 。
,则球O点体积等于 。![]()
10.(天津13) 若一个球的体积为![]() ,则它的表面积为
.
,则它的表面积为
.![]()
三、解答题
1.(安徽19).(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 四边长为1的 菱形,
四边长为1的 菱形,![]() ,
, ![]() ,
, ![]() ,
,![]() 为
为![]() 的中点。
的中点。
(Ⅰ)求异面直线AB与MD所成角的大小![]() ;
;
(Ⅱ)求点B到平面OCD的距离。
方法一(综合法)
(1)![]()

![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角(或其补角)
所成的角(或其补角)
作![]() 连接
连接![]()
![]()
![]()
![]() ,
,![]()
所以 ![]() 与
与![]() 所成角的大小为
所成角的大小为![]()
(2)![]() 点A和点B到平面OCD的距离相等,
点A和点B到平面OCD的距离相等,
连接OP,过点A作![]() 于点Q,
于点Q,
![]()
![]()
又 ![]() ,线段AQ的长就是点A到平面OCD的距离
,线段AQ的长就是点A到平面OCD的距离
![]() ,
,![]()
 ,所以点B到平面OCD的距离为
,所以点B到平面OCD的距离为![]()
方法二(向量法)
作![]() 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为![]() 轴建立坐标系
轴建立坐标系
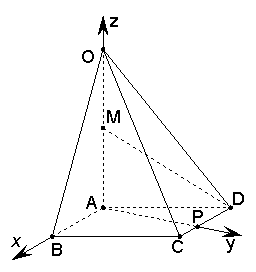
![]() ,
,
(1)设![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
![]()
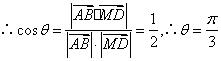 ,
,
![]()
![]() 与
与![]() 所成角的大小为
所成角的大小为![]()
(2) ![]()
![]() 设平面OCD的法向量为
设平面OCD的法向量为![]() ,则
,则![]()
即 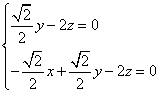
取![]() ,解得
,解得![]()
设点B到平面OCD的距离为![]() ,则
,则![]() 为
为![]() 在向量
在向量![]() 上的投影的绝对值,
上的投影的绝对值,
![]() ,
, 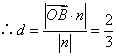 .
.
所以点B到平面OCD的距离为![]()
2.(北京16)(本小题共14分)
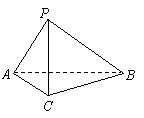 如图,在三棱锥
如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解法一:
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
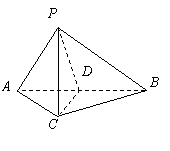
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)![]() ,
,![]() ,
,
![]() .
.
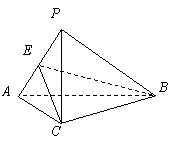 又
又![]() ,
,
![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
解法二:
(Ⅰ)![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
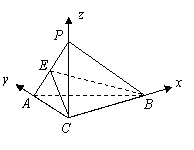
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
则![]() .
.
设![]() .
.
![]() ,
,
![]() ,
,![]() .
.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,![]() ,
,
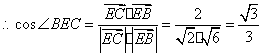 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
3.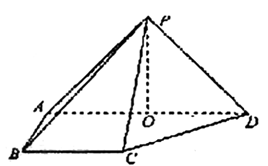 (福建19)(本小题满分12分)
(福建19)(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
解法一:
(Ⅰ)证明:在△PAD卡中PA=PD,O为AD中点,所以PO⊥AD.
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO![]() 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
(Ⅱ)连结BO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,
所以OB∥DC.
由(Ⅰ)知PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=![]() ,
,
在Rt△POA中,因为AP=![]() ,AO=1,所以OP=1,
,AO=1,所以OP=1,
在Rt△PBO中,PB=![]() ,
,
cos∠PBO=![]() ,
,
所以异面直线PB与CD所成的角的余弦值为![]() .
.
(Ⅲ)由(Ⅱ)得CD=OB=![]() ,
,
在Rt△POC中,PC=![]() ,
,
 所以PC=CD=DP,S△PCD=
所以PC=CD=DP,S△PCD=![]() ·2=
·2=![]() .
.
又S△=![]()
设点A到平面PCD的距离h,
由VP-ACD=VA-PCD,
得![]() S△ACD·OP=
S△ACD·OP=![]() S△PCD·h,
S△PCD·h,
即![]() ×1×1=
×1×1=![]() ×
×![]() ×h,
×h,
解得h=![]() .
.
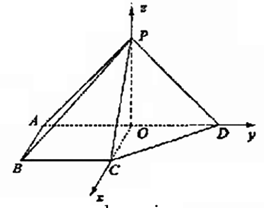 解法二:
解法二:
(Ⅰ)同解法一,
(Ⅱ)以O为坐标原点,![]() 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz.
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz.
则A(0,-1,0),B(1,-1,0),C(1,0,0),
D(0,1,0),P(0,0,1).
所以![]() =(-1,1,0),
=(-1,1,0),![]() =(t,-1,-1),
=(t,-1,-1),
∞〈![]() 、
、![]() 〉=
〉=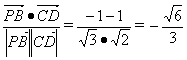 ,
,
所以异面直线PB与CD所成的角的余弦值为![]() ,
,
(Ⅲ)设平面PCD的法向量为n=(x0,y0,x0),
由(Ⅱ)知![]() =(-1,0,1),
=(-1,0,1),![]() =(-1,1,0),
=(-1,1,0),
![]()
![]() 则 n·
则 n·![]() =0,所以 -x0+ x0=0,
=0,所以 -x0+ x0=0,
n·![]() =0, -x0+ y0=0,
=0, -x0+ y0=0,
即x0=y0=x0,
取x0=1,得平面的一个法向量为n=(1,1,1).
又![]() =(1,1,0).
=(1,1,0).
从而点A到平面PCD的距离d=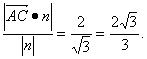
4.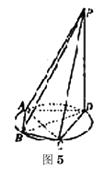 (广东18)(本小题满分14分)
(广东18)(本小题满分14分)
如图5所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
(1)求线段PD的长;
(2)若PC=![]() R,求三棱锥P-ABC的体积.
R,求三棱锥P-ABC的体积.
解:(1)![]() BD是圆的直径
BD是圆的直径
![]()
![]() 又
又 ![]() ,
,
![]()
![]() ,
,  ;
;
(2 ) 在![]() 中,
中,![]()
![]()
![]()
![]()
![]() 又
又 ![]()
![]()
![]() 底面ABCD
底面ABCD
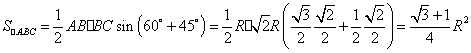
三棱锥![]() 的体积为
的体积为
![]() .
.
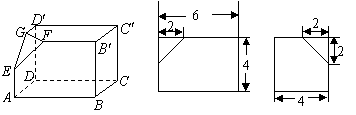
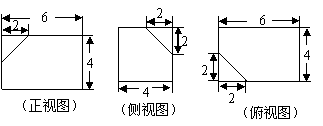
5.(宁夏18)(本小题满分12分)
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图.它的正视图和俯视图在下面画出(单位:cm)
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连结![]() ,证明:
,证明:![]() 面
面![]() .
.

解:(Ⅰ)如图

···················································································· 3分
(Ⅱ)所求多面体体积
![]()
![]()
![]() .··································································· 7分
.··································································· 7分
(Ⅲ)证明:在长方体![]() 中,
中,
连结![]() ,则
,则![]() .
.
因为![]() 分别为
分别为![]() ,
,![]() 中点,
中点,
所以![]() ,
,
从而![]() .又
.又![]() 平面
平面![]() ,
,
所以![]() 面
面![]() . 12分
. 12分
6.(江苏16)(14分)
在四面体![]() 中,
中,![]() ,且E、F分别是AB、BD的中点,
,且E、F分别是AB、BD的中点,
求证:(1)直线EF//面ACD
(2)面EFC⊥面BCD
【解析】:本小题考查空间直线于平面、平面与平面的位置关系的判定,
考查空间想象能力、推理论证能力。
(1)∵E、F分别是AB、BD的中点 ∴EF是△ABD的中位线∴EF//AD
 又∵
又∵![]() 面ACD,AD
面ACD,AD![]() 面ACD∴直线EF//面ACD
面ACD∴直线EF//面ACD
![]() (2)
(2)![]()
![]()

![]()
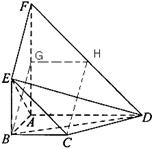
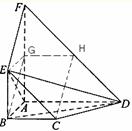
 7.(江西20)如图,正三棱锥
7.(江西20)如图,正三棱锥![]() 的三条侧棱
的三条侧棱![]() 、
、![]() 、
、![]() 两两垂直,且长度均为2.
两两垂直,且长度均为2.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 是
是![]() 的中点,过
的中点,过![]() 的平面与侧棱
的平面与侧棱![]() 、
、![]() 、
、![]() 或其延长线分别相交于
或其延长线分别相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1)求证:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
解
:(1)证明:依题设,![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ∥
∥![]() ,
,
则![]() ∥平面
∥平面![]() ,所以
,所以![]() ∥
∥![]() 。
。
又![]() 是
是![]() 的中点,所以
的中点,所以![]() ⊥
⊥![]() ,
,
则![]() ⊥
⊥![]() 。
。
 因为
因为![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
所以![]() ⊥面
⊥面![]() ,则
,则![]() ⊥
⊥![]() ,
,
因此![]() ⊥面
⊥面![]() 。
。
(2)作![]() ⊥
⊥![]() 于
于![]() ,连
,连![]() 。
。
因为![]() ⊥平面
⊥平面![]() ,
,
根据三垂线定理知,![]() ⊥
⊥![]() ,
,
![]() 就是二面角
就是二面角![]() 的平面角。
的平面角。
作![]() ⊥
⊥![]() 于
于![]() ,则
,则![]() ∥
∥![]() ,则
,则![]() 是
是![]() 的中点,则
的中点,则![]() 。
。
设![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,
,
在![]() 中,
中,![]() ,则,
,则,![]() 。
。
所以![]() ,故二面角
,故二面角![]() 为
为![]() 。
。
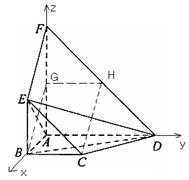
解法二:(1)以直线![]() 分别为
分别为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,![]() 则
则
![]()
所以![]()
所以![]()
所以![]() 平面
平面![]()
由![]() ∥
∥![]() 得
得![]() ∥
∥![]() ,故:
,故:![]() 平面
平面![]()
(2)由已知![]() 设
设![]()
则![]()
 由
由![]() 与
与![]() 共线得:存在
共线得:存在![]() 有
有![]() 得
得
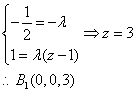
同理:![]()
![]()
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则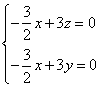 令
令![]() 得
得![]()
![]()
又![]() 是平面
是平面![]() 的一个法量
的一个法量
![]()
所以二面角的大小为![]()
8.(江苏选修)记动点P是棱长为1的正方体![]() 的对角线
的对角线![]() 上一点,记
上一点,记![]() .当
.当![]() 为钝角时,求
为钝角时,求![]() 的取值范围.
的取值范围.
 解:由题设可知,以
解:由题设可知,以![]() 、
、![]() 、
、![]() 为单位正交基底,建立如图所示的空间直角坐标系
为单位正交基底,建立如图所示的空间直角坐标系![]() ,则有
,则有![]() ,
,![]() ,
,![]() ,
,![]()
由![]() ,得
,得![]() ,所以
,所以![]()
![]()
显然![]() 不是平角,所以
不是平角,所以![]() 为钝角等价于
为钝角等价于
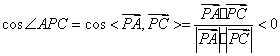 ,则等价于
,则等价于![]()
即 ![]() ,得
,得![]()
因此,![]() 的取值范围是
的取值范围是![]()
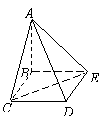
9.(湖南18)(本小题满分12分)
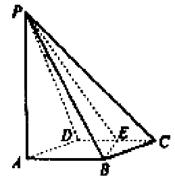 如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=
如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=![]() .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A-BE-P的大小.
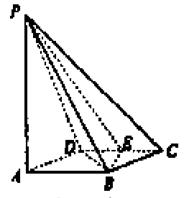 解 解法一(Ⅰ)如图年示,连结BD,由ABCD是菱形且∠BCD=60°知,ΔBCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,所以BE⊥AB.又因为PA⊥平面ABCD,BE
解 解法一(Ⅰ)如图年示,连结BD,由ABCD是菱形且∠BCD=60°知,ΔBCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,所以BE⊥AB.又因为PA⊥平面ABCD,BE![]() 平面ABCD,所以PA⊥BE.而PA∩AB=A,因此BE⊥平面PAB.
平面ABCD,所以PA⊥BE.而PA∩AB=A,因此BE⊥平面PAB.
又BE![]() 平面PBE,所以平面PBE⊥平面PAB.
平面PBE,所以平面PBE⊥平面PAB.
(Ⅱ)由(Ⅰ)知,BE⊥平面PAB,PB![]() 平面PAB,所以PB⊥BE.
平面PAB,所以PB⊥BE.
又AB⊥BE,所以∠PBA是二面角A-BE-P的平面角.
在RtΔPAB中,tan∠PBA=![]() ,∠PBA=60°.
,∠PBA=60°.
故二面角A-BE-P的大小是60°.
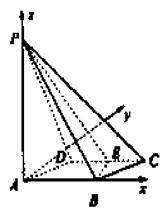 解法二 如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),C(
解法二 如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),C(![]() ),D(
),D(![]() ),P(
),P(![]() ),E(
),E(![]() ).
).
(Ⅰ)因为![]() ,平面PAB的一个法向量是
,平面PAB的一个法向量是![]() =(0,1,0),所以
=(0,1,0),所以![]() 和
和![]() 共线.从而BE⊥平面PAB.又因为BE
共线.从而BE⊥平面PAB.又因为BE![]() 平面BEF,所以平面PBE⊥平面PAB.
平面BEF,所以平面PBE⊥平面PAB.
(Ⅱ)易知![]() =(1,0,-
=(1,0,-![]() ),
), ![]() =(0,
=(0,![]()
![]() ,0),
,0),
设![]() =(x1,y1,z1)是平面PBE的一个法向量,则有
=(x1,y1,z1)是平面PBE的一个法向量,则有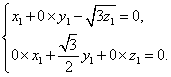
所以y1=0,x1=![]() z1.故可取
z1.故可取![]() =(
=(![]() ,0,1).
,0,1).
而平面ABE的一个法向量是![]() =(0,0,1).
=(0,0,1).
于是,cos<![]() ,
,![]() >=
>=![]() .
.
故二面角A-BE-P的大小是![]()
10.(辽宁19)(本小题满分12分)
 如图,在棱长为1的正方体
如图,在棱长为1的正方体![]() 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥![]() ,截面PQGH∥
,截面PQGH∥![]() .
.
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,
并求出这个值;
(Ⅲ)若![]() ,求
,求![]() 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.
解法一:
(Ⅰ)证明:在正方体中,![]() ,
,![]() ,
,
又由已知可得
![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
所以平面![]() 和平面
和平面![]() 互相垂直.·································································· 4分
互相垂直.·································································· 4分
(Ⅱ)证明:由(Ⅰ)知
![]() ,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
![]() ,是定值.······································································ 8分
,是定值.······································································ 8分
(Ⅲ)解:设![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,
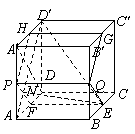 因为
因为![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() ,所以
,所以![]() 分别为
分别为![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.
可知![]() ,
,![]() .
.
所以 .················································································ 12分
.················································································ 12分
解法二:
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz.由已知得![]() ,故
,故
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:在所建立的坐标系中,可得
![]() ,
,
![]() ,
,
![]() .
.
因为![]() ,所以
,所以![]() 是平面PQEF的法向量.
是平面PQEF的法向量.
因为![]() ,所以
,所以![]() 是平面PQGH的法向量.
是平面PQGH的法向量.
因为![]() ,所以
,所以![]() ,
,
所以平面PQEF和平面PQGH互相垂直.····································································· 4分
(Ⅱ)证明:因为![]() ,所以
,所以![]() ,又
,又![]() ,所以PQEF为矩形,同理PQGH为矩形.
,所以PQEF为矩形,同理PQGH为矩形.
在所建立的坐标系中可求得![]() ,
,![]() ,
,
所以![]() ,又
,又![]() ,
,
所以截面PQEF和截面PQGH面积之和为![]() ,是定值.············································· 8分
,是定值.············································· 8分
(Ⅲ)解:由(Ⅰ)知![]() 是平面
是平面![]() 的法向量.
的法向量.
由![]() 为
为![]() 中点可知,
中点可知,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.
所以![]() ,
,![]() ,因此
,因此![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于
![]() . 12分
. 12分
11.(全国Ⅰ18)(本小题满分12分)
四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ;
;
 (Ⅱ)设侧面
(Ⅱ)设侧面![]() 为等边三角形,求二面角
为等边三角形,求二面角![]() 的大小.
的大小.
解:(1)取![]() 中点
中点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
又面![]() 面
面![]() ,
,
![]()
![]() 面
面![]() ,
,
![]()
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 面
面![]() ,
,
![]() .
.
(2)在面![]() 内过
内过![]() 点做
点做![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 面
面![]() ,
,
![]() ,
,
则![]() 即为所求二面角.
即为所求二面角.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
则![]() ,
,
 .
.
12.(全国Ⅱ20)(本小题满分12分)
如图,正四棱柱![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上且
上且![]() .
.
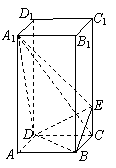 (Ⅰ)证明:
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解法一:
依题设,![]() ,
,![]() .
.
(Ⅰ)连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
由三垂线定理知,![]() .···················································································· 3分
.···················································································· 3分
在平面![]() 内,连结
内,连结![]() 交
交![]() 于点
于点![]() ,
,
 由于
由于![]() ,
,
故![]() ,
,![]() ,
,
![]() 与
与![]() 互余.
互余.
于是![]() .
.
![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() 都垂直,
都垂直,
所以![]()
![]() 平面
平面![]() .······························································································· 6分
.······························································································· 6分
(Ⅱ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .由三垂线定理知
.由三垂线定理知![]() ,
,
故![]() 是二面角
是二面角![]() 的平面角.································································· 8分
的平面角.································································· 8分
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
![]() .
.
 所以二面角
所以二面角![]() 的大小为
的大小为![]() .·························································· 12分
.·························································· 12分
解法二:
以![]() 为坐标原点,射线
为坐标原点,射线![]() 为
为![]() 轴的正半轴,
轴的正半轴,
建立如图所示直角坐标系![]() .
.
依题设,![]() .
.
![]() ,
,![]() .·································· 3分
.·································· 3分
(Ⅰ)因为![]() ,
,![]() ,
,
故![]() ,
,![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .······························································································· 6分
.······························································································· 6分
(Ⅱ)设向量![]() 是平面
是平面![]() 的法向量,则
的法向量,则
![]() ,
,![]() .
.
故![]() ,
,![]() .
.
令![]() ,则
,则![]() ,
,![]() ,
,![]() .······························································ 9分
.······························································ 9分
![]() 等于二面角
等于二面角![]() 的平面角,
的平面角,
 .
.
所以二面角![]() 的大小为
的大小为![]() .························································· 12分
.························································· 12分
13.(山东19)(本小题满分12分)
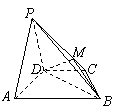 如图,在四棱锥
如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形,已知
是等边三角形,已知![]() ,
,![]() .
.
(Ⅰ)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求四棱锥![]() 的体积.
的体积.
(Ⅰ)证明:在![]() 中,
中,
由于![]() ,
,![]() ,
,![]() ,
,
 所以
所以![]() .
.
故![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() .
.
(Ⅱ)解:过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
由于平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因此![]() 为四棱锥
为四棱锥![]() 的高,
的高,
又![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
因此![]() .
.
在底面四边形![]() 中,
中,![]() ,
,![]() ,
,
所以四边形![]() 是梯形,在
是梯形,在![]() 中,斜边
中,斜边![]() 边上的高为
边上的高为![]() ,
,
此即为梯形![]() 的高,
的高,
所以四边形![]() 的面积为
的面积为![]() .
.
故![]() .
.
14.(上海16)(本题满分12分)
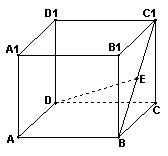 如图,在棱长为2的正方体
如图,在棱长为2的正方体![]() 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
【解】过E作EF⊥BC,交BC于F,连接DF.
∵ EF⊥平面ABCD,
∴ ∠EDF是直线DE与平面ABCD所成的角. ……………4分
由题意,得EF=![]()
 ∵
∵
![]() …………………………..8分
…………………………..8分
∵ EF⊥DF, ∴ ![]() ……………..10分
……………..10分
故直线DE与平面ABCD所成角的大小是![]() ….12分
….12分
15.(四川19)(本小题满分12分)
如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 与
与![]() 都是直角梯形,
都是直角梯形,
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() 分别为
分别为![]() 的中点
的中点
(Ⅰ)证明:四边形![]() 是平行四边形;
是平行四边形;
(Ⅱ)![]() 四点是否共面?为什么?
四点是否共面?为什么?
(Ⅲ)设![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
【解1】:(Ⅰ)由题意知,![]()
 所以
所以![]()
![]()
![]()
又![]()
![]()
![]() ,故
,故![]()
![]()
![]()
所以四边形![]() 是平行四边形。
是平行四边形。
(Ⅱ)![]() 四点共面。理由如下:
四点共面。理由如下:
由![]()
![]()
![]() ,
,![]() 是
是![]() 的中点知,
的中点知,![]()
![]()
![]() ,所以
,所以![]()
由(Ⅰ)知![]() ,所以
,所以![]() ,故
,故![]() 共面。又点
共面。又点![]() 在直线
在直线![]() 上
上
所以![]() 四点共面。
四点共面。
(Ⅲ)连结![]() ,由
,由![]() ,
,![]()
![]()
![]() 及
及![]() 知
知![]() 是正方形
是正方形
故![]() 。由题设知
。由题设知![]() 两两垂直,故
两两垂直,故![]() 平面
平面![]() ,
,
因此![]() 是
是![]() 在平面
在平面![]() 内的射影,根据三垂线定理,
内的射影,根据三垂线定理,![]()
又![]() ,所以
,所以![]() 平面
平面![]()
由(Ⅰ)知![]() ,所以
,所以![]() 平面
平面![]() 。
。
由(Ⅱ)知![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,得平面
,得平面![]() 平面
平面![]()
【解2】:由平面![]() 平面
平面![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,
,
以![]() 为坐标原点,射线
为坐标原点,射线![]() 为
为![]() 轴正半轴,建立如图所示的直角坐标系
轴正半轴,建立如图所示的直角坐标系![]()
(Ⅰ)设![]() ,则由题设得
,则由题设得
![]()
 所以
所以![]()
于是![]()
又点![]() 不在直线
不在直线![]() 上
上
所以四边形![]() 是平行四边形。
是平行四边形。
(Ⅱ)![]() 四点共面。理由如下:
四点共面。理由如下:
由题设知![]() ,所以
,所以
![]() 又
又![]() ,故
,故![]() 四点共面。
四点共面。
(Ⅲ)由![]() 得,所以
得,所以![]()
又![]() ,因此
,因此![]()
即![]()
又![]() ,所以
,所以![]() 平面
平面![]()
故由![]() 平面
平面![]() ,得平面
,得平面![]() 平面
平面![]()
16.(天津19)(本小题满分12分)
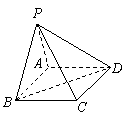 如图,在四棱锥
如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形.已知
是矩形.已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明![]() 平面
平面![]() ;
;
(Ⅱ)求异面直线![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角![]() 的大小.
的大小.
(Ⅰ)证明:在![]() 中,由题设
中,由题设![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,于是
,于是![]() .在矩形
.在矩形![]() 中,
中,![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)解:由题设,![]() ,所以
,所以![]() (或其补角)是异面直线
(或其补角)是异面直线![]() 与
与![]() 所成的角.
所成的角.
在![]() 中,由余弦定理得
中,由余弦定理得
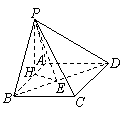
![]() .
.
由(Ⅰ)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,因而
,因而![]() ,于是
,于是![]() 是直角三角形,
是直角三角形,
故![]() .
.
所以异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() .
.
(Ⅲ)解:过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连结
,连结![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .又
.又![]() ,因而
,因而![]() 平面
平面![]() ,故
,故![]() 为
为![]() 在平面
在平面![]() 内的射影.由三垂线定理可知,
内的射影.由三垂线定理可知,![]() .从而
.从而![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由题设可得,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
于是在![]() 中,
中,![]() .
.
所以二面角![]() 的大小为
的大小为![]() .
.
17.(浙江20)(本题14分)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,![]() BCF=
BCF=![]() CEF=
CEF=![]() ,AD=
,AD=![]() ,EF=2。
,EF=2。
 (Ⅰ)求证:AE//平面DCF;
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为![]() ?
?
方法一:
 (Ⅰ)证明:过点
(Ⅰ)证明:过点![]() 作
作![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
可得四边形![]() 为矩形,
为矩形,
又![]() 为矩形,
为矩形,
所以![]() ,从而四边形
,从而四边形![]() 为平行四边形,
为平行四边形,
故![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() .
.
由平面![]() 平面
平面![]() ,
,![]() ,得
,得
![]() 平面
平面![]() ,
,
从而![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,因为
中,因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() ,
,
从而![]() .
.
于是![]() .
.
因为![]() ,
,
所以当![]() 为
为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
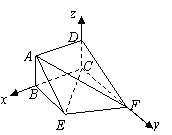 方法二:如图,以点
方法二:如图,以点![]() 为坐标原点,以
为坐标原点,以![]() 和
和![]() 分别作为
分别作为![]() 轴,
轴,![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,从而
,从而![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
故![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,从而
,从而
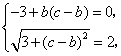
解得![]() .
.
所以![]() ,
,![]() .
.
设![]() 与平面
与平面![]() 垂直,
垂直,
则![]() ,
,![]() ,
,
解得![]() .
.
又因为![]() 平面
平面![]() ,
,![]() ,
,
所以![]() ,
,
得到![]() .
.
所以当![]() 为
为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
18.(重庆20)(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
如图(20)图,
![]() 为平面,
为平面,![]() AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角![]() 的大小为
的大小为![]() ,求:
,求:
(Ⅰ)点B到平面![]() 的距离;
的距离;
(Ⅱ)异面直线l与AB所成的角(用反三角函数表示).
解:(1)如答(20)图,过点B′C∥A′A且使B′C=A′A.过点B作BD⊥CB′,交CB′的延长线于D.
由已知AA′⊥l,可得DB′⊥l,又已知BB′⊥l,故l⊥平面BB′D,得BD⊥l又因BD⊥CB′,从而BD⊥平面α,BD之长即为点B到平面α的距离.
因B′C⊥l且BB′⊥l,故∠BB′C为二面角α-l-β的平面角.由题意,∠BB′C=
![]() .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=![]() ,BD=BB′·sinBB′D
,BD=BB′·sinBB′D
=![]() .
.
(Ⅱ)连接AC、BC.因B′C∥A′A,B′C=A′A,AA′⊥l,知A′ACB′为矩形,故AC∥l.所以∠BAC或其补角为异面直线l与AB所成的角.
在△BB′C中,B′B=2,B′C=3,∠BB′C=![]() ,则由余弦定理,
,则由余弦定理,
BC=![]() .
.
因BD![]() 平面
平面![]()
![]() ,且DC
,且DC![]() CA,由三策划线定理知AC
CA,由三策划线定理知AC![]() BC.
BC.
故在△ABC中,∠BCA=![]() ,sinBAC=
,sinBAC=![]() .
.
因此,异面直线l与AB所成的角为arcsin![]() .
.
19.(湖北18).(本小题满分12分)
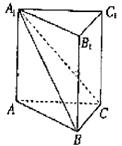 如图,在直三棱柱
如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]()
(Ⅰ)求证: ![]()
(Ⅱ)若![]() ,直线AC与平面
,直线AC与平面![]() 所成的角为
所成的角为![]() ,二面角
,二面角![]()
![]()
![]()
(Ⅰ)证明:如右图,过点A在平面A1ABB1内作AD⊥A1B于D,则
由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
 得AD⊥平面
得AD⊥平面
A1BC.又BC![]() 平面A1BC
平面A1BC
所以AD⊥BC.
因为三棱柱ABC-A1B1C1是直三棱柱,
则AA1⊥底面ABC,所以AA1⊥BC.
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB![]() 侧面A1ABB1,
侧面A1ABB1,
故AB⊥BC.
(Ⅱ)证法1:连接CD,则由(Ⅰ)知∠ACD就是直线AC与平面A1BC所成的角,∠ABA1就是二面角A1-BC-A的颊角,即∠ACD=θ,∠ABA1=j.
于是在RtΔADC中,sinθ=![]() ,在RtΔADA1中,sin∠AA1D=
,在RtΔADA1中,sin∠AA1D=![]() ,
,
∴sinθ=sin∠AA1D,由于θ与∠AA1D都是锐角,所以θ=∠AA1D.
又由RtΔA1AB知,∠AA1D+j=∠AA1B+j=![]() ,故θ+j=
,故θ+j=![]() .
.
证法2:由(Ⅰ)知,以点B为坐标原点,以BC、BA、BB1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
设AB=c(c<a=,则B(0,0,0),A(0,c,0),C(![]() ),
),
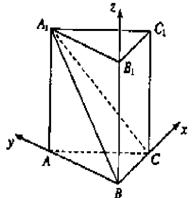 A1(0,c,a),于是
A1(0,c,a),于是![]() ,
,![]() =(0,c,a),
=(0,c,a),
![]() ,
,![]() =(0,c,a)
=(0,c,a)
设平面A1BC的一个法向量为n=(x,y,z),
则由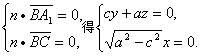
可取n=(0,-a,c),于是
n·![]() =ac>0,
=ac>0,![]() 与n的夹角b为锐角,则b与q互为余角.
与n的夹角b为锐角,则b与q互为余角.
sinq=cosb=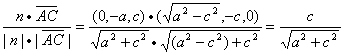 ,
,
cosj=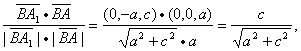
所以sinq=cosj=sin(![]() ),又0<q,j<
),又0<q,j<![]() ,所以q+j=
,所以q+j=![]() .
.
20.(陕西19)(本小题满分12分)
三棱锥被平行于底面![]() 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
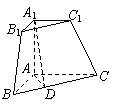 (Ⅰ)证明:平面
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解法一:(Ⅰ)![]()
![]() 平面
平面![]() 平面
平面![]() ,
,
![]()
![]() .在
.在![]() 中,
中,![]() ,
,![]() 为
为![]() 中点
中点
![]()
![]() .又
.又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() .
.
(Ⅱ)如图,作![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,
,
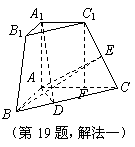 由已知得
由已知得![]() 平面
平面![]() .
.
![]() 是
是![]() 在面
在面![]() 内的射影.
内的射影.
由三垂线定理知![]() ,
,
![]() 为二面角
为二面角![]() 的平面角.
的平面角.
过![]() 作
作![]() 交
交![]() 于
于![]() 点,
点,
则![]() ,
,![]() ,
,
![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
![]() ,
,
即二面角![]() 为
为![]() .
.
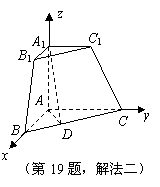
解法二:(Ⅰ)如图,建立空间直角坐标系,
则![]() ,
,
![]()
![]() 为
为![]() 中点,
中点,![]() 点坐标为
点坐标为![]() .
.
![]()
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)![]() 平面
平面![]() ,如图可取
,如图可取![]() 为平面
为平面![]() 的法向量,
的法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() .
.
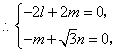
![]() ,
,
如图,令![]() ,则
,则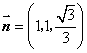 ,
,
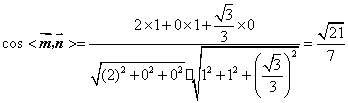 ,
,
即二面角![]() 为
为![]() 为所求.
为所求.
