08届高考数学第二次联考试卷

数 学 试 题

第Ⅰ卷（选择题　共50分）

一、选择题（本题共10小题，每小题5分，共50分. 每小题给出的四个选项中，只有一项是符合题目要求的）

1．集合等于（　　）

　　　 A．　　　　　B．　　　　 C．　　D．

2．△ABC中，“A>30°”是“”的　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）　

A．充分不必要　　　　　　　　　　　　　　　　　　　　B．必要不充分　　　　

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

3．已知的最大值是　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．11　　　　　　　　　　　B．9　　　　　　　　　　　　C．5　　　　　　　　　　　　D．3

4．（理）已知数列{a_n}是等比数列，若S₃=18，S₄－a₁=－9，S_n为它的前n项和，则等于（　　）

　　　 A．48　　　　　　　　　　　B．32　　　　　　　　　　　C．16　　　　　　　　　　　D．8

 （文）在各项都为正数的等比数列{a_n}中，首项a₁=3，前三项和为21，则a₃+a₄+a₅等于（　　）

　　　 A．33　　　　　　　　　　　B．72　　　　　　　　　　　C．84　　　　　　　　　　　D．189

5．函数的反函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　 B．　　　

　　　 C．　　　　　　　　　　D．　　　　　

6．将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里球的个数不小于该盒子的编号，则不同的放法有　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．10种　　　　　　　　　B．20种　　　　　　　　　C．30种　　　　　　　　 D．52种

7．定义在R上的偶函数时单调递增，则（　　）

　　　 A．　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　 D．

8．已知，且关于x的函数在R上有极值，则与的夹角范围为　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　B．　　　　　　　 C．　　　　　　　D．

9．如果以原点为圆心的圆经过双曲线的焦点，而且被该双曲线的右准线分成弧长为2:1的两段圆弧，那么该双曲线的离心离e等于　　　 （　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　　D．

10．已知C为线段AB上一点，P为直线AB外一点，满足，

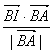　　，I为线段PC上一点，且有，则的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　  ）

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．　　　　　　　　　　D．－1

二、填空题（本题共6小题，每小题4分，共24分，将答案写在题中横线上）

11．（理）复数的虚部为　　　　　　　 

　 （文）某校有老师200人，男学生1200，女学生1000人，现用分层抽样的方法从所有老师中抽取一个容量的n的样本；已知从女学生中抽取的人数为80人，则n=　　　　

12．的展开式中，常数项为　　　　　　　 

13．设点（m，n）在直线x+y=1位于第一象限内的图象上运动，则的最大值是　　　　

14．已知，且的两个根，则　　　　 

15．过抛物线的焦点F的直线l的倾斜角交抛物线于A，B两点，且A点在x轴上方，则AF的取值范围是　　　　　　 

16．（理）数列由下列条件所确定： 满足如下条件：当，当

　　.

　　那么，当的通项公式

　　时，用a₁，b₁表示{b_k}的通项公式b_k=　　　　 （k=2，3，…，n）

　 （文）数列{a_n}满足递推式为等差数列的实数=　　　　　 

三、解答题（本大题共6小题，满分76分）

17．（本小题满分12分）

　　已知函数的最小正周期为.

　 （1）求的单调递增区间；

　 （2）在△ABC中，角A，B，C的对边分别是a，b，c满足，求函数的取值范围.

18．（本小题满分12分）

　 （理）一个小正方体的六个面，三个面上标以数字0. 两个面上标以数字1，一个面上标

以数字2，（1）甲、乙两人各抛掷一次，谁的点数大谁就胜，求甲获胜的概率；（2）将这个小正方体抛掷两次，用变量ξ表示向上点数之积，求随机变量ξ的概率分布列及数学期望Eξ.

　 （文）甲、乙两人各进行3次投篮，甲每次投中的概率为，乙每次投中的概率为，求：（1）甲恰好投中2次的概率；（2）乙至少投中2次的概率；（3）甲、乙两人共投中5次的概率.

19．（本小题满分12分）

　　已知数列{a_n}，S_n是其前n项和，且，（1）求数列{a_n}

的通项公式；（2）设是数列{b_n}的前n项和，求使得对所有都成立的最小正整数m.

20．（本小题满分12分）

　 （理）已知函数，在x=1处取得极值2，（1）求函数的解析式；（2）m满足什么条件时，区间（m，2m+1）为函数的单调增区间；（3）若为图象上的任意一点，直线l与的图象切于P点，求直线l的倾斜角的取范围.

　 （文）已知函数，求曲线的平行于直线的切线方程；（2）若函数在区间[－2，2]上有最大值3，求常数m的值及此函数的最小值.

21．（本小题满分14分）

已知椭圆C的方程是，斜率为1的直线l与椭圆C交于两点. （1）若椭圆的离心率，直线l过点M（b，0），且，求椭圆的方程；（2）直线l过椭圆的右焦点F，设向量，若点P在椭圆C上，求的取值范围.

22．（本小题满分14分）

已知函数平移后得到的图象关于原点对称，

　 （1）求a，b，c的值；（2）设；

　 （理科学生）（3）设x是正实数，求证：

08届高考数学第二次联考试卷

数学试题参考答案

1．D　2． B　3．A　 4．（理）C（文）C　 5．B　 6．A　 7．B　 8．C　 9．D　 10．D

11．（理）　（文）192　　12．672　 13．－2　 14．　 15．

16．（理）　（文）

17．（1） …………2分

∵　…………4分

∴的单调递增区间为　…………6分

（2）∵

∴　…………8分

 ……10分

∵

∴　　…………12分

18．（理）（1）面上是数字0的概率为，数字为1的概率为，数字为2的概率…2分

当甲掷出的数字为1，乙掷出的数字为0时，甲获胜的概率为

当甲掷出的数字为2，乙掷出的数字为0或1时，甲获胜的概率为

∴甲获胜的概率为 　　……………………6分

（2）ξ的取值为0、1、2、4

∴随机变量ξ的概率分布列为

ξ	0	1	2	4
P

　　　　　　  ……………………10分

∴Eξ=　 ……………………12分

　 （文）（1）甲恰好投中2次的概率为　 …………3分

（2）乙至少投中2次的概率为　　 ……7分

（3）设甲、乙两人共投中5次为事件A，甲恰投中3次且乙恰投中2次的事件B₁，

甲恰投中2次且乙恰投中3次为事件B₂，则A=B₁+B₂，B₁、B₂为互斥事件

　 ……11分

∴　 ………………12分

19．（1）∵

∴　 …………2分

又a₁=2　 ∴　……4分

∴{a_n}是一个以2为首项，8为公比的等比数列

∴　 ………………6分

（2） ……8分

∴　…………10分

∴∴最小正整数m=7　…………12分

20．（理）（1）已知函数　…………2分

又∵在x=1处取得极值2，　∴

解得　　　…………4分

（2）由得：，∴函数的单调递增区间为（－1，1）……6分

若（m，2m+1）为单调增区间，则有 ……8分

（3）

∴直线l的斜率为  ……10分

令，则直线l的斜率　

∴　 ∴倾斜角的取值范围是　 ……12分

（文）（1），设所求切线的切点为，

则其斜率为　…………3分

当时切点为（3，0）， ∴切线方程为y=18x－54

当时切点为（－1，－8）， ∴切线方程为y=18x+10　…………5分

（2）令　 …………6分

	－2	（－2，0）	0	（0，2）	2
		+	0	－	0
	m－40	增函数	m	减函数	m－8

　 ………………………………10分　　

由此可知　

　 …………12分

21．（1）∵

，

即

根据　，

所以椭圆方程为　　　………………6分

（2）由

据韦达定理可得： 　……8分

因为P在椭圆上，　 ，

 …………11分

∵

∴……14分

22．（1）函数的图象按 平移后得到的图象的函数式为

∵其函数图象关于原点对称， ∴为奇函数，

∴

即　，　∵

0　 ………………3分

又∵①，又②

由①②及　 ………………5分

（2），

当且仅当时，取等号

但　…………7分

，

当

∴ ……9分

（3）

　 ………………10分

令

∴

　…………13分

　 ………………14分