专题考案(4)向量板块 第2课 向量的数量积

(时间：90分钟　满分：100分)

题型示例

已知a=3,b=2,a与b的夹角为120°，问k为何值时，两向量ka-b与a+2b互相垂直?

解　设a=(3,0),则b=(2cos120°,2sin120°)=(-1,).

于是ka-b=(3k+1,-),a+2b=(1,2).

∵(ka-b)⊥(a+2b),∴(3k+1)×1+(-)×2·=0.解得k=.

∴当k=时，向量ka-b与a+2b互相垂直.

点评　向量的坐标运算并不一定非要题目事先给定坐标，只要不失一般性，完全可以像本题那样“构造”坐标.强化向量的坐标运算意识，可以帮助我们把一个抽象问题迅速具体化.其实，向量的坐标运算提供了一种把其他运算转化为纯数学运算的有力途径，尤其是碰到几何问题时.

一、选择题 (7×3′＝21′)

1．已知a,b,c为非零的平面向量，甲：a·b=a·c,乙：b=c，则　　　　　　　　  (　　)

A.甲是乙的充分条件但不是必要条件

B.甲是乙的必要条件但不是充分条件

C.甲是乙的充要条件

D.甲既不是乙的充分条件也不是乙的必要条件

2．已知a,b均为单位向量，它们的夹角为60°,那么a+3b等于　　　　　　　　 (　　)

A.　　　　 B.　　　　 C.　　　　 D.4

3．在ABCD中,AC=,BD=,周长为18,则这个平行四边形的面积为　　　 (　　)

A.16 　　　　B.17　　　　 C.18　　　　 D.32

4．若向量a与b的夹角为60°,b=4,(a+2b)·(a-3b)=-72.则向量a的模是　　　  (　　)

A.2　　　　  B.4　　　　  C.6　　　　  D.12

5．下列各向量中，与a＝(3,2)垂直的向量是　　　　　　　　　　　　　　　　 (　　)

A.b=(3，－2)　　 B.b=(2,3)　　 C.b=(-4,6)　　 D.b=(-3,2)

6．已知a⊥b,a=2,b=3,且3a+2b与λa-b垂直，则λ等于　　　　　　　　　　 (　　)

A.　 　　　B.-　　　　 C.±　　　　 D.1

7．已知m,n是夹角为60°的两个单位向量，则a=2m+n和b=-3m+2n的夹角是　(　　)

A.30°　　　　B.60°　　　  C.120°　　　  D.150°

二、填空题(5×3′＝15′)

8．已知A(1，3)、B(2，4)、C(5，6)，则=　　　　  .

9．已知=0，的夹角为　　　　 .

10．已知e为单位向量，a=4,a与e的夹角为π，则a在e方向上的投影是　　　 .

11．已知a=(4,3),b=(-1,2),则a与b的夹角为　　　　 .

12．平面向量a,b中，已知a=(4,-3),b=1,且a·b=5,则向量b=　　　 　 .

三、解答题(4×10′＝40′)

13．已知a=4,b=5,当

(1)a∥b;

(2)a⊥b;

(3)a与b的夹角为60°时，分别求a与b的数量积.

14．求证:三角形ABC的三条高线AD、BE、CF交于一点H.

15．已知向量a=(1,1),b=(1,0),c满足a·c=0且a=c,b·c>0.

(1)求向量c;

(2)若映射f:(x,y)→(x₁,y₁)=xa+yc,求映射f下(1,2)的原象.

16．设O是△ABC的外心，H是三角形内一点，且,求证：H是△ABC的垂心.

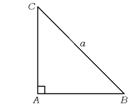四、思考与讨论(2×12′＝24′)

17．已知a=(,-1),b=().

(1)若存在不同时为零的实数k和t,使x=4a+(t²-3)b,y=-ka+tb，且x⊥y，

求k=f(t)的解析式；

图1

(2)确定f(t)的单调区间．

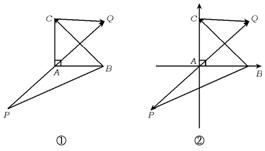
18．如图1，在Rt△ABC中，已知BC=a,若长为2a的线段PQ以点A

为中点，问的夹角θ取何值时的值最大？并求出这个最大值.

参考答案

1．B　a·b=a·ca·(b-c)=0a与(b-c)垂直，或b-c=0.故甲乙，反过来，若b=ca·b=a·c，即乙甲，故甲是乙的必要非充分条件.

2．C　a+3b²=(a+3b)²=a²+6a·b+9b²=a²+6abcos〈a,b〉+9b²,

∵a=1,b=1,〈a,b〉=60°,∴原式=1+6×1×1×cos60°+9=13,∴a+3b=.

3．A　∵2=9，

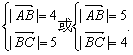
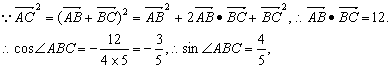
∴=4×5×

4．C　(a+2b)·(a-3b)=a²-a·b-6b²=-72,∴a²-a·b·cos60°-6b²=-72.

∴b=4代入上式，解得:a=6(∵a>0).

5．C　验证a·b=0即可.

6．A　(3a+2b)(λa-b)=0,又a·b=0,∴3λa²-2b²=03λ×4-2×9=0λ=.

7．C　不妨设m=(1,0),n=(,),则a=(,),b=(-2,),

a=,b=,a·b=-5+∴cosθ=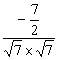=-，故θ=120°．

8．25　=(1,1),=(4,3),=(3,2)，∴·+·=(1×4+1×3)+(4×3+3×2)=25.

9．120°　∵²=+²=²+²+2·cosθ,∴cos=-,θ=120°.

10．-2　4×cosπ=4×(-)=-2为所求.

11．arccos　cos〈a,b〉==.

12．　设b=(x,y),由已知

13．解　(1)a∥b时，有两种情况.

若a与b同向，则θ=0°，a·b=a·b=20；

若a与b反向，则θ=180°，a·b=-a·b=-20.

(2)当a⊥b时，θ=90°，∴a·b=0.

(3)当a与b夹角为60°时，a·b=a·bcos60°=10.

14．分析　要证三条高线交于一点，只要证两条高线的交点在第三条高线上.

证明　设BE与CF交于H,并设=a,=b,=h,

则=b-a,=h-a,=h-b

∵,∴(h-a)·b=0　　　　　　　　　　　　　　　　　　　　　　　　 ①

∵,∴(h-b)·a=0　　　　　　　　　　　　　　　　　　　　　　　　 ②

∵(h-a)·b=(h-b)·a，∴h·b=h·a,即h·(b-a)=0.

∴,即H在AD上.故AD、BE、CF交于一点H.

点评　用向量作工具解几何问题总是先得一些向量为已知的，再用这些向量表示其他向量，并建立相应关系式，至于选用哪些为基本向量，则应根据实际情况而定.

15．解　（1）设c=(m,n),由题意得m+n=0,且m²+n²=2且m·1+n·0>0.

解之得m=1,n=-1,∴c=(1,-1).

(2)由题意得x(1,1)+y(1,-1)=(1,2),∴x+y=1且x-y=2,解之得x=,y=-.

∴(1,2)的原象是(-).

16．证明　∵

同理得，.

所以H是△ABC的垂心.

点评　处理垂直、夹角和距离是两个向量数量积的强项，这也是学习向量的主要目的之一.

17．解　(1)由已知a·b=0,又x⊥y，且x,y不同时为零．

∴x·y=［4a+(t²-3)b］·［-ka+tb］=0.∴-4k+(t³-3t)=0,∴k=(t³-3t)(t≠0).

(2)f(t)=(t³-3t)，∵f(t¹)-f(t²)=(t¹-t²)(-3)，

当t¹<t²≤-1时，f(t¹)-f(t²)<0．

当-1≤t¹<t²≤1时，f(t¹)-f(t²)>0．

当1≤t¹<t²时，f(t¹)-f(t²)<0.

∴f(t)在(-∞，-1)上为增函数，在［-1,1］上为减函数，在［1,+∞］上为增函数．

18．分析　本题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力.

解　方法1　如图2①.∵⊥,∴·=0.

∵=-,=-,=-,∴·=(-)·(-)

=·-·-·+·=-a²-·+·

=-a²-·(-)=-a²+·=-a²+a²cosθ.

故当cosθ=1,即θ=0(与方向相同)时，·最大，其最大值为0.

	图2

方法2　以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图D19②所示的平面直角坐标系.

设AB=c.AC=b,则A(0,0),B(c,0),C(0,b),且｜PQ｜=2a,BC=a.

设点P的坐标为（x,y）,则Q（-x,-y），∴=(x-c,y),=(-x,-y-b),=(-c,b),=(-2x,-2y).

∴·=(x-c)(-x)+y(-y-b)=-(x²+y²)+cx-by.

∵cosθ=,∴cx-by=a²cosθ.∴·=-a²+a²cosθ.

故当cosθ=1,即θ=0(与方向相同)时，·最大，其最大值为0.

点评　题型新颖，培养了学生的知识迁移能力，及运算化简能力.