08届高三数学上学期教学调研测试

数　　学 2008.1

一填空题(本大题共14小题,每小题5分,共70分)

1.设集合集合则= 　  ▲　　 .

2.函数的最小正周期是　　　 ▲　　　 .

3.计算  　　▲　 　  

4.函数的图象关于直线对称.则 　　　▲　　

5.命题“”的否定是　　　　▲　　　　 

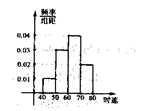
6.右图为80辆汽车通过某一段公路时的时速的频率分布直方图,

则时速在的汽车大约有 　 ▲　　 辆.

7.把一根匀均匀木棒随机地按任意点拆成两段,则“其中一段的长

度大于另一段长度的2倍”的概率为　　　▲　　　　　　

8．函数在上的单调递增区间为 　　▲　　  

9．圆上一点到直线的距离的最小值为 　▲   

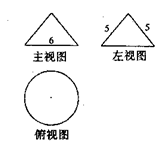
10．一个几何体的三视图及其尺寸如右图所示（单位：cm），则该几何体的体积是  ▲  cm³.

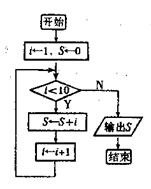
11.一个算法的流程图如图所示，则输出S为 　　▲　 　　　

12．已知向量a,b,c满足：c=a+b,且c⊥a,则a与b的夹角大小是 　 ▲　  

13．已知当mn取得最小值时，直线与曲线的交点个数为 　　 ▲　　　 

14．在计算“”时，某同学学到了如下一种方法：

先改写第k项：由此得

…

相加，得

类比上述方法，请你计算“”，其结果为   ▲　 .

二、解答题（本大题共6小题，共90分，解答时应写出文字说明、证明过程或演算步骤）

15．（本小题满分14分）

在中，角A、B、C的对边分别为，已知向量

且满足，

（Ⅰ）求角A的大小；

（Ⅱ）若试判断的形状。

16．（本小题满分14分）

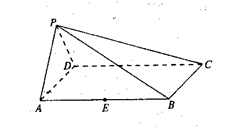
如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，PA=PD，且PD与底面ABCD所成的角为，

（Ⅰ）求证：PA⊥平面PDC；

（Ⅱ）已知E为棱AB的中点，问在棱PD上是否存在一点Q，使EQ∥平面PBC？若存在，写出点Q的位置，并证明你的结论；若不存在，说明理由。

17．（本小题满分15分）

如图，已知椭圆C：的左右焦点分别为F₁、F₂，点B为椭圆与y轴的正半轴的交点，点P在第一象限内且在椭圆上，且PF₂与x轴垂直，

（Ⅰ）求椭圆C的方程；

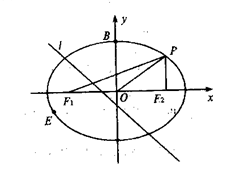（Ⅱ）设点B关于直线的对称点E（异于点B）在椭圆C上，求m的值。

18．（本小题满分15分）

已知直线与圆交于不同点A_n、B_n,其中数列满足：.

（Ⅰ）求数列的通项公式；

（Ⅱ）设求数列的前n项和.

19．（本小题满分16分）

某商店经销一种奥运会纪念品，每件产品的成本为30元，并且每卖出一件产品需向税务部门上交元（为常数，2≤a≤5 ）的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与(e为自然对数的底数)成反比例.已知每件产品的日售价为40元时，日销售量为10件。

（Ⅰ）求该商店的日利润L（x）元与每件产品的日售价x元的函数关系式；

（Ⅱ）当每件产品的日售价为多少元时，该商品的日利润L（x）最大，并求出L（x）的最大值。

20．（本小题满分16分）

已知函数

（Ⅰ）试判断在定义域上的单调性；

（Ⅱ）当时，求证

参考答案

一、填空题

1．{2，3}　 2.　 3.1+i　 4.3　 5.　6.24　7.　8.

9.2　10.　 11. 45　 12.　 　13.2　 14.

二、解答

15．（1）

（2）。

16．（1）略　

（2）存在 当点Q为PD中点时，EQ∥平面PBC

取PC中点证明BEQF为平行四边形即可。

17．（1）椭圆C方程为：，

（2）BE⊥l, BE方程：

由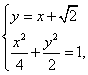得

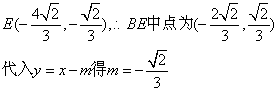
18．（1）圆心到直线的距离，

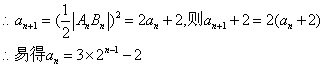
（2）　

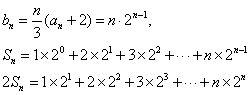
相减得

19．（1）设日销售量为

则日利润

（2）

①当2≤a≤4时，33≤a+31≤35，当35 <x<41时，

∴当x=35时，L（x）取最大值为

②当4＜a≤5时，35≤a+31≤36，

易知当x=a+31时，L（x）取最大值为

综合上得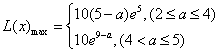

20．（1）

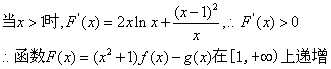
（2）由（1）知

。
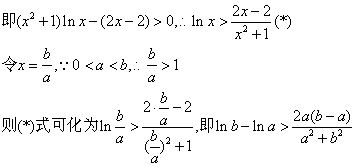