08届高中毕业班理科数学第一次模拟考试
数学试题(理科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
注意事项:
①请把答案按要求填写在答题卡上,否则答题无效。
②考试结束,监考员将答题卡收回,试题卷不收。
参考公式:
如果事件A、B互斥,那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式 ![]() 其中R表示球的半径
其中R表示球的半径
球的体积公式 ![]() 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.诱导公式![]() =( )(其中
=( )(其中![]() ) ( )
) ( )
A.![]() B.
B.![]()
C.![]() D.与n的值为奇偶数有关
D.与n的值为奇偶数有关
2.已知对任意实数x,有![]()
则![]() 时 ( )
时 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.命题“若![]() ”的逆否命题是 ( )
”的逆否命题是 ( )
A.若![]() B.若
B.若![]()
C.若则![]() D.若
D.若![]()
4.等比数列![]() ,则T1,T2,…,Tn中最小的是
,则T1,T2,…,Tn中最小的是
( )
A.T11 B.T10 C.T9 D.T8
5.若![]() 是非零向量且满足:
是非零向量且满足:![]() 的夹角是 ( )
的夹角是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知点P是以F1、F2为焦点的椭圆![]() 上一点,若PF1⊥PF2,
上一点,若PF1⊥PF2,
![]() ,则此椭圆的离心率是 ( )
,则此椭圆的离心率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.二项式![]() 的展开式中含x5的项的系数是 ( )
的展开式中含x5的项的系数是 ( )
A.72 B.—72 C.36 D.—36
8.电视台连续播放5个广告,其中3个不同的商业广告和2个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且2个奥运宣传广告不能连续播放,则不同的播放方式有 ( )
A.120种 B.48种 C.36种 D.18种
9.给出以下四个命题
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线互相平行;
④如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
其中真命题的个数是 ( )
A.4 B.3 C.2 D.1
|
A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
11.一个与球心距离为1的平面,截球所得圆的面积为![]() ,则球的表面积为 ( )
,则球的表面积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.12π
D.12π
12.点P是椭圆![]() 的交点,F1与F2是两曲线的公共焦点,则∠F1PF2= ( )
的交点,F1与F2是两曲线的公共焦点,则∠F1PF2= ( )
A.![]() B.
B.![]() C.
C.![]() D.与a的取值无关
D.与a的取值无关
第Ⅱ卷(非选择题90分)
|
13.已知![]() 的根为
。
的根为
。
|
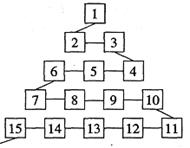
15.右图是从事网络工作者经常用来解释网络运作的
蛇形模型,数字1出现在第1行;数字2、3出现
在第2行;数字6、5、4(从左至右)出现在第3行;
数字7、8、9、10出在第4行;依次类推。试问第
50行,从左至右算,第7个数字为 。
16.下列命题:
(1)若![]() 是定义在[—1,1]上的偶函数,且在[—1,0]上是增函数,
是定义在[—1,1]上的偶函数,且在[—1,0]上是增函数,![]() ;
;
(2)若锐角![]() ;
;
(3)若![]() ;
;
(4)要得到函数![]() 个单位。
个单位。
其中正确命题的个数有 个。
三、解答题(要求写出必要的步骤和运算过程)
17.(本小题满分10分)
角![]() 满足下列条件:
满足下列条件:
(1)![]() ,
,
(2)![]() 的值。
的值。
18.(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数;
![]()
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数![]() 的分布列和数学期望。
的分布列和数学期望。
19.(本小题满分12分)
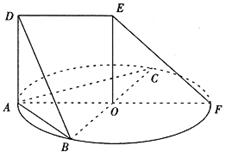
|
(1)求二面角B—AD—F的大小;
(2)求直线BD与EF所成的角。
20.(本小题满分12分)
已知等差数列![]() ,公差大于0,且
,公差大于0,且![]() 的两根,数列
的两根,数列
![]()
(1)写出数列![]() 、{
、{![]() }的通项公式;
}的通项公式;
(2)记![]()
21.(本小题满分12分)
设直线![]() 相交于A、B两个不同的点,与
相交于A、B两个不同的点,与
x轴相交于点F。
(1)证明:![]() ;
;
(2)若F是椭圆的一个焦点,且以AB为直径的圆过原点,求a2。
22.(本小题满分12分)
设函数![]()
(1)求![]() 的单调增区间和单调减区间 ;
的单调增区间和单调减区间 ;
(2)若当![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若关于x的方程![]() 在区间[0,2]上恰有两个相异的实根,求实数a的取值范围。
在区间[0,2]上恰有两个相异的实根,求实数a的取值范围。
参考答案
一、选择题
ACDBBA CCBADB
|
13.2; 14.![]() ; 15.1232; 16.2
; 15.1232; 16.2
三、解答题
17.解:![]() …………4分
…………4分
又![]() …………7分
…………7分
解得:![]() …………10分
…………10分
18.解:(1)计事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,
所以![]() …………4分
…………4分
(2)![]() 可取1,2,3,4。
可取1,2,3,4。
![]() ,
,
![]() ;…………8分
;…………8分
故ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
…………10分
![]()
答:![]() 的数学期望为
的数学期望为![]() …………12分
…………12分
19.解:因为AD⊥平面ABF,而AB、AF![]() 平面ABF
平面ABF
所以AD⊥AB,AD⊥AF
则∠BAF就是二面角B—AD—F的平面角 …………3分
∵AB、BC是⊙O的直径,∴ABFC是矩形
又AB=AC=6,则ABFC是正方形
则∠BAF=45°,
即所求二面角的大小为45° …………6分
(2)由上可知:ABFC是边长为6的正方形,则BC⊥AO
AD⊥平面ABF,则AO是OD在平面ABF上的射影
∴OD⊥BC
又OE∥AD OE=AD 则DE∥AF
DE=AO=OF=OB=![]()
OFED是平行四边形 EF∥OD
即∠BDO就是直线BD与EF所成的角 …………9分
![]()
直线BD与EF所成的角为![]() …………12分
…………12分
20.解: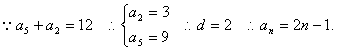 …………3分
…………3分
![]() …………4分
…………4分

![]() …………7分
…………7分
(2)![]()
![]()
![]() …………12分
…………12分
21.解:(1)∵直线与椭圆相交,联立方程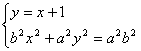
![]() …………2分
…………2分
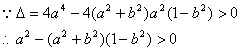
![]() …………5分
…………5分
(2)![]() …………6分
…………6分
设交点![]()
由(1)知:![]()
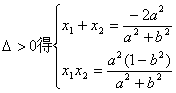 …………9分
…………9分
以AB为直径的圆过原点,则OA⊥OB,从而![]()
即![]() …………10分
…………10分
把韦达定理式代入
![]()
因![]() …………12分
…………12分
22.解:(1)函数定义域为(—1,+∞) …………1分
![]() …………2分
…………2分
由![]()
∴增区间:![]() ,减区间:(—1,0) …………4分
,减区间:(—1,0) …………4分
(2)由![]() ,列表:
,列表:
![]()
![]() —
+
—
+
![]() ↓
↑ …………6分
↓
↑ …………6分
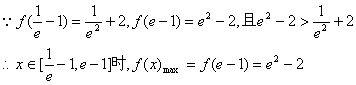
![]() 恒成立。 …………8分
恒成立。 …………8分
(3)![]() …………9分
…………9分

…………12分