08届高中毕业生理科数学二月调研测试试题

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填在试题卷和答题卡上，并将准考号条形码粘贴在答题卡上的指定位置。

2．选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。非选择题用黑色墨水的签字笔或钢笔直接答在答题卡。答在试题卷上无效。

3．考试结束，监考人员将本试题卷和答题卡一并收回。

参考公式：

如果事件互斥，那么

如果事件相互独立，那么

如果事件在一次试验中发生的概率是，那么次独立重复试验中事件恰好发生次的概率　　

球的表面积公式　　其中R表示球的半径

球的体积公式　　其中R表示球的半径

一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的

1．　复数满足方程：，则=

A、　 　　　　　　　　　B、　　 　　　　　　　C、　 　　　　　 D、

2．　在等差数列中，=9，=3，则=

A、0　 　　　　　　　　　　　 B、3　 　　　　　　　　　　　 C、6　 　　　　　　　　　　D、-3

3．　二项式的展开式中含有非零常数项，则正整数的最小值为

A、7　 　　　　　　　　　 B、12　 　　　　　　　　　　　 C、14　 　　　　　　　　　　 D、5

4．　函数的单调递增区间为

A、　　　　　　 　 B、　　　　　　　　C、_D、

_{5．下面给出四个命题：}

①　　　 直线与平面内两直线都垂直，则。②经过直线有且仅有一个平面垂直于直线 ③过平面外两点，有且只有一个平面与垂直。④直线同时垂直于平面、，则∥。其中正确的命题个数为

A、0　　 　　　　　　　　　 B、1　　　　　　　　　　　　 C、2　　　　　　　　　　　　 D、3

6．某一批袋装大米质量服从正态分布N（10，0.01）（单位：kg），任选一袋大米，它的质量在9.8kg-10.2kg内的概率是

A、1-(2)　　　　 B、2(2)-1　　 　　　　　C、F(2)-F(-2)　　　　　 D、F(2)+F(-2)-1

7.在(0,)内，使成立的的取值范围为

A、[]　　　　　　 B、[]　 　　　　　　 C、[]　　　　　 D、[]

8．已知平面内的四边形ABCD和该平面内任一点P满足：，那么四边形ABCD一定是

A、梯形　　  　　　　　　B、菱形　　　　　　　　　　C、矩形　　 　　　　　　　D、正方形

9．在四面体ABCD中，三组对棱棱长分别相等且依次为，5则此四面体ABCD的外接球的半径R为

A、　 　　　　　　　　B、5　　　　　　　　　　　　　C、　　　　　　　　　　　　 D、4

10．过原点O作两条相互垂直的直线分别与椭圆P：交于A、C与B、D，则四边形ABCD面积最小值为

A、　　　　　　　　　　　 B、　　　　　　　　　　C、　　　　　　　　　　　　 D、

二．填空题：本大题共5小题，每小题5分，共25分，把答案填在题在横线上。

11．已知变量,满足约束条件，则的最大值为　　　　  　 。

12．常数满足 则=　　　　　　 .

13．从4双不同鞋子中取出4只鞋，其中至少有2只鞋配成一双的取法种数为　　　　　 .

（将计算的结果用数字作答）

14．已知圆C：，一动直线l过A (-1，O)与圆C相交于P、Q两点，M为PQ中点，l与直线相交于N，则　　　　　　 。

15．当时，恒成立，则实数的取值范围为　　　　　  。

三．解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤。

16．（本小题满分12分）

如图，在△ABC中，角A、B、C的对边分别为、、c,且8=7，c=，AB边上的高CM长为。　　　　　　　　　　　　　　　　　　 

（1）　　　 求的值

（2）　　　 求△ABC的面积

17．（本小题满分12分）

如图，在棱长为l的正方体ABCD-A₁B₁C₁D₁中，M为CC₁中点。

（1）　　　 求二面角A₁ –BD -M的大小；

（2）　　　 求四面体A₁ -BDM的体积；

18．（本小题满分12分）

有10张形状、大小相同的卡片，其中2张上写着数字O，另外5张上写着数字1，余下3张上写着数字2。从中随机地取出1张，记下它的数字后放回原处。当这种手续重复进行2次时，为所记下的两个数之和。

(1)求=2时的概率；

(2)求的数学期望；

19．（本小题满分12分）

过双曲线C：的右顶点A作两条斜率分别为k₁、k₂的直线AM、AN交双曲线C于M、N两点，其k₁、k₂满足关系式且，

(1)求直线MN的斜率；

(2)当m²=时，若，求直线MA、NA的方程；

20．（本小题满分13分）

在数列中，，其中且，且满足关系式：

(1)猜想出数列的通项公式并用数学归纳法证明之；

(2)求证：，.

21．（本小题满分14分）

（1）求证：当时，不等式对于恒成立 .

（2）对于在（0,1）中的任一个常数，问是否存在使得成立？

如果存在，求出符合条件的一个；否则说明理由。

08届高中毕业生理科数学二月调研测试试题参考答案及评分细则

一．选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	C	A	A	D	B	B	D	C	C	A

二．填空题

11、3　　　12、3　　 13、54　　　14、5　　 15、[]

三．解答题

16．解：（1）∵，故设=7k，b=8k（k>0），由余弦定理可=（7²+8² -2×7×8cos120⁰）k²=169k²，∴c=13k，因此……（6分）

（2）∵，∴

∴…………………（12分）

17．解：（1）在正方体ABCD—A₁B₁C₁D₁中，棱长为l，取BD中点为O，连结OM，OA_1。

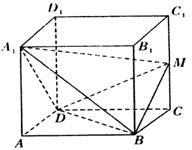∵BM=DM=，A₁B=A₁D=

从而

∴为=两角A₁—BD—M的平面角

在中，

而

从而由勾股定理可知：…………………………………………（6分）

（2）由(1)可知面BDM，从而四面体-BDM体积

…………………………………（12分）

18．解：（1）卡片的出法有(0,0),(0,1),(1,0),(0,2),(2,0),(1,1),(1,2),(2,1),(2,2)共9种

而=2时，出现三种(0,2),(2,0),(1,1)

故……（6分）

（2）同(1)处理方法可求　，，

，

因此，的数学期望……（12分）

19.解：(1)C：的右顶点A坐标为(1,0)

设MA直线方程为，代入中，则，整理得

由韦达定理可知，而，又

∴

于是

同理可知，∴有，∴MN∥抽，从而MN直线率…（6分）

（2）∵，∴AM到AN的角为或AN到AM的角为。

则或，又，

从而

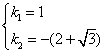则求得 或

因此MA，NA的直线的方程为,

或为，……（12分）

20．（1）解：由原递推式得到

　

猜想得到……（3分）

下面用数学归纳法证明

1⁰当n=1时　 a₁=t—1　 满足条件

2⁰假设当n=k时，

则

∴

∴

即当n=k+1时，原命题也成立。

由1⁰、2⁰知……（7分）

(2)

而

故t>0，且时有，即……（13分）

21．（1）证明：(Ⅰ)在时，要使成立。

只需证：即需证：　　　 ①

令，求导数

∴，又，求，故

∴为增函数，故，从而①式得证

（Ⅱ）在时，要使成立。

只需证：，即需证：　　　　 ②

令，求导数得

而在时为增函数

故，从而

∴在时为减函数，则，从而②式得证

由于①②讨论可知，原不等式在时，恒成立……（6分）

（2）解：将变形为　　　 ③

要找一个X₀>0，使③式成立，只需找到函数的最小值，

满足即可，对求导数

令得，则x= -lna，取X₀= -lna

在0< x < -lna时，，在x > -lna时，

在x=-lna时，取得最小值

下面只需证明：，在时成立即可

又令，对关于求导数

则，从而为增函数

则，从而得证

于是的最小值

因此可找到一个常数，使得③式成立　 ……（14分）