高考数学试题精选(五)
卞志业 2008-1-17
1.(0801哈尔滨)设复数![]() ,若
,若![]() 为实数,则
为实数,则![]() 等于 ( )
等于 ( )
A.-2 B.-1 C. 1 D.2
2. (0712河北唐山)双曲线![]() 的两个焦点为
的两个焦点为![]() ,
,![]() 在双曲线上,且满足
在双曲线上,且满足![]() 则
则![]() 的面积为 ( )
的面积为 ( )
A.![]() B.1 C.2 D.4
B.1 C.2 D.4
3. (0801湖南长郡)已知![]() ,0是原点,点
,0是原点,点![]() 的坐标满足
的坐标满足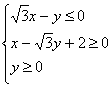 则
则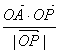 的取值范围是( )
的取值范围是( )
A、(0,3) B、[0,3] C、(-3,3) D、[-3,3]
4. (0801湖南长郡)已知对任意实数x,使![]() 且
且![]() 时,
时,![]() ,则
,则![]() 时,有( )
时,有( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5.(0801哈尔滨)已知O为直角坐标系原点,P、Q坐标均满足不等式组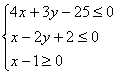 则
则![]() 取最小值时的
取最小值时的![]() 的大小为 ( )
的大小为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(理科)(0801哈尔滨)![]() 的概率密度函数
的概率密度函数![]() ,则下列错误的选项是 ( )
,则下列错误的选项是 ( )
A.![]() B.
B.![]()
C.![]() 的渐近线为
的渐近线为![]() D.
D. ![]() ~
~![]()
6.(0705山东聊城)已知点P(-3,1)在椭圆![]() 的左准线上,过点P且方向向量为a(2,-5)的入射光线,经直线y=-2反射后过椭圆的左焦点,则椭圆的离心率为( )
的左准线上,过点P且方向向量为a(2,-5)的入射光线,经直线y=-2反射后过椭圆的左焦点,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(0801河南郑州)以正方体的顶点为顶点的三棱锥的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(0712河北唐山)![]() 的
的![]() 边上的高为
边上的高为![]() ,
,![]() ,
,![]() 且
且![]() 将
将![]() 沿
沿![]() 折成大小为
折成大小为![]() 的二面角
的二面角![]() ,若
,若![]() ,则三棱锥
,则三棱锥![]() 的侧面
的侧面![]() 是(
)
是(
)
A.锐角三角形 B.钝角三角形
C.直角三角形 D.形状与![]() 的值有关的三角形
的值有关的三角形
9.(0712河北唐山)设![]() 分别为具有公共焦点F1与F2的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足
分别为具有公共焦点F1与F2的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足![]() ,则
,则![]() 的值为(
)
的值为(
)
A.1 B.![]() C.2 D.不确定
C.2 D.不确定
10.(0801湖南师大附中)已知数列{an}的通项公式![]() ,设前n项和为Sn,则使Sn<-5成立的自然数n ( )
,设前n项和为Sn,则使Sn<-5成立的自然数n ( )
A.有最大值63 B.有最小值63 C.有最大值31 D.有最小值31
11.(0801哈尔滨)在圆![]() 内过点
内过点![]() 有
有![]() 条长度成等差数列的弦,其中最短弦长为数列的首项
条长度成等差数列的弦,其中最短弦长为数列的首项![]() ,最长弦长为
,最长弦长为![]() ,若公差
,若公差![]() ,那么
,那么![]() 取值的集合为 ( )
取值的集合为 ( )
A.{4,5,6} B.{6,7,8,9} C.{3,4,5} D.{3,4,5,6}
12.(0801哈尔滨)已知M是椭圆![]() 上的点,两焦点为
上的点,两焦点为![]() ,点
,点![]() 是
是![]() 的内心,连结
的内心,连结![]() 并延长交线段
并延长交线段![]() 于
于![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.(0712山东邹平)已知双曲线![]() 的离心率
的离心率![]() ,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为
,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为![]() ,则
,则![]() 的取值范围是
.
的取值范围是
.
14.(0712山东邹平)如图,空间有两个正方形ABCD和ADEF,M、N分
别为BD、AE的中点,则下列结论中正确的是
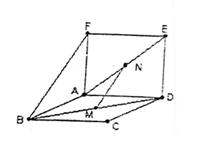 (填写所有正确结论对应的序号)
(填写所有正确结论对应的序号)
①MN⊥AD;
②MN与BF的是对异面直线;
③MN//平面ABF
④MN与AB的所成角为60°
15. (0801哈尔滨)动点P为椭圆![]() 上异于椭圆顶点
上异于椭圆顶点![]() 的一点,F1,F2为椭圆的两个焦点,动圆C与线段F1P,F1F2的延长线及线段PF2相切,则圆心C的轨迹是____________________
的一点,F1,F2为椭圆的两个焦点,动圆C与线段F1P,F1F2的延长线及线段PF2相切,则圆心C的轨迹是____________________
16.(0712浙江五校)有三颗骰子A、B、C,A的表面分别刻有1,2,3,4,5,6,B的表面分别刻有1,3,5,7,9,11,C的表面分别刻有2,4,6,8,10,12,则抛掷三颗骰子后向上的点数之和为12的概率是
17. (0712河北唐山)已知函数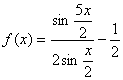 . (1)将
. (1)将![]() 化成
化成![]() 的整式;
的整式;
(2)若![]() 与
与![]() 的图像在
的图像在![]() 内至少有一个公共点,试求
内至少有一个公共点,试求![]() 的范围。
的范围。
18.(理科)(0801哈尔滨)某商场进行促销活动,促销方案为顾客消费1000元可获得奖券一张,每张奖券中奖的概率为![]() ,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得到2张奖券,于是小李补偿50元给同事购买了一台价格600元的小灵通,这样小李可以得到3张奖券,小李抽奖后实际支出为
,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得到2张奖券,于是小李补偿50元给同事购买了一台价格600元的小灵通,这样小李可以得到3张奖券,小李抽奖后实际支出为![]() (元)。
(元)。
(1)求![]() 的分布列;
的分布列;
(2)说明小李出资50元增加一张奖券是否划算。
18.(0801哈尔滨)一袋中装有分别标记着1、2、3、4、5数字的5个球
(1)从袋中一次取出3个球,试求3个球中最大数字为4的概率;
(2)从袋中每次取出1个球,取出后放回,连续取三次,试求取出的3个球中最大数字
为4的概率。
19.(0712河北唐山)如图所示,正三棱柱![]() 的底面边长为a,点M在BC上,
的底面边长为a,点M在BC上,![]() 是以点M为直角顶点的等腰直角三角形。
是以点M为直角顶点的等腰直角三角形。
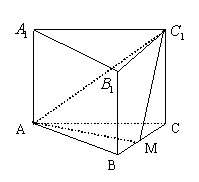 (Ⅰ)求证:点M为边BC的中点;
(Ⅰ)求证:点M为边BC的中点;
(Ⅱ)求点C到平面![]() 的距离;
的距离;
(Ⅲ)求二面角![]() 的大小。
的大小。
20.(0801江苏如东)已知二次函数![]() 满足:对任意实数x,都有
满足:对任意实数x,都有![]() ,且当
,且当![]() (1,3)时,有
(1,3)时,有![]() 成立。
成立。
(1)证明:![]() 。
(2)若
。
(2)若![]() 的表达式。
的表达式。
(3)设![]()
![]() ,若
,若![]() 图上的点都位于直线
图上的点都位于直线![]() 的上方,求实数m的取值范围。
的上方,求实数m的取值范围。
21.(0712河北唐山)设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 是抛物线上的两点
是抛物线上的两点![]() ,且
,且![]() 与
与![]() 为共线向量。(1) 求
为共线向量。(1) 求![]() 的值;(2)
的值;(2)![]() 上是否存在点
上是否存在点![]() 使
使![]() ,证明你的结论。
,证明你的结论。
22.(理科)(0712浙江五校)已知二次函数![]() 有最大值且最大值为正实数,集合
有最大值且最大值为正实数,集合![]() ,集合
,集合![]()
(1)求![]() 和
和![]() ;
;
(2)定义![]() 与
与![]() 的差集:
的差集:![]() 且
且![]() ,设
,设![]() ,
,![]() ,x均为整数,且
,x均为整数,且![]() ,
,![]() 为
为![]() 取自A-B的概率,
取自A-B的概率,![]() 为x取自A∩B的概率,写出
为x取自A∩B的概率,写出![]() 与b的三组值,使
与b的三组值,使![]() ,
,![]() ,并分别写出所有满足上述条件的
,并分别写出所有满足上述条件的![]() (从大到小)、b(从小到大)依次构成的数列{
(从大到小)、b(从小到大)依次构成的数列{![]() }、{bn}的通项公式(不必证明);
}、{bn}的通项公式(不必证明);
(3)若函数![]() 中,
中,![]() ,
,![]() ,设t1、t2是方程
,设t1、t2是方程![]() 的两个根,判断
的两个根,判断![]() 是否存在最大值及最小值,若存在,求出相应的值;若不存在,请说明理由
是否存在最大值及最小值,若存在,求出相应的值;若不存在,请说明理由
22.(0712浙江五校)已知数列![]() 中
中![]() ,数列{bn}满足:
,数列{bn}满足:![]()
(1)求证:数列{bn}是等差数列;
(2)求数列{an}中的最大项与最小项,并说明理由;
(3)设![]() .
.
答案
一、选择题:本大题主要考查基本知识和基本运算 共12小题,每小题5分,满分60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | B | B | D | B | D | C
| D | C | C | B | A | C |
二、填空题: 本大题主要考查基本知识和基本运算. 本大题共4小题,每小题4分,满分16分。
13. ![]() 14. 1,3 _
14. 1,3 _
15. 直线,其方程为:x=a且y≠0 16. ![]()
三、解答题: 本大题共6小题,其中17~21题每题12分,22题14分,满分74分.解答应写出文字说明、演算步骤或推证过程.
17.(1)![]() (2)
(2)![]()
18.(1)ξ可能取值为-550,450,1450,2450。
![]()
![]()
ξ的分布列为:
| P | -550 | 450 | 1450 | 2450 |
| ξ |
|
|
|
|
(2)小李出资50元,抽奖后实际支出为ξ
则 ![]()
小李不出资50元,抽资后实际支出为η
则η可取400,1400,2400
![]()
![]()
则 Eη=![]()
Eη>Eξ说明小李出资50元增加一张奖券划算。
18.解:①从袋中一次取3个球,其中最大数字为4的概率为P,则![]()
②含一个数字4的概率为![]()
含二个数字4的概率为![]()
含三个数字4的概率为![]()
故含最大数字为4的概率为![]()
19. (Ⅰ)证明 ![]()
![]() 是以点M为直角顶点的等腰直角三角形,
是以点M为直角顶点的等腰直角三角形,
∴![]() 且
且![]()
![]() 正三棱柱
正三棱柱![]()
∴![]() 底面ABC
底面ABC
∴![]() 在底面内的射影为CM,
在底面内的射影为CM,![]()
![]() 底面ABC为边长为a的正三角形,
底面ABC为边长为a的正三角形,
∴点M为BC边的中点。
(Ⅱ)解:过点C作![]() ,
,
由(Ⅰ)知![]() 且
且![]()
∴![]()
![]() CH在平面
CH在平面![]() 内,
内,
∴![]() ,
,
∴![]() ,
,
由(Ⅰ)知![]()
∴![]()
∴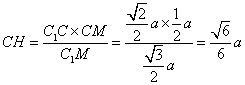
∴点C到平面![]() 的距离为
的距离为![]()
(Ⅲ)解:过点C作![]() 于I,连HI,
于I,连HI,![]()
![]()
∴HI为CI在平面![]() 内的射影
内的射影
∴![]() ,
,![]() 是二面角
是二面角![]() 的平面角
的平面角
![]() 在直角三角形
在直角三角形![]() 中,
中,
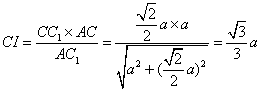
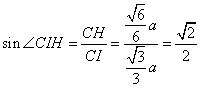
∴![]()
∴二面角![]() 的大小为
的大小为![]()
20. 解:(1)由条件知 ![]() 恒成立
恒成立
又∵取x=2时,![]() 与恒成立
与恒成立
∴![]() …………4分
…………4分
(2)∵![]() ∴
∴![]() ∴
∴![]() ……6分
……6分
又 ![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
∴![]() , …………10分
, …………10分
解出:![]() ,∴
,∴![]() …………12分
…………12分
(3)由分析条件知道,只要![]() 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 ![]() 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率![]() 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
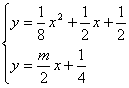 利用相切时△=0,解出
利用相切时△=0,解出 ![]()
∴![]() …………16分
…………16分
解法2:![]() 必须恒成立
必须恒成立
即 ![]() 恒成立
恒成立
①△<0,即 [4(1-m)]2-8<0,解得:![]()
②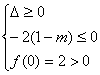 解出:
解出:![]()
总之,![]() ………16分
………16分
21.(1)![]() (2)存在点
(2)存在点![]() 使结论成立。
使结论成立。
22.(1)∵函数![]() 有最大值, ∴
有最大值, ∴![]()
由于![]() ,而最大值为正数,则
,而最大值为正数,则![]() ,∴
,∴![]()
∴![]() ,
,![]() ……………………3分
……………………3分
(2)要使![]() ,
,![]() ,可以使
,可以使
①![]() 中有3个元素,
中有3个元素,![]() 中有2个元素,
中有2个元素, ![]() 中有1个元素,
中有1个元素,
则![]() ,
,![]()
②![]() 中有6个元素,
中有6个元素,![]() 中有4个元素,
中有4个元素, ![]() 中有2个元素
中有2个元素
则![]() ,
,![]()
③![]() 中有9个元素,
中有9个元素,![]() 中有6个元素,
中有6个元素,![]() 中有3个元素
中有3个元素
则![]() ,
,![]()
因此,![]() ,
,![]() …………………………………6分
…………………………………6分
(3)对于方程![]() ,
,![]() ,
,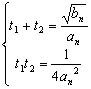
![]()
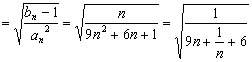
![]() 在N上单调递减
在N上单调递减
∴ ![]() ,不存在最小值…………………6分
,不存在最小值…………………6分
22. (1)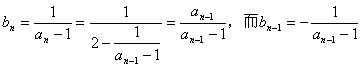
∴![]()
∴{bn}是首项为![]() ,公差为1的等差数列 …………4分
,公差为1的等差数列 …………4分
(2)依题意有![]()
∴![]()
函数![]() 上为减函数. 在(-
上为减函数. 在(-![]() ,3.5)上也为减函数.
,3.5)上也为减函数.
故当n=4时,![]() 取最大值3,n=3时,取最小值-1 …………5分
取最大值3,n=3时,取最小值-1 …………5分
(3)∵![]()
∴![]() ,
,
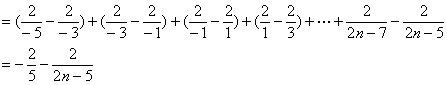
∴当n=2时,Sn取最大值![]() ,当n=3时,Sn取最小值
,当n=3时,Sn取最小值![]()
∴![]() ……………………5分
……………………5分