专题考案(2)数列板块 第4课 数列的应用

(时间：90分钟　满分：100分)

题型示例

某厂试制新产品，为生产此项产品需增加某些设备，购置这些设备需一次付款25万元，若租用这些设备每年初需付租金3.3万元，若一年期存款的年利率为9.8％，试讨论哪种方案的收益更大(设备寿命为10年).

解　从10年后的价值考虑，购置设备的25万元，10年后的价值为：M₁=25(1+9.8％)¹⁰≈63.674(万元)，每年初付租金3.3万元的10年后的总价值为：

M₂=3.3×(1+9.8％)¹⁰+3.3×(1+9.8％)⁹+…+3.3×(1+9.8％)=3.3×1.098×≈57.197(万元).

即租用设备方案的收益更大.

点评　优化方案的问题，即为获得利润最大的方式.

一、选择题(8×3′＝24′)

1．农民收入由工资性收入和其他收入两部分构成.2003年某地区农民人均收入3 150元(其中工资性收入为1800元，其他收入为1350元)，预计该地区自2004年起的5年内，农民的工资性收入将以每年6%的年增长率增长，其他收入每年增加160元，根据以上数据，2008年该地区农民人均收入介于　　　　　　　　　　　　　　　　　　　　　 (　　)

A.4200元~4400元　　　　  B.4400元~4600元

C.4600元~4800元　　　　  D.4800元~5000元

2．已知数列1，1，2，…它的每一项由一个等比数列和一个首项为0的等差数列对应项相加而得，那么这个数列的前10项和为　　　　　　　　　　　　　　　　　　  (　　)

A.467　　　　B.557　　　　C.978　　　　D.1068

3．凸多边形各内角度数成等差数列，最小角为120°，公差为5°，则边数n等于 (　　)

A.16　　　　 B.9　　　　C.16或9　　　　D.12

4．首项是2，公比是3的等比数列，从第n项到第N项的和为720，则n,N的值分别是(　　)

A.n=2,N=6　　　B.n=2,N>6　　　C.n=3,N=6　　　D.n=3,N>6

5．已知等差数列｛a_n｝的各项均为正数，公差d≠0，设P=，则P与Q的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.P>Q　　　　B.P<Q　　　　C.P=Q　　　　D.无法确定

6．一个机器猫每秒前进或后退一步，程序设计人员让机器猫以每前进3步，然后再后退2步的规律移动；如果将此机器猫放在数轴的原点上，面向正的方向，以1步的距离为1个单位长，令P(n)表示第n　s时机器猫所在的位置的坐标，且P(0)=0,那么下列结论中错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.P(3)=3　　　B.P(5)=1　　　C.P(101)=21　　　D.P(103)<P(104)

7．已知｛a_n｝是首项为50，公差为2的等差数列，｛b_n｝是首项为10，公差为4的等差数列.设以a_k，b_k为相邻两边的矩形内最大圆的面积为S_k，若k≤21，那么S_k等于　 (　　)

A.π(2k+1)²　　 B.π(k+12)² 　　 C.π(2k+3)²　　 D.π(k+24)²

8．一个正数组成的等比数列前7项之和是2，其后14项之和是12，则再后面21项之和

是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.110　　　　B.108　　　　C.104　　　　D.112

二、填空题(4×4′＝16′)

9．若A、B、C成等差数列，则直线Ax+By+C=0，必过点　　　　　 .

10．已知f(x)为一次函数，若f(3)=15,且f(2)、f(5)、f(14)成等比数列，则f(1)+f(2)+…

+f(n)=　　　　　 .

11．大楼共n层(n为奇数)，现每层指定一人，共n人集中到第k层开会，要使n位参会

人员上、下楼梯所走路程总和最短(假定相邻两层楼梯长相等，为a)，则k=　　　　　 .

12．有一堆物品，某层放n²个，而它的上一层比它少放(2n-1)个(n≥2),已知这堆物品底层放100个，顶层放16个，这堆物品共有　　　　个.

三、解答题(3×12′＝36′)

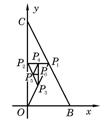13．如图，△OBC的三个顶点坐标分别为(0,0)、(1，0)、(0，2)，

设P₁为线段BC的中点，P₂为线段CO的中点，P₃为线段OP₁的

中点，对于每一个正整数n,P_n+3为线段P_nP_n+1的中点，令P_n的坐

标为(x_n,y_n)，a_n=y_n+y_n+1+y_n+2.

图1

(1)求a₁,a₂,a₃及a_n;

(2)证明y_n+4=1-,n∈N*;

(3)若记b_n=y_4n+4-y_4n,n∈N*,证明{b_n}是等比数列.

14．某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不进行技术改造，预测从今年起每年比上一年纯利润减少20万元.今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年(今

年为第一年)的利润为500（1+）万元(n为正整数).

(1)设从今年起的前n年，若该企业不进行技术改造的累计纯利润为A_n万元，进行技术改造后的累计纯利润为B_n万元(须扣除技术改造资金)，求A_n,B_n的表达式;

(2)依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？

15．△ABC中，内角A、B、C成等比数列，且b²-a²=ac，求A、B、C.

四、思考与讨论(2×12′＝24′)

16．设a>0，a≠1，f(x)=log_a(x+)(x≥1)．

(1)求f(x)的反函数f^-1(x)及其定义域；

(2)设b_n=f^-1(n),S_n=b₁+b₂+…+b_n,试求证当log₂a<1时，对于n∈N*，有S_n＜2ⁿ-()ⁿ.

17．试判断，能否构造一个实数等比数列{a_n},使其满足下列三个条件:①a₁+a₆=11;②a₃·a₄=;③至少存在一个自然数m,使a_m-1,a,a_m+1+依次成等差数列.若能，请写出这个数列的通项公式；若不能，请说明理由.

参考答案

1．B　设从2003年起第n年的收入为y,则有y=1800(1+6%)^n-1+［1350+(n-1)·160］

2003年为当n=1时，则2008年为n=6,故2008年农民收入1800（1+6%）⁵+（1350+5×160）∈(4400,4600).

2．C　等差数列:a₁=0，d=-1，∴S₁₀=-45，等比数列:b₁=1，q=2,∴S′₁₀=1023.

3．B　凸多边形内角和为(n-2)·180°，最大内角小于180°.

4．C　S^N-S_n-1=3^N-3^n-1=720，再用代入法验证.

5．A　∵d≠0,∴a₅≠a₇，∴

6．D　先列出数列P(n)的前n项，即0,1,2,3,2,1,2,3,4,…可推得P(5n)=n,

P(5n+1)=n+1,P(5n+2)=n+2,P(5n+3)=n+3,P(5n+4)=n+2(n∈N),

∴P(3)=3,P(5)=1,P(101)=P(20×5+1)=20+1=21.所以A、B、C均正确.

P(103)=P(20×5+3)=23,P(104)=P(20×5+4)=20+2=22,则P(103)>P(104).故选D.

7．C　a_k=2k+48,b_k=4k+6，∵k≤21,∴b_k≤a_k，故以b_k为直径.

8．D　每7项之和构成的数列记为｛A_n｝，则｛Ａ_n｝是等比数列，设公比为q,

q=2A₄＋Ａ₅＋Ａ₆=112.

9．(1，-2)　∵2B=A+C，∴A-2B+C=0，∴必过点(1,-2).

10．3n²　设f(x)=ax+b,则f(x)=6x-3,再求和.

11．路程总和s=a［1+2+…+(k-1)］+0+a·［1+2+…+(n-k)］=［k²-(n+1)k+］·a.

∵a>0,且n为奇数，∴k=时s最小.

12．371　若某层放n²个,则它的上一层放n²-(2n-1)=(n-1)²个,设此堆物品共m层，则

(10-m+1)²=16,所以m=7,故此堆物品共7层.共有物品10²+9²+…+4²=-

(1²+2²+3²)=371个.

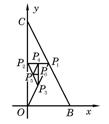13．分析　（1）由赋值法求a₁,a₂,a₃,由中点坐标公式得到y_n,y_n+1,y_n+3关系，再求得a_n+1=a_n，从而{a_n}为常数列.

(2)由上式，再结合中点坐标公式，原式即得证.

(3)由（2）式即可得到b_n+1=-b_n关系，原式即得证.

(1)解　因为y₁=y₂=y₄=1,y₃=,y₅=,所以a₁=a₂=a₃=2.

图2

又由题意可知y_n+3=.

∴a_n+1=y_n+1+y_n+2+y_n+3=y_n+1+y_n+2+=y_n+y_n+1+y_n+2=a_n,∴{a_n}为常数列.

∴a_n=a₁=2,n∈N*.

(2)证明　将等式y_n+y_n+1+y_n+2=2两边除以2，得y_n+=1,

又∵y_n+4=,∴y_n+4=1-，n∈N*.

(3)∵b_n+1=y_4n+8-y_4n+4==- (y_4n+4-y_4n)= -b_n,

又∵b₁=y₈-y₄=-≠0,∴{b_n}是公比为-的等比数列.

点评　本题通过一类几何图形的坐标作为切入点，既考查了学生的几何知识又考查了代数知识，但侧重于数列递推关系式的应用，又涉及等比数列一系列知识.能力方面考查学生对所给条件的灵活运用，及综合运用能力，解决问题的创新能力.

14．分析　A_n,B_n由题意很容易即可求出，通过作差法比较B_n与A_n的大小，B_n-A_n是关于n的函数关系式，本题即可求解.

解　（1）依题设，A_n=（500-20）+（500-40）+…+（500-20n）=490n-10n²

B_n=500-600=500n--100.

(2)B_n-A_n=-(490n-10n²)=10n²+10n--100=10

因为函数y=n(n+1)--10在（0,+∞）上为增函数，

当1≤n≤3时，n(n+1)--10≤12--10<0;

当n≥4时，n(n+1)--10≥20--10>0.

∴仅当n≥4时，B_n>A_n.

答:至少经过4年，该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.

点评　本题通过一个具体的经济问题，来考查学生建立函数关系式、数列求和，以及不等式基础知识，考查运用数学知识解决实际问题的能力.

15．解　由余弦定理:b²=a²＋c²-2ac·cosB，∴b²-a²=c²-2ac·cosB，

∴ac=c²-2ac·cosB，∴c²=ac(1+2cosB).

再由正弦定理得

sinC=sinA(1+2cosB)=sinA+2sinAcosB=sinA+sinC+sin(A-B)，∴sinA+sin(A-B)=0.

∴2sin(A-)cos=0，显然cos≠0，∴sin(A-)=0,∴A=.

即B=2A,又A、B、C成等比数列，∴C=4A.

∴A+2A+4A=π.∴A=，B=，C=.

16．解　(1)由y=log_a(x+)(x≥1)，得x=(a^y+a^-y)∴f^-1(x)= (a^x+a^-x)．

当a>1时，f^-1(x)的定义域为［0,+∞］；

当0<a<1时，f^-1(x)的定义域为(-∞，0)．

(2)依题意，得b_n=(aⁿ+a^-n)(n∈N*)

∴S_n=(a+a^-1)+(a²+a^-2)+…+(aⁿ+a^-n)=(a+a²+…+aⁿ)+(a^-1+a^-2+…+a^-n)

=

∵log₂a<1，∴-1<log₂a<1,又n∈N*，∴a>1.因而1<a<2.

由于a+,a²+，…，aⁿ+在(1，2)递增．

∴S_n<(2+2²+…+2ⁿ)+(+)=2ⁿ-1+(1-)=2ⁿ--．

∵+>2=()ⁿ，∴2ⁿ--<2ⁿ-()ⁿ．因此S_n<2ⁿ-()ⁿ．

17．解　设数列{a_n}的公比为q,∵a₁a₆=a₃a₄,∴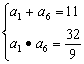

解得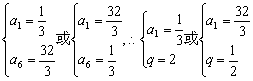

∴满足条件①②的数列的通项公式必为:

a_n=·2^n-1或a_n=·2^6-n

对于a_n=·2^n-1,若存在题设要求的m,则2(·2^m-1)²=··2^m-2+·2^m+

∴2^2m-7·2^m-8=0,∴(2^m+1)(2^m-8)=0，∴2^m=8即m=3.

对于a_n=·2^6-n,若存在题设要求的m,则同理有:4·(2^6-m)²-11·2^6-m-8=0

令t=2^6-m,则有4t²-11t-8=0

由于Δ=11²+16×8=249,不是完全平方数.∴符合条件的m不存在.

综上知，能构造出这样的等比数列，其通项公式为a_n=·2^n-1.