专题十一 三角形中的边角关系
1.
在![]() 中,
中,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
2.
在![]() 中,已知
中,已知![]() ,那么
,那么![]() 一定是(
)
一定是(
)
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等边三角形
3.
在![]() 中,若
中,若![]() ,则
,则![]() 的值为__________.
的值为__________.
4.
已知![]() 、
、![]() 、
、![]() 是
是![]() 的三个内角,
的三个内角,![]() ,
,![]() 是方程
是方程![]() 的两个实根,则
的两个实根,则![]() _____________,
_____________,![]() _____________.
_____________.
5.
已知![]() 、
、![]() 、
、![]() 是
是![]() 的三个内角,若
的三个内角,若![]() 和
和![]() 分别是关于
分别是关于![]() 的方程
的方程![]() 的两个实根,则角
的两个实根,则角![]() _______________;实数
_______________;实数![]() 的取值范围是__________________.
的取值范围是__________________.
6.
在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
⑴ 求![]() 的值;
的值;
⑵ 若![]() ,
,![]() 的面积
的面积![]() ,求
,求![]() .
.
7.
在![]() 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
⑴ 求角B的大小;
⑵ 若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
8.
在![]() 中,角A、B、C所对的边的长分别为a、b、c,且
中,角A、B、C所对的边的长分别为a、b、c,且![]() ,若向量
,若向量![]() ,
,![]() ,且
,且![]() .
.
⑴ 求A的大小; ⑵ 求![]() 的值.
的值.
9.
在![]() 中,
中,![]() 、
、![]() 、
、![]() 为角A、B、C的对边,且
为角A、B、C的对边,且![]()
![]() .
.
⑴ 求![]() 的值; ⑵ 若
的值; ⑵ 若![]() ,求
,求![]() 的最大值.
的最大值.
10.
在![]() 中,角A、B、C的对边为
中,角A、B、C的对边为![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
⑴ 求角![]() 的大小;
的大小;
⑵ 设向量![]() ,
,![]()
![]() ,且
,且![]() 的最大值为5,求实数
的最大值为5,求实数![]() 的值.
的值.
11.
在![]() 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() .
.
⑴ 求![]() 的值;
的值;
⑵ 若![]() 最长的边为1,求最短边的长.
最长的边为1,求最短边的长.
12.
在![]() 中,
中,![]() 、
、![]() 、
、![]() 为三个内角,
为三个内角,![]() .
.
⑴ 若![]() ,求角
,求角![]() ;
;
⑵ 若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
答案:
1.C 2.B
3.![]() 4.
4.![]() ,
,![]() 5.
5.![]() ;
;![]()
6.解:⑴![]() =
=![]() =
=![]()
⑵∵![]() 分
分
由![]()
由余弦定理a2=b2+c2-2bccosA可得:
![]()
![]() .
.
7.⑴ 解法一:由正弦定理![]() 得
得
![]()
将上式代入已知![]()
即![]()
![]()
∵A+B+C=![]() ,
,![]()
![]() 为三角形的内角,
为三角形的内角,![]() .
.
解法二:由余弦定理得![]() ,
,
将上式代入![]()
整理得![]()
![]() 为三角形的内角,
为三角形的内角,![]() .
.
⑵ 将![]() 代入余弦定理
代入余弦定理![]() 得
得
![]()
![]()
8.解:(1)由m//n得![]()
即![]()
![]()
![]() 舍去
舍去 ![]()
(2)![]()
由正弦定理,![]()
![]()
![]()
![]()
9.解:(1)由已知得![]()
![]() ,
,
![]()
又![]()
(2)由余弦定理,得![]()
即![]()
![]()
当且仅当![]() 时取等号. 所以ac的最大值为9.
时取等号. 所以ac的最大值为9.
10.解:(I)因为![]()
所以![]()
整理得![]()
所以![]() ,
,
因为![]()
(2)![]()
![]()
设![]()
所以,当![]() 取得最大值.
取得最大值.
依题意![]() ,符合题意.所以,
,符合题意.所以,![]() .
.
11.解:(I)因为![]() 所以B为锐角,
所以B为锐角,
所以![]() 所以
所以![]() ,
,
又![]()
所以tanC=-1.
(Ⅱ)由![]()
所以c边最大,即c=1.
又因为![]() 边最小.
边最小.
因为![]() 所以,
所以,
12.解:(Ⅰ)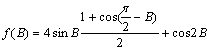
=![]()
![]()
因为![]()
![]() ,所以B=30°或B=150°.
,所以B=30°或B=150°.
(Ⅱ)![]()
因为0<B<π,所以2sinB的最大值为2,
所以![]()
